浙教版2019-2020学年初中数学七年级下学期期末复习专题1 平行线
试卷更新日期:2020-07-10 类型:复习试卷
一、单选题
-
1. 三条直线a、b、C,若a∥c,b∥c,则a与b的位置关系是( )A、a⊥b B、a∥b C、a⊥b或a∥b D、无法确定2. 下面四个图形中, 与 是同位角的是( )A、
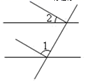 B、
B、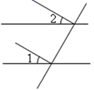 C、
C、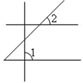 D、
D、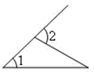 3. 如图,两条直线l1 , l2被第三条直线l3所截,其中一对同位角是( )
3. 如图,两条直线l1 , l2被第三条直线l3所截,其中一对同位角是( ) A、∠1与∠4 B、∠2与∠4 C、∠3与∠4 D、∠1与∠34. 如图,下列条件中,不能判定 的是( )
A、∠1与∠4 B、∠2与∠4 C、∠3与∠4 D、∠1与∠34. 如图,下列条件中,不能判定 的是( ) A、 B、 C、 D、5. 如图1是画平行线时,采用推三角尺的方法从如图1到如图2得到平行线,在平移三角尺画平行线的过程中,使用的数学原理是( )
A、 B、 C、 D、5. 如图1是画平行线时,采用推三角尺的方法从如图1到如图2得到平行线,在平移三角尺画平行线的过程中,使用的数学原理是( ) A、同位角相等,两直线平行 B、两直线平行,内错角相等 C、两直线平行,同位角相等 D、内错角相等,两直线平行6. 如图,直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数是( )
A、同位角相等,两直线平行 B、两直线平行,内错角相等 C、两直线平行,同位角相等 D、内错角相等,两直线平行6. 如图,直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数是( )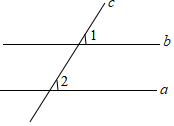 A、120° B、60° C、45° D、30°7. 如图,直线 //b,下列各角中与 相等的是( )
A、120° B、60° C、45° D、30°7. 如图,直线 //b,下列各角中与 相等的是( ) A、 B、 C、 D、8. 下列说法一定正确的是( )A、若直线 , ,则 B、一条直线的平行线有且只有一条 C、若两条线段不相交,则它们互相平行 D、两条不相交的直线叫做平行线9. 在同一平面内,若三条直线 同时满足 则 的关系是( )A、平行 B、垂直 C、相交 D、垂直或平行10. 如图是一块断尺,一块等腰直角三角板的直角顶点刚好落在断尺的下端.则下列结论中,不正确的是( )
A、 B、 C、 D、8. 下列说法一定正确的是( )A、若直线 , ,则 B、一条直线的平行线有且只有一条 C、若两条线段不相交,则它们互相平行 D、两条不相交的直线叫做平行线9. 在同一平面内,若三条直线 同时满足 则 的关系是( )A、平行 B、垂直 C、相交 D、垂直或平行10. 如图是一块断尺,一块等腰直角三角板的直角顶点刚好落在断尺的下端.则下列结论中,不正确的是( ) A、∠1+∠3=90° B、∠5﹣∠2=90° C、∠2+∠3+∠4+∠5=270° D、∠5﹣∠3=90°11. 如图,将△ABC沿射线AB平移到△DEF的位置,则以下结论不正确的是( )
A、∠1+∠3=90° B、∠5﹣∠2=90° C、∠2+∠3+∠4+∠5=270° D、∠5﹣∠3=90°11. 如图,将△ABC沿射线AB平移到△DEF的位置,则以下结论不正确的是( )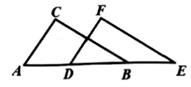 A、∠C=∠F B、BC∥EF C、AD=BE D、AC=DB12. 如图,将△ABC沿着某一方向平移一定的距离得到△DEF,则下列结论:
A、∠C=∠F B、BC∥EF C、AD=BE D、AC=DB12. 如图,将△ABC沿着某一方向平移一定的距离得到△DEF,则下列结论:①AD=CF;②AC∥DF;③∠ABC=∠DFE;④∠DAE=∠AEB.正确的个数为( )
 A、4个 B、3个 C、2个 D、1个13. 如图,能判断 的条件是( )
A、4个 B、3个 C、2个 D、1个13. 如图,能判断 的条件是( ) A、 B、 C、 D、14. 如图,直线l∥m∥n,三角形ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹的角为25°,且∠ACB=60°,则∠a的度数为( )
A、 B、 C、 D、14. 如图,直线l∥m∥n,三角形ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹的角为25°,且∠ACB=60°,则∠a的度数为( ) A、25° B、30° C、35° D、45°15. 已知:如图,点D是射线AB上一动点,连接CD,过点D作DE∥BC交直线AC于点E,若∠ABC=84°,∠CDE=20°,则∠ADC的度数为( )
A、25° B、30° C、35° D、45°15. 已知:如图,点D是射线AB上一动点,连接CD,过点D作DE∥BC交直线AC于点E,若∠ABC=84°,∠CDE=20°,则∠ADC的度数为( )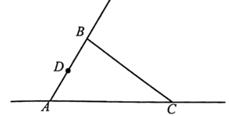 A、104° B、76° C、104°或64° D、104°或76°
A、104° B、76° C、104°或64° D、104°或76°二、填空题
-
16. 如图,点E在BC的延长线上,要使AB∥CD , 需要添加的一个条件是 .
 17. 如图,把一块含有45°角的直角三角板的两个顶点放在真尺的对边上,如果∠1=20°,那么∠2的度数是。
17. 如图,把一块含有45°角的直角三角板的两个顶点放在真尺的对边上,如果∠1=20°,那么∠2的度数是。 18. 如图,将周长为15cm的△ABC沿射线BC方向平移2cm后得到△DEF,则四边形ABFD的周长为cm.
18. 如图,将周长为15cm的△ABC沿射线BC方向平移2cm后得到△DEF,则四边形ABFD的周长为cm.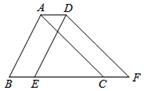 19. 平面内两两相交的三条直线,如果它们最多有a个交点,最少有b个交点,则a+b= .20. 如图,与∠A 是同旁内角的角共有个.
19. 平面内两两相交的三条直线,如果它们最多有a个交点,最少有b个交点,则a+b= .20. 如图,与∠A 是同旁内角的角共有个.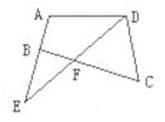
三、解答题
-
21. 如图所示,在∠AOB内有一点P.

①过P画L1∥OA;
②过P画L2∥OB;
③用量角器量一量L1与L2相交的角与∠O的大小有怎样关系?22. 如图: (1)、如果∠1= , 那么DE∥AC,理由: .(2)、如果∠1= , 那么EF∥BC,理由: .(3)、如果∠FED+∠EFC=180°,那么 , 理由: .(4)、如果∠2+∠AED=180°,那么 , 理由: .23. 如图,∠BAC=100°,在∠BAC的内部有一点P,以P为顶点,作∠EPF,使∠EPF的两边与∠BAC的两边分别平行。
(1)、如果∠1= , 那么DE∥AC,理由: .(2)、如果∠1= , 那么EF∥BC,理由: .(3)、如果∠FED+∠EFC=180°,那么 , 理由: .(4)、如果∠2+∠AED=180°,那么 , 理由: .23. 如图,∠BAC=100°,在∠BAC的内部有一点P,以P为顶点,作∠EPF,使∠EPF的两边与∠BAC的两边分别平行。 (1)、请分别在图1、图2中画出2个符合条件的∠EPF(要求所画的两个角的度数不相等)(2)、直接写出所画的∠EPF的度数:图1中∠EPF= ,图2中∠EPF= 。24. 如图,在 网格中,已知△ABC,请按下列要求画格点三角形 (三角形的三个顶点都是小正方形的顶点).
(1)、请分别在图1、图2中画出2个符合条件的∠EPF(要求所画的两个角的度数不相等)(2)、直接写出所画的∠EPF的度数:图1中∠EPF= ,图2中∠EPF= 。24. 如图,在 网格中,已知△ABC,请按下列要求画格点三角形 (三角形的三个顶点都是小正方形的顶点).
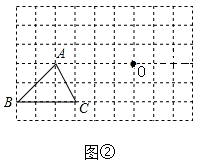 (1)、在图①中,将△ABC平移,使点O落在△ABC的边AB(不包括点A和点B)上;(2)、在图②中,将△ABC平移,使点O落在△ABC的内部.25. 如图,已知AC⊥AE,BD⊥BF,∠1=∠2,求证:AE∥BF.
(1)、在图①中,将△ABC平移,使点O落在△ABC的边AB(不包括点A和点B)上;(2)、在图②中,将△ABC平移,使点O落在△ABC的内部.25. 如图,已知AC⊥AE,BD⊥BF,∠1=∠2,求证:AE∥BF. 26.(1)、请根据所给图形回答下列问题:若∠DEC+∠ACB=180°,可以得到哪两条线段平行?为什么?
26.(1)、请根据所给图形回答下列问题:若∠DEC+∠ACB=180°,可以得到哪两条线段平行?为什么?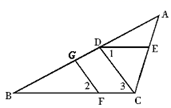 (2)、在(1)中的结论下,如果∠1=∠2,CD⊥AB , 写出FG与AB的位置关系;并给予证明.27.(1)、问题发现:如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC。
(2)、在(1)中的结论下,如果∠1=∠2,CD⊥AB , 写出FG与AB的位置关系;并给予证明.27.(1)、问题发现:如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC。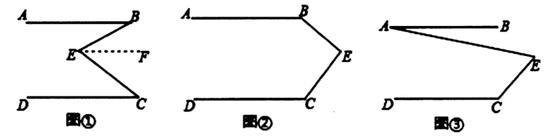
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法).
∴EF∥DC()。
∴∠C=∠CEF()
∵EF∥AB,∴∠B=∠BEF(同理)。
∴∠B+∠C=。
即∠B+∠C=∠BEC。
(2)、拓展探究:如果点E运动到图②所示的位置,其他条件不变,进一步探究发现:∠B+∠C=360°-∠BEC,请说明理由。(3)、解决问题:如图③,AB∥DC,∠C=120°,∠AEC=80°,请直接写出∠A的度数。