北京市燕山地区2020年中考数学二模试卷
试卷更新日期:2020-07-09 类型:中考模拟
一、单选题
-
1. 2020年5月5日18时,长征五号B运载火箭首飞成功,标志着我国空间站工程建设进入实质阶段.长征五号B运载火箭运载能力超过22000克,是目前我国近地轨道运载能力最大的火箭,将22000科学记数法表示应为( )A、 B、 C、 D、2. 如图,用三角板作 的边 上的高线,下列三角板的摆放位置正确的是( )A、
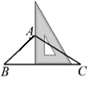 B、
B、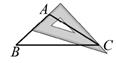 C、
C、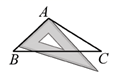 D、
D、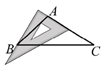 3. 下列防控疫情的图标中,既是轴对称图形,又是中心对称图形的是( )A、
3. 下列防控疫情的图标中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图是某几何体的展开图,则该几何体是( )
4. 如图是某几何体的展开图,则该几何体是( )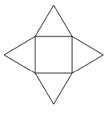 A、四棱锥 B、三棱锥 C、四棱柱 D、长方体5. 如图,在数轴上,实数a,b的对应点分别为点 ,则 ( )
A、四棱锥 B、三棱锥 C、四棱柱 D、长方体5. 如图,在数轴上,实数a,b的对应点分别为点 ,则 ( )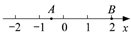 A、1.5 B、1 C、-1 D、-46. 2019年10月20日,第六届世界互联网大会在浙江乌镇举行,会议发布了15项“世界互联网领先科技成果”,其中有5项成果属于芯片领域.小飞同学要从这15项“世界互联网领先科技成果”中任选1项进行了解,则他恰好选中芯片领域成果的概率为( )A、 B、 C、 D、7. 若 ,则代数式 的值为( )A、1 B、2 C、4 D、68. “实际平均续航里程”是指电动汽车的行驶总里程与充电次数的比值,是反映电动汽车性能的重要指标.某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程”,收集了使用该型号电动汽车1年以上的部分客户的相关数据,按年龄不超过40岁和年龄在40岁以上将客户分为 两组,从 组各抽取10位客户的电动汽车的“实际平均续航里程”数据整理成下图,其中“⊙”表示 组的客户,“*”表示 组的客户.
A、1.5 B、1 C、-1 D、-46. 2019年10月20日,第六届世界互联网大会在浙江乌镇举行,会议发布了15项“世界互联网领先科技成果”,其中有5项成果属于芯片领域.小飞同学要从这15项“世界互联网领先科技成果”中任选1项进行了解,则他恰好选中芯片领域成果的概率为( )A、 B、 C、 D、7. 若 ,则代数式 的值为( )A、1 B、2 C、4 D、68. “实际平均续航里程”是指电动汽车的行驶总里程与充电次数的比值,是反映电动汽车性能的重要指标.某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程”,收集了使用该型号电动汽车1年以上的部分客户的相关数据,按年龄不超过40岁和年龄在40岁以上将客户分为 两组,从 组各抽取10位客户的电动汽车的“实际平均续航里程”数据整理成下图,其中“⊙”表示 组的客户,“*”表示 组的客户.下列推断错误的是( )
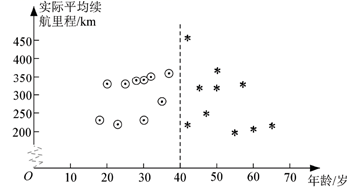 A、A组客户的电动汽车的“实际平均续航里程”的最大值低于B组 B、A组客户的电动汽车的“实际平均续航里程”的方差低于B组 C、A组客户的电动汽车的“实际平均续航里程”的平均值低于B组 D、这20位客户的电动汽车的“实际平均续航里程”的中位数落在B组
A、A组客户的电动汽车的“实际平均续航里程”的最大值低于B组 B、A组客户的电动汽车的“实际平均续航里程”的方差低于B组 C、A组客户的电动汽车的“实际平均续航里程”的平均值低于B组 D、这20位客户的电动汽车的“实际平均续航里程”的中位数落在B组二、填空题
-
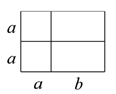
9. 函数y= 中,自变量x的取值范围是;实数2﹣ 的倒数是 .10. 分解因式: =11. 下图中的四边形均为矩形,根据图形的面积关系,写出一个正确的等式: .
 12. 用一个a的值说明命题“若 ,则 ”是假命题,这个值可以是 .13. 如图, 均是五边形 的外角, ,则 °.
12. 用一个a的值说明命题“若 ,则 ”是假命题,这个值可以是 .13. 如图, 均是五边形 的外角, ,则 °.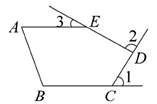 14. 如图,边长为1的小正方形网格中,点 均在格点上,半径为2的 与 交于点F,则 .
14. 如图,边长为1的小正方形网格中,点 均在格点上,半径为2的 与 交于点F,则 .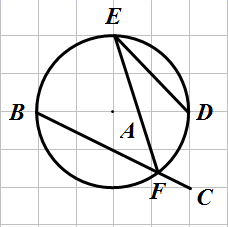 15. 《算法统宗》是中国古代数学名著,作者是明代数学家程大位.其中有一个“绳索量竿”问题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,问索长几尺”.
15. 《算法统宗》是中国古代数学名著,作者是明代数学家程大位.其中有一个“绳索量竿”问题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,问索长几尺”.译文:现有一根杆和一条绳索,用绳索去量杄,绳索比杆子长5尺;如果将绳索对折后再去量竿,就比竿子短5尺,问绳索长几尺?注:一托 尺
设绳索长X尺,竿子长y尺,依题意,可列方程组为 .
16. 四边形 的对角线 交点O,点 分别为边 的中点.有下列四个推断,①对于任意四边形 ,四边形 都是平行四边形;
②若四边形 是平行四边形,则 与 交于点O;
③若四边形 是矩形,则四边形 也是矩形;
④若四边形 是正方形,则四边形 也一定是正方形.
所有符合题意推断的序号是 .
三、解答题
-
17. 计算: .18. 解不等式 ,并把它的解集在数轴上表示出来.
 19. 如图, 中, 于点 的平分线 交 于点E.
19. 如图, 中, 于点 的平分线 交 于点E.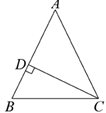 (1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、求证: .20. 已知关于x的方程 .(1)、求证:方程总有两个实数根;(2)、若方程的两个根均为正整数,写出一个满足条件的m的值,并求此时方程的根.21. 如图, 中, 为 中点,O为 中点,连结 并延长到点E,使 ,连接 .
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、求证: .20. 已知关于x的方程 .(1)、求证:方程总有两个实数根;(2)、若方程的两个根均为正整数,写出一个满足条件的m的值,并求此时方程的根.21. 如图, 中, 为 中点,O为 中点,连结 并延长到点E,使 ,连接 .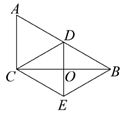 (1)、求证:四边形 为菱形;(2)、若 ,求四边形 的面积.22. 如图,在平面直角坐标系 中,直线 与 轴交于点 ,与反比例函数 的图象交于点 和点B.
(1)、求证:四边形 为菱形;(2)、若 ,求四边形 的面积.22. 如图,在平面直角坐标系 中,直线 与 轴交于点 ,与反比例函数 的图象交于点 和点B.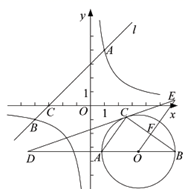 (1)、求 的值及点C的坐标;(2)、若点 是 轴上一点,且 ,直接写出点P的坐标.23. 如图, 为 的直径,点C在 上,过点 作 切线 交 的延长线于点D,过点O作 交切线 于点E,交 于点F.
(1)、求 的值及点C的坐标;(2)、若点 是 轴上一点,且 ,直接写出点P的坐标.23. 如图, 为 的直径,点C在 上,过点 作 切线 交 的延长线于点D,过点O作 交切线 于点E,交 于点F.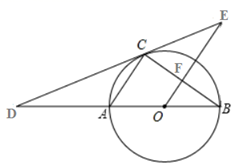 (1)、求证: ;(2)、若 ,求 的长.24. 已知 均是x的函数,下表是 与 的几组对应值.
(1)、求证: ;(2)、若 ,求 的长.24. 已知 均是x的函数,下表是 与 的几组对应值.
小聪根据学习函数的经验,利用上述表格所反映出的 与x之间的变化规律,分别对函数 的图象与性质进行了探究.
下面是小聪的探究过程,请补充完整:
(1)、如图,在同一平面直角坐标系 中,描出上表中各组数值所对应的点 ,并画出函数 的图象;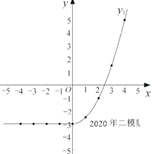 (2)、结合画出的函数图象,解决问题:
(2)、结合画出的函数图象,解决问题:①当 时,对应的函数值 约为;
②写出函数 的一条性质:;
③当 时, 的取值范围是 .
25. 某学校八、九年级各有学生200人,为了提高学生的身体素质,学校开展了主题为“快乐运动,健康成长”的系列体育健身活动.为了了解学生的运动状况,从八、九年级各随机抽取40名学生进行了体能测试,获得了他们的成缋(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.(说明:成绩80分及以上为优秀,70-79分为良好,60-69分为合格,60分以下为不合格)a.八年级学生成绩的频数分布直方图如下(数据分为五组: )
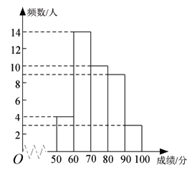
b.八年级学生成绩在 这一组的是:
70 71 73 73 73 74 76 77 78 79
c.九年级学生成绩的平均数、中位数、众数、优秀率如下:
平均数
中位数
众数
优秀率
79
76
84
40%
根据以上信息,回答下列问题:
(1)、在此次测试中,小腾的成绩是74分,在年级排名是第17名,由此可知他是年级的学生(填“八”,或“九”);(2)、根据上述信息,推断年级学生运动状况更好,理由为;(至少从两个不同的角度说明推断的合理性)(3)、假设八、九年级全体学生都参加了此次测试,①预估九年级学生达到优秀的约有人;
②如果年级排名在前70名的学生可以被评选为“运动达人”,预估八年级学生至少要达到分才可以入选.
26. 在平面直角坐标系 中,抛物线 与 轴交于点 (A在B的左侧). (1)、求点 的坐标及抛物线的对称轴;(2)、已知点 ,若抛物线与线段 有公共点,请结合函数图象,求a的取值范围.27. 已知菱形 中, ,点 为边 上一个动点(不与点 重合),点F在边 上,且 ,将线段 绕着点D逆时针旋转120°得线段 ,连接 .
(1)、求点 的坐标及抛物线的对称轴;(2)、已知点 ,若抛物线与线段 有公共点,请结合函数图象,求a的取值范围.27. 已知菱形 中, ,点 为边 上一个动点(不与点 重合),点F在边 上,且 ,将线段 绕着点D逆时针旋转120°得线段 ,连接 .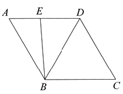 (1)、依题意补全图形;(2)、求证: 为等边三角形(3)、用等式表示线段 的数量关系,并证明.28. 对于平面直角坐标系 中的点P和图形G,给出如下定义:若图形G上存在两个点 ,使得 是边长为2的等边三角形,则称点P是图形G的一个“和谐点”.
(1)、依题意补全图形;(2)、求证: 为等边三角形(3)、用等式表示线段 的数量关系,并证明.28. 对于平面直角坐标系 中的点P和图形G,给出如下定义:若图形G上存在两个点 ,使得 是边长为2的等边三角形,则称点P是图形G的一个“和谐点”.已知直线 与 轴交于点M,与y轴交于点 的半径为r.
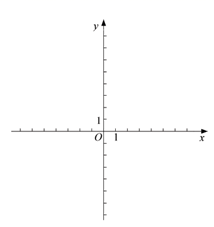 (1)、若 ,在点 中,直线l的和谐点是;(2)、若 上恰好存在2个直线l的和谐点,求n的取值范围;(3)、若 ,线段 上存在 的和谐点,直接写出r的取值范围.
(1)、若 ,在点 中,直线l的和谐点是;(2)、若 上恰好存在2个直线l的和谐点,求n的取值范围;(3)、若 ,线段 上存在 的和谐点,直接写出r的取值范围.