北京市顺义区2020年中考数学二模试卷

试卷更新日期：2020-07-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图所示， $l_{1}$ ∥ $l_{2}$ ，则平行线 $l_{1}$ 与 $l_{2}$ 间的距离是（）

A、线段AB的长度 B、线段BC的长度 C、线段CD的长度 D、线段DE的长度

查看试题解析
2. -5的倒数是（）

A、-5 B、5 C、 $\frac{1}{5}$ D、 $- \frac{1}{5}$

查看试题解析
3. 如图，平面直角坐标系xOy中，有A、B、C、D四点．若有一直线l经过点 $(- 1 ， 3)$ 且与y轴垂直，则l也会经过的点是（）

A、点A B、点B C、点C D、点D

查看试题解析
4. 如果a²+4a-4＝0，那么代数式 $(a - 2) {}^{2}+ 4 (2 a - 3) + 1$ 的值为（）

A、13 B、-11 C、3 D、-3

查看试题解析
5. 如图，四边形 $A B C D$ 中，过点A的直线l将该四边形分割成两个多边形，若这两个多边形的内角和分别为 $α$ 和 $β$ ，则 $α + β$ 的度数是（）

A、 $360 °$ B、 $540 °$ C、 $720 °$ D、 $900 °$

查看试题解析
6. 《九章算术》是中国古代重要的数学著作，其中“盈不足术”记载：今有共买鸡，人出九，盈十一；人出六，不足十六．问人数鸡价各几何？译文：今有人合伙买鸡，每人出九钱，会多出11钱；每人出6钱，又差16钱．问人数、买鸡的钱数各是多少？设人数为 $x$ ，买鸡的钱数为 $y$ ，可列方程组为（）

A、 ${\begin{matrix} 9 x + 11 = y \\ 6 x + 16 = y \end{matrix}$ B、 ${\begin{matrix} 9 x - 11 = y \\ 6 x - 16 = y \end{matrix}$ C、 ${\begin{matrix} 9 x + 11 = y \\ 6 x - 16 = y \end{matrix}$ D、 ${\begin{matrix} 9 x - 11 = y \\ 6 x + 16 = y \end{matrix}$

查看试题解析
7. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵，每棵产量的平均数x（单位：千克）及方差S²（单位：千克²）如下表所示：

甲

乙

丙

丁

x

24

24

23

20

S²

2.1

1.9

2

1.9

今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 正方形 $A B C D$ 的边 $A B$ 上有一动点E，以 $E C$ 为边作矩形 $E C F G$ ，且边 $F G$ 过点 $D$ ．设AE=x ，矩形 $E C F G$ 的面积为y ，则y与x之间的关系描述正确的是（）

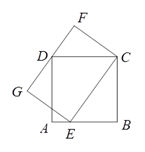A、y与x之间是函数关系，且当x增大时，y先增大再减小 B、y与x之间是函数关系，且当x增大时，y先减小再增大 C、y与x之间是函数关系，且当x增大时，y一直保持不变 D、y与x之间不是函数关系

查看试题解析

二、填空题

9. 分解因式： $2 m n^{2} - 2 m$ = ．

查看试题解析
10.
如图中的四边形均为矩形，根据图形，写出一个正确的等式.

查看试题解析
11. 比较大小： $\frac{\sqrt{5} - 1}{2}$ 0.5．（填“>”“<”或“=”）

查看试题解析
12. 如图，在每个小正方形的边长为1cm的网格中，画出了一个过格点A ， B的圆，通过测量、计算，求得该圆的周长是 cm．（结果保留一位小数）

查看试题解析
13. 如图， $∠ M A N = 30 °$ ，点 $B$ 在射线 $A M$ 上，且 $A B = 2$ ，则点 $B$ 到射线 $A N$ 的距离是．

查看试题解析
14. 如图，Rt△ABC中，∠C=90°，在△ABC外取点D ， E ，使AD=AB ， AE=AC ，且α+β＝∠B ，连结DE ．若AB＝4，AC＝3，则DE＝．

查看试题解析
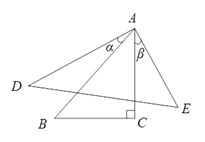15. 数学活动课上，老师拿来一个不透明的袋子，告诉学生里面装有4个除颜色外均相同的小球，并且球的颜色为红色和白色，让学生通过多次有放回的摸球，统计摸出红球和白球的次数，由此估计袋中红球和白球的个数．下面是全班分成的三个小组各摸球20次的结果，请你估计袋中有个红球．

摸到红球的次数

摸到白球的次数

一组

13

7

二组

14

6

三组

15

5

查看试题解析
16. 对于题目：“如图1，平面上，正方形内有一长为12 、宽为6 的矩形，它可以在正方形的内部及边界通过移转（即平移或旋转）的方式，自由地从横放移转到竖放，求正方形边长的最小整数 $n$ ．”甲、乙、丙作了自认为边长最小的正方形，先求出该边长 $x$ ，再取最小整数 $n$ ．
甲：如图2，思路是当 $x$ 为矩形对角线长时就可移转过去；结果取n=14．

乙：如图3，思路是当 $x$ 为矩形外接圆直径长时就可移转过去；结果取n=14．

丙：如图4，思路是当 $x$ 为矩形的长与宽之和的 $\frac{\sqrt{2}}{2}$ 倍时就可移转过去；结果取n=13．

甲、乙、丙的思路和结果均正确的是．

查看试题解析

三、解答题

17. 计算： ${(- 2)}^{0} + \sqrt{\frac{1}{2}} - \cos 45 ° - 3^{- 2}$ ．

查看试题解析
18. 解不等式： $\frac{x - 1}{3}$ ≥ $\frac{x - 2}{2} + 1$ ，并把解集在数轴上表示出来．

查看试题解析
19. 已知：关于x的方程 $m x^{2} - 4 x + 1 = 0 (m \neq 0)$ 有实数根．

(1)、求m的取值范围；

(2)、若方程的根为有理数，求正整数m的值．

查看试题解析
20. 下面是小东设计的“以线段AB为一条对角线作一个菱形”的尺规作图过程．
已知：线段AB．

求作：菱形ACBD．

作法：如图，

①以点A为圆心，以AB长为半径作⊙A；

②以点 B为圆心，以AB长为半径作⊙B，

交⊙A 于C，D两点；

③连接AC，BC，BD，AD．

所以四边形ACBD就是所求作的菱形．

根据小东设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：∵点B，C，D在⊙A上，

∴AB=AC=AD(      ▲       )（填推理的依据）．

同理 ∵点A，C，D在⊙B上，

∴AB=BC=BD．

∴    ▲    =   ▲    =   ▲    =    ▲    ．

∴四边形ACBD是菱形． (     ▲     )（填推理的依据）．

查看试题解析
21. 已知：如图，在四边形ABCD中， $∠ B A C = ∠ A C D = 90 °$ ， $A B = \frac{1}{2} C D$ ，点E是CD的中点．

(1)、求证：四边形ABCE是平行四边形；

(2)、若 $A C = 4$ ， $A D = 4 \sqrt{2}$ ，求四边形ABCE的面积．

查看试题解析
22. 为了研究一种新药的疗效，选100名患者随机分成两组，每组各50名，一组服药，另一组不服药，12周后，记录了两组患者的生理指标 $x$ 和 $y$ 的数据，并制成下图，其中“*”表示服药者，“+”表示未服药者；

同时记录了服药患者在4周、8周、12周后的指标z的改善情况，并绘制成条形统计图．

根据以上信息，回答下列问题：

(1)、从服药的50名患者中随机选出一人，求此人指标 $x$ 的值大于1.7的概率；

(2)、设这100名患者中服药者指标 $y$ 数据的方差为 $S_{1}^{2}$ ，未服药者指标 $y$ 数据的方差为 $S_{2}^{2}$ ，则 $S_{1}^{2}$ $S_{2}^{2}$ ；（填“>”、“=”或“<” ）

(3)、对于指标z的改善情况，下列推断合理的是．
①服药4周后，超过一半的患者指标z没有改善，说明此药对指标z没有太大作用；

②在服药的12周内，随着服药时间的增长，对指标z的改善效果越来越明显．

查看试题解析
23. 已知：如图，AB是⊙O的直径，△ABC内接于⊙O ．点D在⊙O上，AD平分∠CAB交BC于点E ， DF是⊙O的切线，交AC的延长线于点F ．

(1)、求证；DF⊥AF；

(2)、若⊙O的半径是5， AD=8，求DF的长．

查看试题解析

24. 如图，在

Δ A B C

中，

A B = A C = 5

cm，

B C = 6

cm，点

D

为

B C

的中点，点E为AB的中点．点

M

为AB边上一动点，从点B出发，运动到点A停止，将射线DM绕点

D

顺时针旋转

α

度（其中

α = ∠ B D E

），得到射线DN ， DN与边AB或AC交于点N ．设

B

、

M

两点间的距离为

x

cm，

M

，

N

两点间的距离为

y

cm．

小涛根据学习函数的经验，对函数 $y$ 随自变量 $x$ 的变化而变化的规律进行了探究．

下面是小涛的探究过程，请补充完整．

(1)、列表：按照下表中自变量x的值进行取点、画图、测量，分别得到了

y

与

x

的几组对应值：

x/cm	0	0.3	0.5	1.0	1.5	1.8	2.0	2.5	3.0	3.5	4.0	4.5	4.8	5.0
y/cm	2.5	2.44	2.42	2.47	2.79		2.94	2.52	2.41	2.48	2.66	2.9	3.08	3.2

请你通过测量或计算，补全表格；

(2)、描点、连线：在平面直角坐标系

x O y

中，描出补全后的表格中各组数值所对应的点

(x ， y)

，并画出函数y关于x的图象．

(3)、结合函数图象，解决问题：当

M N = B D

时，

B M

的长度大约是cm．（结果保留一位小数）

查看试题解析

25. 已知：在平面直角坐标系xOy中，点A（-1，2）在函数 $y = \frac{m}{x}$ (x<0)的图象上．

(1)、求m的值；

(2)、过点A作y轴的平行线 $l$ ，直线 $y = - 2 x + b$ 与直线 $l$ 交于点B ，与函数 $y = \frac{m}{x}$ (x<0)的图象交于点C ，与 $y$ 轴交于点D ．
①当点C是线段BD的中点时，求b的值；

②当BC<BD时，直接写出b的取值范围．

查看试题解析
26. 在平面直角坐标系xOy中，已知抛物线 $y = m x^{2} - 3 (m - 1) x + 2 m - 1 (m \neq 0)$ ．

(1)、当m=3时，求抛物线的顶点坐标；

(2)、已知点A(1，2)．试说明抛物线总经过点A；

(3)、已知点B(0，2)，将点B向右平移3个单位长度，得到点C ，若抛物线与线段BC只有一个公共点，求m的取值范围．

查看试题解析
27. 已知：在△ABC中，∠ABC=90°，AB=BC ，点D为线段BC上一动点（点D不与点B、C重合），点B关于直线AD的对称点为E ，作射线DE ，过点C作BC的垂线，交射线DE于点F ，连接AE ．

(1)、依题意补全图形；

(2)、AE与DF的位置关系是；

(3)、连接AF ，小昊通过观察、实验，提出猜想：发现点D 在运动变化的过程中，∠DAF的度数始终保持不变，小昊把这个猜想与同学们进行了交流，经过测量，小昊猜想∠DAF=°，通过讨论，形成了证明该猜想的两种想法：
想法1：过点A作AG⊥CF于点G ，构造正方形ABCG ，然后可证△AFG≌△AFE……

想法2：过点B作BG∥AF ，交直线FC于点G ，构造□ABGF ，然后可证△AFE≌△BGC……

请你参考上面的想法，帮助小昊完成证明（一种方法即可）．

查看试题解析
28. 已知：如图，⊙O的半径为r ，在射线OM上任取一点P（不与点O重合），如果射线OM上的点P' ，满足OP·OP'=r² ，则称点P'为点P关于⊙O的反演点．

在平面直角坐标系xOy中，已知⊙O的半径为2．

(1)、已知点A (4，0)，求点A关于⊙O的反演点A'的坐标；

(2)、若点B关于⊙O的反演点B'恰好为直线 $y = \sqrt{3} x$ 与直线x=4的交点，求点B的坐标；

(3)、若点C为直线 $y = \sqrt{3} x$ 上一动点，且点C关于⊙O的反演点C'在⊙O的内部，求点C的横坐标m的范围；

(4)、若点D为直线x=4上一动点，直接写出点D关于⊙O的反演点D'的横坐标t的范围．

查看试题解析

	摸到红球的次数	摸到白球的次数
一组	13	7
二组	14	6
三组	15	5

	甲	乙	丙	丁
x	24	24	23	20
S²	2.1	1.9	2	1.9