北京市平谷区2020年中考数学二模试卷
试卷更新日期:2020-07-09 类型:中考模拟
一、单选题
-
1. 垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 实数a , b , c在数轴上的对应点的位置如图所示,若a与c互为相反数,则a , b , c中绝对值最大的数是( )
2. 实数a , b , c在数轴上的对应点的位置如图所示,若a与c互为相反数,则a , b , c中绝对值最大的数是( )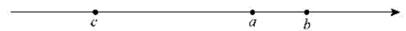 A、a B、b C、c D、无法确定3. 聪聪在阅读一篇文章时看到水分子的直径约为0.4纳米,通过百度搜索聪聪又知道1纳米 米,则水分子的直径约为( )A、 米 B、 米 C、 米 D、 米4. 下列几何体中主视图为矩形的是( )A、
A、a B、b C、c D、无法确定3. 聪聪在阅读一篇文章时看到水分子的直径约为0.4纳米,通过百度搜索聪聪又知道1纳米 米,则水分子的直径约为( )A、 米 B、 米 C、 米 D、 米4. 下列几何体中主视图为矩形的是( )A、 B、
B、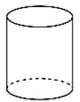 C、
C、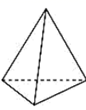 D、
D、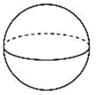 5. 如果 ,那么代数式 的值为( )A、 B、-2 C、 D、26. 如图,螺丝母的截面是正六边形,则 的度数为( )
5. 如果 ,那么代数式 的值为( )A、 B、-2 C、 D、26. 如图,螺丝母的截面是正六边形,则 的度数为( ) A、30° B、45° C、60° D、75°7. 某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位: )如下图所示:
A、30° B、45° C、60° D、75°7. 某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位: )如下图所示:
设两队队员身高的平均数依次为 ,方差依次为 ,下列关系中完全正确的是( )
A、 B、 C、 D、8. 如图,是某企业甲、乙两位员工的能力测试结果的网状图,以O为圆心的五个同心圆分别代表能力水平的五个等级由低到高分别赋分1至5分,由原点出发的五条线段分别指向能力水平的五个维度,网状图能够更加直观的描述测试者的优势和不足,观察图形,有以下几个推断: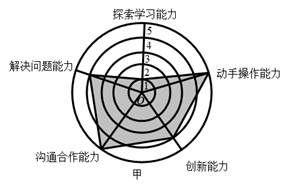
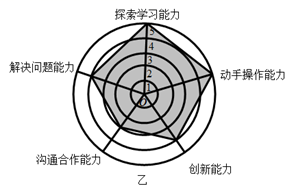
①甲和乙的动手操作能力都很强;②缺少探索学习的能力是甲自身的不足;③与甲相比乙需要加强与他人的沟通合作能力;④乙的综合评分比甲要高.其中合理的是( )
A、①③ B、②④ C、①②③ D、①②③④二、填空题
-
9. 因式分解:x2y﹣9y= .
10. 如图所示,边长为1正方形网格中,点A、B、C落在格点上,则 的度数为 .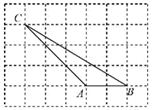 11. 如果二次根式 有意义,那么x的取值范围是 .12. 如图,直线 ,点A、B是直线l上两点,点C、D是直线m上两点,连接 . 交于点O , 设 的面积为 , 的面积为 ,则 .(填“>”,“<”或“=”)
11. 如果二次根式 有意义,那么x的取值范围是 .12. 如图,直线 ,点A、B是直线l上两点,点C、D是直线m上两点,连接 . 交于点O , 设 的面积为 , 的面积为 ,则 .(填“>”,“<”或“=”)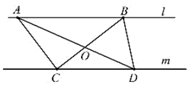 13. 若一次函数的图象过点(0,2),且函数y随自变量x的增大而增大,请写出一个符合要求的一次函数表达式: .14. 用一个a的值说明命题“ 一定表示一个负数”是错误的,a的值可以是 .15. 图1中的小矩形长为x , 宽为y , 将四个同样的小矩形拼成如图2的正方形,则可列出关于x , y的方程组为 .
13. 若一次函数的图象过点(0,2),且函数y随自变量x的增大而增大,请写出一个符合要求的一次函数表达式: .14. 用一个a的值说明命题“ 一定表示一个负数”是错误的,a的值可以是 .15. 图1中的小矩形长为x , 宽为y , 将四个同样的小矩形拼成如图2的正方形,则可列出关于x , y的方程组为 .
 16. 某商场在端午节前以1元/个的价格购进1000个粽子,现有以下三种销售方式:不加工直接卖,对产品进行粗加工后再卖,对产品进行精加工后再卖.受加工能力和气温影响,粗加工一天只能加工200个,细加工一天只能加工100个,两种加工不能同时进行,且最多加工三天.
16. 某商场在端午节前以1元/个的价格购进1000个粽子,现有以下三种销售方式:不加工直接卖,对产品进行粗加工后再卖,对产品进行精加工后再卖.受加工能力和气温影响,粗加工一天只能加工200个,细加工一天只能加工100个,两种加工不能同时进行,且最多加工三天.加工方式
加工成本
销售单位
售价
直接卖
0
个
2元/个
粗加工
1元/个
包装袋(一袋5个)
30元/袋
精加工
2.5元/个
礼盒(一盒10个)
85元/盒
假设所有粽子均能全部售出,则以下销售方式中利润最大的是 .
方案一:不加工直接销售;
方案二:三天全部进行精加工,剩下的直接卖;
方案三:两天精加工,一天粗加工,剩下的直接卖;
方案四:两天粗加工,一天精加工,剩下的直接卖.
三、解答题
-
17. 计算: .18. 解不等式组:19. 下面是小元设计的“过直线外一点作已知直线的平行线”的尺规作图过程.

已知:如图,直线l和直线外一点P .
求作:过点P作直线l的平行线.
作法:如图,
①在直线l上任取点O;
②作直线 ;
③以点O为圆心 长为半径画圆,交直线 于点A , 交直线l于点B;
④连接 ,以点B为圆心, 长为半径画弧,交 于点C(点A与C不重合);
⑤作直线 .
则直线 即为所求.
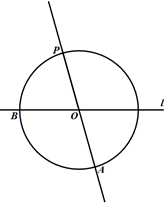
根据小元设计的尺规作图过程,完成以下任务.
(1)、补全图形;(2)、完成下面的证明:证明:连接
∵
∴
∴ ▲ ▲ ,
又∵ ,
∴ ▲ ▲ ,
∴ ,
∴ ( ▲ )(填推理的依据).
20. 已知关于x的一元二次方程 .(1)、求证:方程总有两个实数根;(2)、任意写出一个k值代入方程,并求出此时方程的解.21. 如图,在菱形 中,延长 到E , 延长 到F , 使 ,连接 ,连接 并延长交 于点G .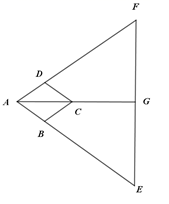 (1)、求证: ;(2)、连接 交 于 ,过B作 于点M , 若 ,C为 中点,求 的长.22. 如图,以 为直径的 ,交 于点E , 过点O作半径 于点G , 连接 交 于点F , 且 .
(1)、求证: ;(2)、连接 交 于 ,过B作 于点M , 若 ,C为 中点,求 的长.22. 如图,以 为直径的 ,交 于点E , 过点O作半径 于点G , 连接 交 于点F , 且 .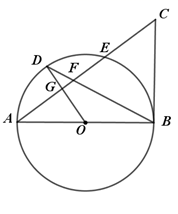 (1)、求证: 是 的切线;(2)、若 的半径为5, ,求 的长.23. 如图,在平面直角坐标系 中,正方形 的边长为2,函数 的图象经过点B , 与直线 交于点D .
(1)、求证: 是 的切线;(2)、若 的半径为5, ,求 的长.23. 如图,在平面直角坐标系 中,正方形 的边长为2,函数 的图象经过点B , 与直线 交于点D .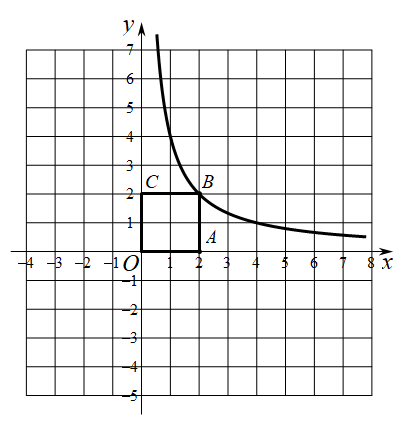 (1)、求k的值;(2)、直线 与 边所在直线交于点M , 与x轴交于点N .
(1)、求k的值;(2)、直线 与 边所在直线交于点M , 与x轴交于点N .①当点D为 中点时,求b的值;
②当 时,结合函数图象,直接写出b的取值范围.
24. 疫情期间某校学生积极观看网络直播课程,为了了解全校500名学生观看网络直播课程的情况,随机抽取50名学生,对他们观看网络直播课程的节数进行收集,并对数据进行了整理、描述和分析,下面给出了部分信息.观看直播课节数的频数分布表
节数x
频数
频率
8
0.16
10
0.20
16
0.24
4
0.08
总数
50
1
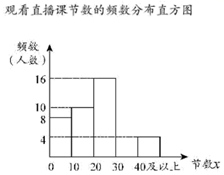
其中,节数在 这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)、 , ;(2)、请补全频数分布直方图;(3)、随机抽取的50名学生观看直播课节数的中位数是;(4)、请估计该校学生中观看网络直播课节数不低于30次的约有人.25. 如图,M是弦 与弧 所围成的图形的内部的一个定点,P是弦 上一动点,连接 并延长交弧 于点Q , 连接 .已知 ,设A , P两点间的距离为 ,P , Q两点间距离为 , 两点间距离为 .
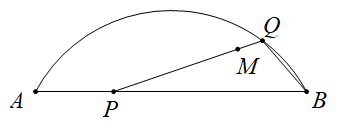
小明根据学习函数的经验,分别对函数 随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
(1)、按照如表中自变量x的值进行取点、画图、测量,分别得到了 与x的几组对应值,补全下表:0
1
2
3
4
5
6
5.24
4.24
3.24
1.54
1.79
3.47
1.31
1.34
1.42
1.54
1.80
2.45
3.47
(2)、在同一平面直角坐标系 中,描出表中各组数值对应的点 和 并画出函数 的图象;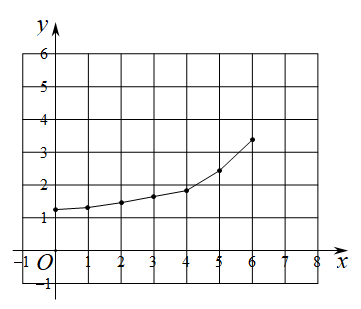 (3)、结合函数图象,解决问题:当 为等腰三角形时, 的长度约 .(精确到0.1)26. 在平面直角坐标系 中,抛物线 与x轴的交点为A , B , 与y轴交于C .
(3)、结合函数图象,解决问题:当 为等腰三角形时, 的长度约 .(精确到0.1)26. 在平面直角坐标系 中,抛物线 与x轴的交点为A , B , 与y轴交于C . (1)、求抛物线的对称轴和点C坐标;(2)、横、纵坐标都是整数的点叫做整点.拋物线在点A , B之间的部分与线段 所围成的区域为图形W(不含边界).
(1)、求抛物线的对称轴和点C坐标;(2)、横、纵坐标都是整数的点叫做整点.拋物线在点A , B之间的部分与线段 所围成的区域为图形W(不含边界).①当 时,求图形W内的整点个数;
②若图形W内有2个整数点,求m的取值范围.
27. 如图,在 中, ,延长 使 ,线段 绕点C顺时针旋转90°得到线段 ,连结 .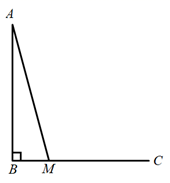 (1)、依据题意补全图形;(2)、当 时, 的度数是;(3)、小聪通过画图、测量发现,当 是一定度数时, .
(1)、依据题意补全图形;(2)、当 时, 的度数是;(3)、小聪通过画图、测量发现,当 是一定度数时, .小聪把这个猜想和同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:通过观察图形可以发现,如果把梯形 补全成为正方形 ,就易证 ,因此易得当 是特殊值时,问题得证;
想法2:要证 ,通过第(2)问,可知只需要证明 是等边三角形,通过构造平行四边形 ,易证 ,通过 ,易证 ,从而解决问题;
想法3:通过 ,连结 ,易证 ,易得 是等腰三角形,因此当 是特殊值时,问题得证.
请你参考上面的想法,帮助小聪证明当 是一定度数时, .(一种方法即可)
28. 如图1,点P是平面内任意一点,点A , B是 上不重合的两个点,连结 .当 时,我们称点P为 的“关于 的关联点”.
 (1)、如图2,当点P在 上时,点P是 的“关于 的关联点”时,画出一个满足条件的 ,并直接写出 的度数;(2)、在平面直角坐标系中有点 ,点M关于y轴的对称点为点N .
(1)、如图2,当点P在 上时,点P是 的“关于 的关联点”时,画出一个满足条件的 ,并直接写出 的度数;(2)、在平面直角坐标系中有点 ,点M关于y轴的对称点为点N .
①以点O为圆心, 为半径画 ,在y轴上存在一点P , 使点P为 “关于 的关联点”,直接写出点P的坐标;
②点 是x轴上一动点,当 的半径为1时,线段 上至少存在一点是 的“关于某两个点的关联点”,求m的取值范围.