北京市密云区2020年中考数学二模试卷

试卷更新日期：2020-07-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 港珠澳大桥作为世界首例集桥梁、隧道和人工岛于一体的超级工程，创下了多项“世界之最”．它是世界上总体跨度最长的跨海大桥，全长55000米．其中海底隧道部分全长6700米，是世界最长的公路沉管隧道和唯一的深埋沉管隧道，也是我国第一条外海沉管隧道．其中，数字6700用科学记数法表示为（）

A、 $67 \times 10^{2}$ B、 $6.7 \times 10^{3}$ C、 $6.7 \times 10^{4}$ D、 $0.67 \times 10^{4}$

查看试题解析
2. 第二十四届冬季奥林匹克运动会将于2022年在北京举行，北京将成为历史上第一座既举办过夏奥会，又举办过冬奥会的城市．下面的图形是各届冬奥会会徽中的部分图案，其中是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，小林利用圆规在线段 $C E$ 上截取线段 $C D$ ，使 $C D = A B$ ．若点D恰好为 $C E$ 的中点，则下列结论中错误的是（）

A、 $C D = D E$ B、 $A B = D E$ C、 $C E = \frac{1}{2} C D$ D、 $C E = 2 A B$

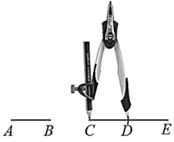查看试题解析
4. 如图所示的四边形均为矩形或正方形，下列等式能够符合题意表示该图形面积关系的是（）

A、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ B、 ${(a + b)}^{2} = a^{2} + 2 a b - b^{2}$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 ${(a - b)}^{2} = a^{2} - 2 a b - b^{2}$

查看试题解析
5. 如图，在数轴上，点B在点A的右侧．已知点A对应的数为 $- 1$ ，点B对应的数为m ．若在 $A B$ 之间有一点C ，点C到原点的距离为2，且 $A C - B C = 2$ ，则m的值为（）

A、4 B、3 C、2 D、1

查看试题解析
6. 如果 $x^{2} + 2 x - 2 = 0$ ，那么代数式 $\frac{1}{x - 2} \cdot \frac{x^{2} - 4 x + 4}{x} - \frac{x}{x + 2}$ 的值为（）

A、 $- 2$ B、-1 C、1 D、2

查看试题解析

7. 新冠疫情发生以来，为保证防控期间的口罩供应，某公司加紧转产，开设多条生产线争分夺秒赶制口罩，从最初转产时的陌生，到正式投产后达成日均生产100万个口罩的产能．不仅效率高，而且口罩送检合格率也不断提升，真正体现了“大国速度”．以下是质监局对一批口罩进行质量抽检的相关数据，统计如下：

抽检数量n/个	20	50	100	200	500	1000	2000	5000	10000
合格数量m/个	19	46	93	185	459	922	1840	4595	9213
口罩合格率 $\frac{m}{n}$	0.950	0.920	0.930	0.925	0.918	0.922	0.920	0.919	0.921

下面四个推断合理的是（）

A、当抽检口罩的数量是10000个时，口罩合格的数量是9213个，所以这批口罩中“口罩合格”的概率是0.921； B、由于抽检口罩的数量分别是50和2000个时，口罩合格率均是0.920，所以可以估计这批口罩中“口罩合格”的概率是0.920； C、随着抽检数量的增加，“口罩合格”的频率总在0.920附近摆动，显示出一定的稳定性，所以可以估计这批口罩中“口罩合格”的概率是0.920； D、当抽检口罩的数量达到20000个时，“口罩合格”的概率一定是0.921．

查看试题解析

8. 如图，点C、A、M、N在同一条直线l上．其中， $△ A B C$ 是等腰直角三角形， $∠ B = 90 °$ ，四边形 $M N P Q$ 为正方形，且 $A C = 4 ， M N = 2$ ，将等腰 $R t △ A B C$ 沿直线l向右平移．若起始位置为点A与点M重合，终止位置为点C与点N重合．设点A平移的距离为x ，两个图形重叠部分的面积为y ，则y与x的函数图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 分解因式： $3 a x^{2} - 12 a =$ ．

查看试题解析
10. 若 $\sqrt{x - 4}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
11. 如图，已知菱形 $A B C D$ ，通过测量、计算得菱形 $A B C D$ 的面积约为 ${cm}^{2}$ ．（结果保留一位小数）

查看试题解析
12. 如图， $∠ 1$ 、 $∠ 2$ 、 $∠ 3$ 、 $∠ 4$ 是五边形 $A B C D E$ 的4个外角，若 $∠ A = 120 °$ ，则 $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 =$ °．

查看试题解析
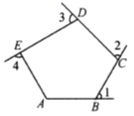13. 已知“若 $a > b$ ，则 $a c < b c$ ”是真命题，请写出一个满足条件的c的值是．

查看试题解析
14. 如图，小军在A时测量某树的影长时，日照的光线与地面的夹角恰好是60°，当他在B时测量该树的影长时，日照的光线与地面的夹角是30°，若两次测得的影长之差 $D E$ 为 $4m$ ，则树的高度为 $m$ ．（结果精确到0.1，参考数据： $\sqrt{2} \approx 1.414 ， \sqrt{3} \approx 1.732$ ）

查看试题解析

15. 已知：点A、点B在直线

M N

的两侧．

（点A到直线 $M N$ 的距离小于点B到直线 $M N$ 的距离）．

如图，

⑴作点B关于直线 $M N$ 的对称点C；

⑵以点C为圆心， $\frac{1}{2} B C$ 的长为半径作 $⊙ C$ ，交 $B C$ 于点E；

⑶过点A作 $⊙ C$ 的切线，交 $⊙ C$ 于点F，交直线 $M N$ 于点P；

⑷连接 $P B$ 、 $P C$ ．

根据以上作图过程及所作图形，下列四个结论中：

① $P E$ 是 $⊙ C$ 的切线； ② $P C$ 平分 $\overset{⌢}{E F}$ ；

③ $P B = P C = P F$ ； ④ $∠ A P N = 2 ∠ B P N$ ．

所有正确结论的序号是．

查看试题解析

16. 某校举办初中生数学素养大赛，比赛共设四个项目：七巧拼图、趣题巧解、数学应用和魔方复原，每个项目得分都按一定百分比折算后记入总分，并规定总分在85分以上（含85分）设为一等奖．下表为甲、乙、丙三位同学的得分情况（单位：分），其中甲的部分信息不小心被涂黑了．

据悉，甲、乙、丙三位同学的七巧拼图和魔方复原两项得分折算后的分数之和均为20分．设趣题巧解和数学应用两个项目的折算百分比分别为x和y ，请用含x和y的二元一次方程表示乙同学“趣题巧解和数学应用”两项得分折算后的分数之和为；如果甲获得了大赛一等奖，那么甲的“数学应用”项目至少获得分．

查看试题解析

三、解答题

17. 计算： $\sqrt[3]{8} - {(\frac{1}{3})}^{- 1} + | 5 - \sqrt{3} | - 6 \tan 30^{°}$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 5 x - 3 \geq 2 x \\ \frac{3 x - 1}{2} < 4 \end{array}$ ．

查看试题解析
19. 在 $▱ A B C D$ 中， $D B = D C ， ∠ C = 70 ° ， A E ⊥ B D$ 于点E ，求 $∠ D A E$ 的度数．

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} + 2 x + m - 4 = 0$ 有两个实数根．

(1)、求m的取值范围；

(2)、写出一个满足条件的m的值，并求出此时方程的根．

查看试题解析
21. 如图，在 $△ A O C$ 中， $O A = O C ， O D$ 是 $A C$ 边中线．延长 $A O$ 至点B，作 $∠ C O B$ 的角平分线 $O H$ ，过点C作 $C F ⊥ O H$ 于点F．

(1)、求证：四边形 $C D O F$ 是矩形；

(2)、连接 $D F$ ，若 $\cos A = \frac{3}{5} ， C F = 8$ ，求 $D F$ 的长．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，直线 $l ： y = x + b$ 与反比例函数 $y = \frac{4}{x}$ 在第一象限内的图象交于点 $A (4 ， m)$ ．

(1)、求m、b的值；

(2)、点B在反比例函数的图象上，且点B的横坐标为1．若在直线l上存在一点P（点P不与点A重合），使得 $A P \leq A B$ ，结合图象直接写出点P的横坐标 $x_{p}$ 的取值范围．

查看试题解析
23. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆， $A B$ 是 $⊙ O$ 的直径，点D在 $⊙ O$ 上， $A C$ 平分 $∠ B A D$ ，过点C的切线交直径 $A B$ 的延长线于点E ，连接 $A D$ 、 $B C$ ．

(1)、求证： $∠ B C E = ∠ C A D$ ；

(2)、若 $A B = 10 ， A D = 6$ ，求 $C E$ 的长．

查看试题解析

24. “垃圾分类就是新时尚”．树立正确的垃圾分类观念，促进青少年养成良好的文明习惯，对于增强公共意识，提升文明素质具有重要意义．为了调査学生对垃圾分类知识的了解情况，从甲、乙两校各随机抽取20名学生进行了相关知识测试，获得了他们的成绩（百分制，单位：分），并对数据（成绩）进行了整理、描述和分析，下面给出了部分信息．

a ．甲、乙两校学生样本成绩频数分布表及扇形统计图如下：

甲校学生样本成绩频数分布表（表1）

成绩m（分）	频数	频率
$50 \leq m < 60$	$a$	0.10
$60 \leq m < 70$	$b$	$c$
$70 \leq m < 80$	4	0.20
$80 \leq m < 90$	7	0.35
$90 \leq m \leq 100$	2	$d$
合计	20	1.0

b ．甲、乙两校学生样本成绩的平均分、中位数、众数、方差如下表所示：（表2）

学校	平均分	中位数	众数	方差
甲	76.7	77	89	150.2
乙	78.1	80	n	135.3

其中，乙校20名学生样本成绩的数据如下：

54 72 62 91 87 69 88 79 80 62 80 84 93 67 87 87 90 71 68 91

请根据所给信息，解答下列问题：

(1)、表1中

c =

；表2中的众数

n =

；

(2)、乙校学生样本成绩扇形统计图（图1）中，

70 \leq m < 80

这一组成绩所在扇形的圆心角度数是度；

(3)、在此次测试中，某学生的成绩是79分，在他所属学校排在前10名，由表中数据可知该学生是校的学生（填“甲”或“乙”），理由是；

(4)、若乙校1000名学生都参加此次测试，成绩80分及以上为优秀，请估计乙校成绩优秀的学生约为人．

查看试题解析

25. 有这样一个问题：探究函数

y = \frac{1}{2} x^{3} - 4 x + 1

的图象与性质．

文文根据学习函数的经验，对函数 $y = \frac{1}{2} x^{3} - 4 x + 1$ 的图象与性质进行了探究．

下面是文文的探究过程，请补充完整：

(1)、函数

y = \frac{1}{2} x^{3} - 4 x + 1

的自变量x的取值范围是；

(2)、下表是y与x的几组对应值：

…

$- 3$

$- 2$

$- \frac{3}{2}$

$- 1$

$- \frac{1}{2}$

$\frac{1}{2}$

$\frac{3}{2}$

…

$- \frac{1}{2}$

$\frac{85}{16}$

$\frac{9}{2}$

$\frac{47}{16}$

$- \frac{15}{16}$

$- \frac{53}{16}$

$- 3$

$\frac{5}{2}$

…

则m的值为；

(3)、如图，在平面直角坐标系

x O y

中，描出以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；

(4)、请你根据探究二次函数与一元二次方程关系的经验，结合图象直接写出方程

\frac{1}{2} x^{3} - 4 x = - 1

的正数根约为．（结果精确到0.1）

查看试题解析

26. 在平面直角坐标系 $x O y$ 中，抛物线 $C_{1} ： y = x^{2} + b x + c$ 与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C ．点B的坐标为 $(3 ， 0)$ ，将直线 $y = k x$ 沿y轴向上平移3个单位长度后，恰好经过B、C两点．

(1)、求k的值和点C的坐标；

(2)、求抛物线 $C_{1}$ 的表达式及顶点D的坐标；

(3)、已知点E是点D关于原点的对称点，若抛物线 $C_{2} ： y = a x^{2} - 2 (a \neq 0)$ 与线段 $A E$ 恰有一个公共点，结合函数的图象，求a的取值范围．

查看试题解析
27. 已知： $M N$ 是经过点A的一条直线，点C是直线 $M N$ 左侧的一个动点，且满足 $60 ° < ∠ C A N < 120 °$ ，连接 $A C$ ，将线段 $A C$ 绕点C顺时针旋转60°，得到线段 $C D$ ，在直线 $M N$ 上取一点B ，使 $∠ D B N = 60 °$ ．

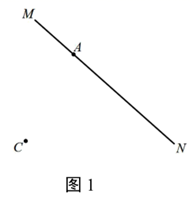
(1)、若点C位置如图1所示．
①依据题意补全图1；

②求证： $∠ C D B = ∠ M A C$ ；

(2)、连接 $B C$ ，写出一个 $B C$ 的值，使得对于任意一点C ，总有 $A B + B D = 3$ ，并证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，点A的坐标为 $(x_{1} ， y_{1})$ ，点B的坐标为 $(x_{2} ， y_{2})$ ，且 $x_{1} \neq x_{2}$ ， $y_{1} = y_{2}$ ．给出如下定义：若平面上存在一点P ，使 $△ A P B$ 是以线段 $A B$ 为斜边的直角三角形，则称点P为点A、点B的“直角点”．

(1)、已知点A的坐标为 $(1 ， 0)$ ．
①若点B的坐标为 $(5 ， 0)$ ，在点 $P_{1} (4 ， 3)$ 、 $P_{2} (3 ， - 2)$ 和 $P_{3} (2 ， \sqrt{3})$ 中，是点A、点B的“直角点”的是；

②点B在x轴的正半轴上，且 $A B = 2 \sqrt{2}$ ，当直线 $y = - x + b$ 上存在点A、点B的“直角点”时，求b的取值范围；

(2)、 $⊙ O$ 的半径为r ，点 $D (1 ， 4)$ 为点 $E (0 ， 2)$ 、点 $F (m ， n)$ 的“直角点”，若使得 $△ D E F$ 与 $⊙ O$ 有交点，直接写出半径r的取值范围．

查看试题解析