北京市海淀区2020年中考数学二模试卷
试卷更新日期:2020-07-09 类型:中考模拟
一、单选题
-
1. 下面的四个图形中,是圆柱的侧面展开图的是( )A、
 B、
B、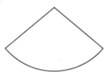 C、
C、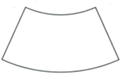 D、
D、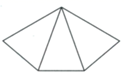 2. 若代数式 有意义,则实数x的取值范围是( )A、 B、 C、 D、3. 如图,在 中, ,通过测量,并计算 的面积,所得面积与下列数值最接近的是( )
2. 若代数式 有意义,则实数x的取值范围是( )A、 B、 C、 D、3. 如图,在 中, ,通过测量,并计算 的面积,所得面积与下列数值最接近的是( )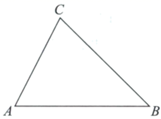 A、 B、 C、 D、4. 图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在( )
A、 B、 C、 D、4. 图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在( )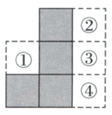 A、区域①处 B、区域②处 C、区域③处 D、区域④处5. 如图,在 中, , 平分 ,且 ,则 的度数为( )
A、区域①处 B、区域②处 C、区域③处 D、区域④处5. 如图,在 中, , 平分 ,且 ,则 的度数为( ) A、70° B、60° C、50° D、40°6. 如果 ,那么代数式 的值为( )A、1 B、2 C、3 D、47. 如图, 的半径等于4,如果弦 所对的圆心角等于90°,那么圆心O到弦 的距离为( )
A、70° B、60° C、50° D、40°6. 如果 ,那么代数式 的值为( )A、1 B、2 C、3 D、47. 如图, 的半径等于4,如果弦 所对的圆心角等于90°,那么圆心O到弦 的距离为( ) A、 B、2 C、 D、8. 在平面直角坐标系 中,对于点 ,若 ,则称点P为“同号点”.下列函数的图象中不存在“同号点”的是( )A、 B、 C、 D、
A、 B、2 C、 D、8. 在平面直角坐标系 中,对于点 ,若 ,则称点P为“同号点”.下列函数的图象中不存在“同号点”的是( )A、 B、 C、 D、二、填空题
-
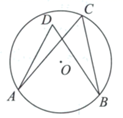
9. 单项式 的系数是.10. 如图,点A , B , C在 上,点D在 内,则 .(填“>”,“=”或“<”)
 11. 下表记录了一名篮球运动员在罚球线上投篮的结果:
11. 下表记录了一名篮球运动员在罚球线上投篮的结果:投篮次数n
48
82
124
176
230
287
328
投中次数m
33
59
83
118
159
195
223
投中频率
0.69
0.72
0.67
0.67
0.69
0.68
0.68
根据上表,这名篮球运动员投篮一次,投中的概率约为 . (结果精确到0.01)
12. 函数 的图象上有两点 ,若 ,写出一个正确的k的值: .13. 如图,在 中, ,过点B作 ,交 于点D , 若 ,则 的长度为 . 14. 如图,在平面直角坐标系 中,已知点 ,将 关于直线 对称,得到 ,则点C的对应点 的坐标为;再将 向上平移一个单位长度,得到 ,则点 的对应点 的坐标为 .
14. 如图,在平面直角坐标系 中,已知点 ,将 关于直线 对称,得到 ,则点C的对应点 的坐标为;再将 向上平移一个单位长度,得到 ,则点 的对应点 的坐标为 .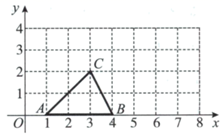 15. 小华和小明周末到北京三山五园绿道骑行.他们按设计好的同一条线路同时出发,小华每小时骑行 ,小明每小时骑行 ,他们完成全部行程所用的时间,小明比小华多半小时.设他们这次骑行线路长为 ,依题意,可列方程为 .16. 如图,在平面直角坐标系 中,有五个点 ,将二次函数 的图象记为W . 下列的判断中
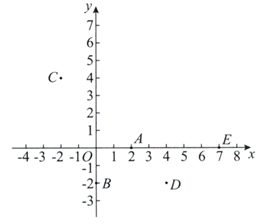
15. 小华和小明周末到北京三山五园绿道骑行.他们按设计好的同一条线路同时出发,小华每小时骑行 ,小明每小时骑行 ,他们完成全部行程所用的时间,小明比小华多半小时.设他们这次骑行线路长为 ,依题意,可列方程为 .16. 如图,在平面直角坐标系 中,有五个点 ,将二次函数 的图象记为W . 下列的判断中①点A一定不在W上;
②点B , C , D可以同时在W上;
③点C , E不可能同时在W上.
所有正确结论的序号是 .
三、解答题
-
17. 计算: .18. 解不等式 ,并在数轴上表示出它的解集.
 19. 下面是小王同学“过直线外一点作该直线的平行线”的尺规作图过程.
19. 下面是小王同学“过直线外一点作该直线的平行线”的尺规作图过程.已知:直线l及直线l外一点P .
求作:直线 ,使得 .

作法:如图,
①在直线l外取一点A , 作射线 与直线l交于点B ,
②以A为圆心, 为半径画弧与直线l交于点C , 连接 ,
③以A为圆心, 为半径画弧与线段 交于点 ,
则直线 即为所求.
根据小王设计的尺规作图过程,
 (1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明:∵ ,
∴ ,( ▲ )(填推理的依据).
∵ ▲ ,
∴ .
∵ ,
∴ .
∴ ( ▲ )(填推理的依据).
即 .
20. 已知关于x的一元二次方程 .(1)、如果此方程有两个相等的实数根,求n的值;(2)、如果此方程有一个实数根为0,求另外一个实数根.21. 如图,在 中, ,D为 的中点,连接 ,过点A作 ,过点C作 与 相交于点G .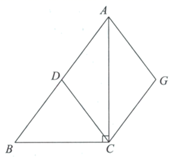 (1)、求证:四边形 是菱形(2)、若 ,求 的长.22. 坚持节约资源和保护环境是我国的基本国策,国家要求加强生活垃圾分类回收与再生资源回收有效衔接,提高全社会资源产出率,构建全社会的资源循环利用体系.
(1)、求证:四边形 是菱形(2)、若 ,求 的长.22. 坚持节约资源和保护环境是我国的基本国策,国家要求加强生活垃圾分类回收与再生资源回收有效衔接,提高全社会资源产出率,构建全社会的资源循环利用体系.图1反映了2014—2019年我国生活垃圾清运量的情况.
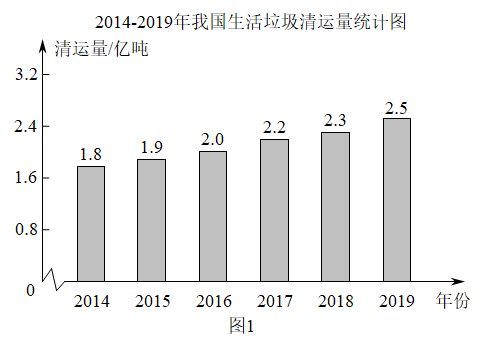
图2反映了2019年我国G市生活垃圾分类的情况.
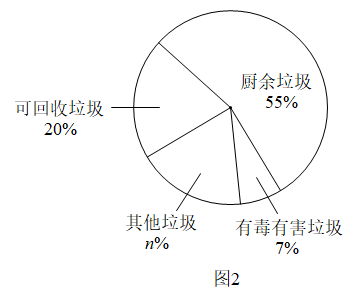
根据以上材料回答下列问题:
(1)、图2中,n的值为;(2)、2014—2019年,我国生活垃圾清运量的中位数是;(3)、据统计,2019年G市清运的生活垃圾中可回收垃圾约为0.02亿吨,所创造的经济总价值约为40亿元.若2019年我国生活垃圾清运量中,可回收垃圾的占比与G市的占比相同,根据G市的数据估计2019年我国可回收垃圾所创造的经济总价值是多少.23. 如图, 为 的直径,C为 上一点, 于点E , 的切线 交 的延长线于点D . (1)、求证: ;(2)、若 .求 的长.24. 如图,在平面直角坐标系 中,函数 的图象与直线 交于点 .M是函数 图象上一点,过M作x轴的平行线交直线 于点N .
(1)、求证: ;(2)、若 .求 的长.24. 如图,在平面直角坐标系 中,函数 的图象与直线 交于点 .M是函数 图象上一点,过M作x轴的平行线交直线 于点N . (1)、求k和p的值;(2)、设点M的横坐标为m .
(1)、求k和p的值;(2)、设点M的横坐标为m .①求点N的坐标;(用含m的代数式表示)
②若 的面积大于 ,结合图象直接写出m的取值范围.
25. 如图1,在四边形 中,对角线 平分 .为了研究图中线段之间的数量关系,设 .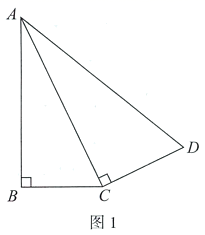 (1)、由题意可得 ,(在括号内填入图1中相应的线段)y关于x的函数表达式为 ;(2)、如图2,在平面直角坐标系 中,根据(1)中y关于x的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;
(1)、由题意可得 ,(在括号内填入图1中相应的线段)y关于x的函数表达式为 ;(2)、如图2,在平面直角坐标系 中,根据(1)中y关于x的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;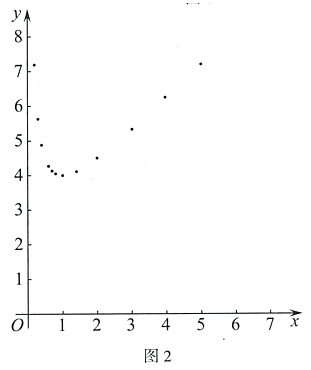 (3)、①当 时,y随x的增大而增大(答(3)结合函数图象,解决问题:
(3)、①当 时,y随x的增大而增大(答(3)结合函数图象,解决问题:①写出该函数的一条性质:;
②估计 的最小值为 . (结果精确到0.1)
26. 在平面直角坐标系 中,已知二次函数 的图象与x轴交于点 ,与y轴交于点B , 将其图象在点A , B之间的部分(含A , B两点)记为F .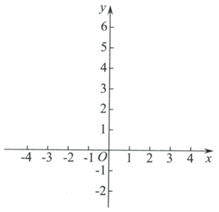 (1)、求点B的坐标及该函数的表达式;(2)、若二次函数 的图象与F只有一个公共点,结合函数图象,求a的取值范围.27. 如图1,等边三角形 中,D为 边上一点,满足 ,连接 ,以点A为中心,将射线 顺时针旋转60°,与 的外角平分线 交于点E .
(1)、求点B的坐标及该函数的表达式;(2)、若二次函数 的图象与F只有一个公共点,结合函数图象,求a的取值范围.27. 如图1,等边三角形 中,D为 边上一点,满足 ,连接 ,以点A为中心,将射线 顺时针旋转60°,与 的外角平分线 交于点E .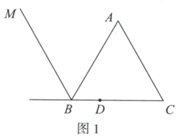
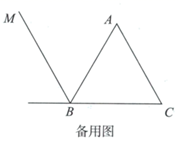 (1)、依题意补全图1;(2)、求证: ;(3)、若点B关于直线 的对称点为F , 连接 .求证: ;(4)、若点B关于直线 的对称点为F , 连接 若 成立,直接写出 的度数为°.28. 在平面内,对于给定的 ,如果存在一个半圆或优弧与 的两边相切,且该弧上的所有点都在 的内部或边上,则称这样的弧为 的内切弧.当内切弧的半径最大时,称该内切弧为 的完美内切弧.(注:弧的半径指该弧所在圆的半径)
(1)、依题意补全图1;(2)、求证: ;(3)、若点B关于直线 的对称点为F , 连接 .求证: ;(4)、若点B关于直线 的对称点为F , 连接 若 成立,直接写出 的度数为°.28. 在平面内,对于给定的 ,如果存在一个半圆或优弧与 的两边相切,且该弧上的所有点都在 的内部或边上,则称这样的弧为 的内切弧.当内切弧的半径最大时,称该内切弧为 的完美内切弧.(注:弧的半径指该弧所在圆的半径)在平面直角坐标系 中, .
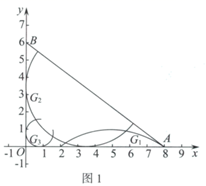
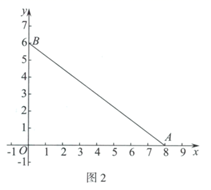
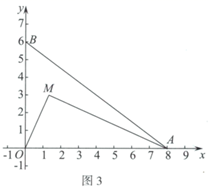
 (1)、如图1,在弧 ,弧 ,弧 中,是 的内切弧的是;(2)、如图2,若弧G为 的内切弧,且弧G与边 相切,求弧G的半径的最大值;(3)、如图3,动点 ,连接 .
(1)、如图1,在弧 ,弧 ,弧 中,是 的内切弧的是;(2)、如图2,若弧G为 的内切弧,且弧G与边 相切,求弧G的半径的最大值;(3)、如图3,动点 ,连接 .①直接写出 的完美内切弧的半径的最大值;
②记①中得到的半径最大时的完美内切弧为弧T . 点P为弧T上的一个动点,过点P作x轴的垂线,分别交x轴和直线 于点D , E , 点F为线段 的中点,直接写出线段 长度的取值范围.