北京市东城区2020年中考数学二模试卷
试卷更新日期:2020-07-09 类型:中考模拟
一、单选题
-
1. 在实数 ,-3, , 中,最小的数是( )A、 B、-3 C、|-3.14| D、2. 如图,在平面直角坐标系中,已知点 ,点 ,平移线段AB,使点A落在点 处,则点B的对应点 的坐标为( )
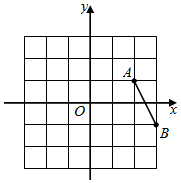 A、 B、 C、 D、3. 判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )A、﹣2 B、﹣ C、0 D、4. 若点 在抛物线 上,则下列结论正确的是( )A、 B、 C、 D、5. 如图,小明从A处出发沿北偏东 方向行走至B处,又从B处沿南偏东 方向行走至C处,则 等于( )
A、 B、 C、 D、3. 判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )A、﹣2 B、﹣ C、0 D、4. 若点 在抛物线 上,则下列结论正确的是( )A、 B、 C、 D、5. 如图,小明从A处出发沿北偏东 方向行走至B处,又从B处沿南偏东 方向行走至C处,则 等于( ) A、 B、 C、 D、6. 把边长分别为1和2的两个正方形按图 的方式放置.则图中阴影部分的面积为( )
A、 B、 C、 D、6. 把边长分别为1和2的两个正方形按图 的方式放置.则图中阴影部分的面积为( ) A、 B、 C、 D、7. 如图,已知正五边形 ABCDE内接于⊙O,连结BD,则∠ABD的度数是( )
A、 B、 C、 D、7. 如图,已知正五边形 ABCDE内接于⊙O,连结BD,则∠ABD的度数是( ) A、60° B、70° C、72° D、144°8. 五名学生投篮球,每人投10次,统计他们每人投中的次数.得到五个数据,并对数据进行整理和分析给出如下信息:
A、60° B、70° C、72° D、144°8. 五名学生投篮球,每人投10次,统计他们每人投中的次数.得到五个数据,并对数据进行整理和分析给出如下信息:平均数
中位数
众数
m
6
7
则下列选项正确的是( )
A、可能会有学生投中了8次 B、五个数据之和的最大值可能为30 C、五个数据之和的最小值可能为20 D、平均数m一定满足二、填空题
-
9. 分解因式: .10. 在“中国汉字听写大赛”选拔赛中,甲、乙两位同学的平均分都是90分,甲同学成绩的方差是15,乙同学成绩的方差是3,由此推断甲、乙两人中成绩稳定的是 .11. 若点 在直线 上,则a的值等于 .12. 在平面直角坐标系中, 三个顶点的坐标分别为 .以原点 为位似中心,把这个三角形缩小为原来的 ,得到 ,则点 的对应点 的坐标是 .13. 已知圆锥的母线长为5cm,侧面积为15π ,则这个圆锥的底面圆半径为cm.14. 如图,在 中,AB的垂直平分线交A于点D , 交BC于点E , 若 , ,则 的周长为 .
 15. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,则 的值为 .
15. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,则 的值为 .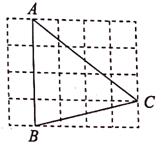 16. 某快餐店外卖促销,佳佳和点点想点外卖,每单需支付送餐费5元,每种餐食外卖价格如下表:
16. 某快餐店外卖促销,佳佳和点点想点外卖,每单需支付送餐费5元,每种餐食外卖价格如下表:餐食种类
价格(单位:元)
汉堡套餐
40
鸡翅
16
鸡块
15
冰激凌
14
蔬菜沙拉
9
促销活动:
①汉堡套餐5折优惠,每单仅限一套;
②全部商品(包括打折套餐)满20元减4元,满40元减10元,满60元减15元,满80元减20元.
佳佳想要汉堡套餐、鸡翅、冰激凌、蔬菜沙拉各一份;点点想要汉堡套餐、鸡块、冰激凌各一份,若他们把想要的都买全,最少要花元(含送餐费).
三、解答题
-
17. 下面是“作一个 角”的尺规作图过程.
已知:平面内一点A .
求作: ,使得 .
作法:如图,

①作射线 ;
②在射线 取一点O , 以O为圆心, 长为半径作圆,与射线 相交于点C;
③分别以 为圆心,大于 为半径作弧,两弧交于点D , 作射线 交 于点E;
④作射线 .
则 即为所求作的角.
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明: ,
.
.()(填推理的依据)
18. 解不等式 ,并把它的解集在数轴上表示出来. 19. 已知 ,求代数式 的值.20. 如图,在 中,以点B为圆心, 长为半径画弧,交 边于点D , 连接 .若 , ,求 的度数.
19. 已知 ,求代数式 的值.20. 如图,在 中,以点B为圆心, 长为半径画弧,交 边于点D , 连接 .若 , ,求 的度数.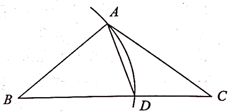 21. 在菱形 中,对角线 相交于点O , E为 的中点,连接 并延长到点F , 使 ,连接 .
21. 在菱形 中,对角线 相交于点O , E为 的中点,连接 并延长到点F , 使 ,连接 .
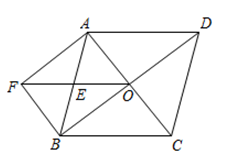 (1)、求证:四边形 是矩形;(2)、若 ,求 的长.22. 在平面直角坐标系 中,反比例函数 的图象经过点 ,直线 与x轴交于点 .(1)、求 的值;(2)、已知点 ,过点P作平行于x轴的直线,交直线 于点C , 过点P作平行于y轴的直线交反比例函数 的图象于点D , 当 时,结合函数的图象,求出n的值.23. 教育未来指数是为了评估教育系统在培养学生如何应对快速多变的未来社会方面所呈现的效果.现对教育未来指数得分前35名的国家和地区的有关数据进行收集、整理、描述和分析后,给出了部分信息.
(1)、求证:四边形 是矩形;(2)、若 ,求 的长.22. 在平面直角坐标系 中,反比例函数 的图象经过点 ,直线 与x轴交于点 .(1)、求 的值;(2)、已知点 ,过点P作平行于x轴的直线,交直线 于点C , 过点P作平行于y轴的直线交反比例函数 的图象于点D , 当 时,结合函数的图象,求出n的值.23. 教育未来指数是为了评估教育系统在培养学生如何应对快速多变的未来社会方面所呈现的效果.现对教育未来指数得分前35名的国家和地区的有关数据进行收集、整理、描述和分析后,给出了部分信息.a.教育未来指数得分的频数分布直方图(数据分成7组: , , , , , , );

b.教育未来指数得分在 这一组的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
c.35个国家和地区的人均国内生产总值和教育未来指数得分情况统计图如下:

d.中国和中国香港的教育未来指数得分分别为32.9和68.5.
(以上数据来源于《国际统计年鉴(2018)》和国际在线网)
根据以上信息,回答下列问题:
(1)、中国香港的教育未来指数得分排名世界第;(2)、在35个国家和地区的人均国内生产总值和教育未来指数得分情况统计图中,包括中国香港在内的少数几个国家和地区所对应的点位于虚线l的上方,请在图中用“○”画出代表中国香港的点;(3)、在教育未来指数得分比中国高的国家和地区中,人均国内生产总值的最大值约为万美元;(结果保留一位小数)(4)、下列推断合理的是 . (只填序号即可)①相较于点 所代表的国家和地区,中国的教育未来指数得分还有一定差距,“十三五”规划提出“教育优先发展,教育强则国家强”的任务,进一步提高国家教育水平;
②相较于点 所代表的国家和地区,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
24. 如图,在 中, ,P是 上的动点,D是 延长线上的定点,连接 交 于点Q .
小明根据学习函数的经验,对线段 的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)、对于点P在 上的不同位置,画图测量,得到了线段 的长度(单位:cm)的几组值,如下表:位置1
位置2
位置3
位置4
位置5
位置6
位置7
0.00
1.00
2.00
3.00
4.00
5.00
6.00
4.99
4.56
4.33
4.23
4.53
4.95
5.51
4.99
3.95
3.31
2.95
2.80
2.79
2.86
在 的长度这三个量中,确定的长度是自变量,的长度和的长度都是这个自变量的函数;
(2)、在同一平面直角坐标系 中,画出(1)中所确定的函数的图象; (3)、结合函数图象,解决问题:当 时, 的长度约为cm.25. 如图, 内接于 , 为直径,作 交 于点 ,延长 , 交于点 ,过点 作 的切线 ,交 于点
(3)、结合函数图象,解决问题:当 时, 的长度约为cm.25. 如图, 内接于 , 为直径,作 交 于点 ,延长 , 交于点 ,过点 作 的切线 ,交 于点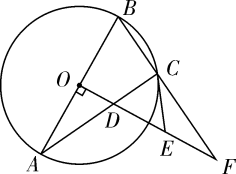 (1)、求证: ;(2)、如果 , ,求弦 的长.26. 在平面直角坐标系 中,点A的坐标为 ,点B的坐标为 ,抛物线 的顶点为C .(1)、若抛物线经过点B时,求顶点C的坐标;(2)、若抛物线与线段 恰有一个公共点,结合函数图象,求a的取值范围;(3)、若满足不等式 的x的最大值为3,直接写出实数a的值.27. 在 中, ,点D是 外一点,点D与点C在直线 的异侧,且点 不共线,连接 .
(1)、求证: ;(2)、如果 , ,求弦 的长.26. 在平面直角坐标系 中,点A的坐标为 ,点B的坐标为 ,抛物线 的顶点为C .(1)、若抛物线经过点B时,求顶点C的坐标;(2)、若抛物线与线段 恰有一个公共点,结合函数图象,求a的取值范围;(3)、若满足不等式 的x的最大值为3,直接写出实数a的值.27. 在 中, ,点D是 外一点,点D与点C在直线 的异侧,且点 不共线,连接 .
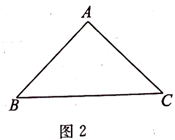 (1)、如图1,当 时,画出图形,直接写出 之间的数量关系;(2)、当 时,利用图2,继续探究 之间的数量关系并证明;
(1)、如图1,当 时,画出图形,直接写出 之间的数量关系;(2)、当 时,利用图2,继续探究 之间的数量关系并证明;(提示:尝试运用图形变换,将要研究的有关线段尽可能转移到一个三角形中)
(3)、当 时,进一步探究 之间的数量关系,并用含 的等式直接表示出它们之间的关系.28. 对于平面直角坐标系 内任意一点P , 过P点作 轴于点M , 轴于点N , 连接 ,则称 的长度为点P的垂点距离,记为h . 特别地,点P与原点重合时,垂点距离为0. (1)、点 的垂点距离分别为 , , ;(2)、点P在以 为圆心,半径为3的 上运动,求出点P的垂点距离h的取值范围;(3)、点T为直线 位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
(1)、点 的垂点距离分别为 , , ;(2)、点P在以 为圆心,半径为3的 上运动,求出点P的垂点距离h的取值范围;(3)、点T为直线 位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.