安徽省芜湖市无为县2020年中考数学一模试卷
试卷更新日期:2020-07-09 类型:中考模拟
一、单选题
-
1. 点(﹣3,﹣4)关于坐标原点对称的点的坐标是( )A、(3,4) B、(﹣4,﹣3) C、(﹣3,4) D、(3,﹣4)2. 若抛物线y=﹣2x2+3x﹣1可由抛物线y=ax2通过平移得到,则a的值是( )A、3 B、0 C、﹣1 D、﹣23. 如图,是5个大小相同的小正方体的组合体,则它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,在6×6网格中,∠α的顶点在格点上(网格线的交点),两边分别经过格点,则tanα的值是( )
4. 如图,在6×6网格中,∠α的顶点在格点上(网格线的交点),两边分别经过格点,则tanα的值是( ) A、2 B、 C、 D、5. 某校生物兴趣小组为了解种子发芽情况,重复做了大量种子发芽的实验,结果如下:
A、2 B、 C、 D、5. 某校生物兴趣小组为了解种子发芽情况,重复做了大量种子发芽的实验,结果如下: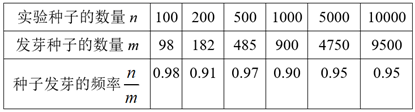
根据以上数据,估计该种子发芽的概率是( )
A、0.90 B、0.98 C、0.95 D、0.916. 如图,直线y=ax+b(a≠0)与双曲线y= (k≠0)交于点A(﹣2,3)和点B(m , ﹣1),则不等式ax+b< 的解集是( ) A、x ﹣2 B、x 6 C、x ﹣2或0 x 6 D、﹣2 x 0或x 67. 下列说法正确的是( )A、经过有交通信号灯的路口,遇到绿灯是必然事件 B、抛掷一枚均匀的硬币,10次都是正面朝上是随机事件 C、“明天下雨的概率是40%”就是说“明天有40%的时间都在下雨” D、从装有3个红球和4个黑球的袋子里摸出一个球是红球的概率是8. 如图,在平行四边形ABCD中,AD=BD=5,AB=6,E为AB的中点,F为CD上一点,连接EF交BD于点G , 若S△FDG:S△EDG=2:3,则EF的长是( )
A、x ﹣2 B、x 6 C、x ﹣2或0 x 6 D、﹣2 x 0或x 67. 下列说法正确的是( )A、经过有交通信号灯的路口,遇到绿灯是必然事件 B、抛掷一枚均匀的硬币,10次都是正面朝上是随机事件 C、“明天下雨的概率是40%”就是说“明天有40%的时间都在下雨” D、从装有3个红球和4个黑球的袋子里摸出一个球是红球的概率是8. 如图,在平行四边形ABCD中,AD=BD=5,AB=6,E为AB的中点,F为CD上一点,连接EF交BD于点G , 若S△FDG:S△EDG=2:3,则EF的长是( ) A、 B、2 C、2 D、59. 如图,正方形ABCD边长为4,E、F、G、H分别是AB、BC、CD、DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能是( )
A、 B、2 C、2 D、59. 如图,正方形ABCD边长为4,E、F、G、H分别是AB、BC、CD、DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能是( )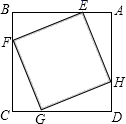 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在等边△ABC中,AB=12,点D在AB边上,AD=4,E为AC中点,P为△ABC内一点,且∠BPD=90°,则线段PE的最小值为( )
10. 如图,在等边△ABC中,AB=12,点D在AB边上,AD=4,E为AC中点,P为△ABC内一点,且∠BPD=90°,则线段PE的最小值为( ) A、3 ﹣2 B、 C、2 ﹣4 D、4 ﹣8
A、3 ﹣2 B、 C、2 ﹣4 D、4 ﹣8二、填空题
-
11. 线段AB长为10cm , 点C是AB的黄金分割点,则AC的长为(结果精确到0.1cm).12. 某工厂今年一月份生产防疫护目镜的产量是20万件,计划之后两个月增加产量,如果月平均增长率为x , 那么第一季度防疫护目镜的产量y(万件)与x之间的关系应表示为 .13. 如图,直线y=ax+b(a≠0)与x轴交于点B , 与y轴交于点A , 与双曲线y= (k≠0)交于点C , 若AB=BC , △AOC的面积为4,则k的值是 .
 14. 如图,Rt△ABC中,∠C=90°,AC=8,BC=16,点D在边BC上,点E在边AB上,沿DE将△ABC折叠,使点B与点A重合,连接AD , 点P是线段AD上一动点,当半径为5的⊙P与△ABC的一边相切时,AP的长为 .
14. 如图,Rt△ABC中,∠C=90°,AC=8,BC=16,点D在边BC上,点E在边AB上,沿DE将△ABC折叠,使点B与点A重合,连接AD , 点P是线段AD上一动点,当半径为5的⊙P与△ABC的一边相切时,AP的长为 . 15. 如图
15. 如图 (1)、如图,矩形ABCD的对角线长为a , 对角线与一边的夹角为α(α≤45°),则CD=(用α的三角函数和a来表示),S△BCD=(用α的三角函数和a来表示)=(用2α的三角函数和a来表示);(2)、猜想并直接写出sin2α,sinα,cosα之间的数量关系.
(1)、如图,矩形ABCD的对角线长为a , 对角线与一边的夹角为α(α≤45°),则CD=(用α的三角函数和a来表示),S△BCD=(用α的三角函数和a来表示)=(用2α的三角函数和a来表示);(2)、猜想并直接写出sin2α,sinα,cosα之间的数量关系.三、解答题
-
16. 用配方法解方程:17. 小明同学在数学实践活动课中测景路灯的高度,如图,已知她的目高AB为1.5米,街为站在A处看路灯顶端P的仰角为30°.再往前走2米站在C处,看路灯顶端P的仰角为45°,求路灯顶端P到地面的距离(结果保留根号).
 18. 如图,由边长为1个单位长度的小正方形组成的网格中,已知格点△ABC(顶点是网格线的交点)和格点O .
18. 如图,由边长为1个单位长度的小正方形组成的网格中,已知格点△ABC(顶点是网格线的交点)和格点O . (1)、画出△ABC绕点O逆时针方向旋转90°得到的△A1B1C1;(2)、画出△A1B1C1向下平移4个单位长度得到的△A2B2C2 .19. 如图是一个几何体的三视图(单位:cm).
(1)、画出△ABC绕点O逆时针方向旋转90°得到的△A1B1C1;(2)、画出△A1B1C1向下平移4个单位长度得到的△A2B2C2 .19. 如图是一个几何体的三视图(单位:cm). (1)、这个几何体的名称是;(2)、根据图中尺寸,求这个几何体的表面积.(结果保留π)20. 如图,点C是⊙O的直径AB延长线上一点,过⊙O上一点D作DF⊥AB于F , 交⊙O于点E , 点M是BE的中点,AB=4,∠E=∠C=30°.
(1)、这个几何体的名称是;(2)、根据图中尺寸,求这个几何体的表面积.(结果保留π)20. 如图,点C是⊙O的直径AB延长线上一点,过⊙O上一点D作DF⊥AB于F , 交⊙O于点E , 点M是BE的中点,AB=4,∠E=∠C=30°. (1)、求证:CD是⊙O的切线;(2)、求DM的长.21. 在一个不透明的盒子中装有6张卡片,6张卡片的正面分别标有数字﹣4,﹣3,﹣2,﹣1,6,8,这些卡片除数字外都相同,将卡片搅匀.(1)、从盒子中任意抽取一张卡片,求恰好抽到标有偶数卡片的概率;(2)、先从盒子中任意抽取一张卡片,把它上面的数字作为一个点的横坐标,不放回,再从盒子剩余的卡片中任意抽取一张卡片,把它上面的数字作为这个点的纵坐标,求抽取的点恰好落在第二象限的概率.22. 某商场经销一种成本价为20元/件的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于成本价的1.8倍,在试销售过程中发现每天的销量y(件)与售价x(元/件)之间满足一次函数关系,对应关系如下表所示:
(1)、求证:CD是⊙O的切线;(2)、求DM的长.21. 在一个不透明的盒子中装有6张卡片,6张卡片的正面分别标有数字﹣4,﹣3,﹣2,﹣1,6,8,这些卡片除数字外都相同,将卡片搅匀.(1)、从盒子中任意抽取一张卡片,求恰好抽到标有偶数卡片的概率;(2)、先从盒子中任意抽取一张卡片,把它上面的数字作为一个点的横坐标,不放回,再从盒子剩余的卡片中任意抽取一张卡片,把它上面的数字作为这个点的纵坐标,求抽取的点恰好落在第二象限的概率.22. 某商场经销一种成本价为20元/件的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于成本价的1.8倍,在试销售过程中发现每天的销量y(件)与售价x(元/件)之间满足一次函数关系,对应关系如下表所示: (1)、求y与x之间的函数表达式,并写出自变量x的取值范围;(2)、该商场销售这种商品每天所获得的利润为w元,若每天销售这种商品需支付人员工资、管理费等各项费用共200元,求w与x之间的函数表达式;并求出这种商品销售单价定为多少时,才能使商场每天获取的利润最大?最大利润是多少?23. 如图,在△ABC中,AB=AC , AD是边BC上的中线,BE⊥AC于点E , 交AD于点H过点C作CF∥AB交BE的延长线于点F .
(1)、求y与x之间的函数表达式,并写出自变量x的取值范围;(2)、该商场销售这种商品每天所获得的利润为w元,若每天销售这种商品需支付人员工资、管理费等各项费用共200元,求w与x之间的函数表达式;并求出这种商品销售单价定为多少时,才能使商场每天获取的利润最大?最大利润是多少?23. 如图,在△ABC中,AB=AC , AD是边BC上的中线,BE⊥AC于点E , 交AD于点H过点C作CF∥AB交BE的延长线于点F .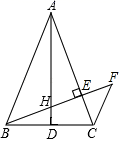 (1)、求证:△ABH∽△BFC;(2)、求证:BH2=HE•HF;(3)、若AB=2,∠BAC=45°,求BH的长.
(1)、求证:△ABH∽△BFC;(2)、求证:BH2=HE•HF;(3)、若AB=2,∠BAC=45°,求BH的长.