安徽省合肥五十中天鹅湖教育集团2020年中考数学一模试卷
试卷更新日期:2020-07-09 类型:中考模拟
一、单选题
-
1. 四个有理数﹣2,5,0,﹣4,其中最小的是( )A、﹣2 B、5 C、0 D、﹣42. 以下运算正确的是( )A、 B、 C、 D、3. 由4个完全相同的小正方体组成的立体图形如图所示,则该立体图形的俯视图是( )
 A、
A、 B、
B、 C、
C、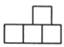 D、
D、 4. 纳米(nm)是种非常小的长度单位,1nm= m,如果某冠状病毒的直径为110nm,那么用科学记数法表示该冠状病毒的直径为( )A、 B、 C、 D、5. 如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=48°,则∠2的度数是( )
4. 纳米(nm)是种非常小的长度单位,1nm= m,如果某冠状病毒的直径为110nm,那么用科学记数法表示该冠状病毒的直径为( )A、 B、 C、 D、5. 如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=48°,则∠2的度数是( ) A、64° B、65 ° C、66° D、67°6. 为执行“均衡教育“政策,某区2017年投入教育经费2500万元,预计到2019年底三年累计投入1.2亿元,若每年投入教育经费的年平均增长百分率为x,则下列方程正确的是( )A、2500(1+2x)=12000 B、2500+2500(1+x)+2500(1+2x)=12000 C、2500(1+x)2=1200 D、2500+2500(1+x)+2500(1+x)2=120007. 如表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
A、64° B、65 ° C、66° D、67°6. 为执行“均衡教育“政策,某区2017年投入教育经费2500万元,预计到2019年底三年累计投入1.2亿元,若每年投入教育经费的年平均增长百分率为x,则下列方程正确的是( )A、2500(1+2x)=12000 B、2500+2500(1+x)+2500(1+2x)=12000 C、2500(1+x)2=1200 D、2500+2500(1+x)+2500(1+x)2=120007. 如表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)成绩(个/分钟)
140
160
169
170
177
180
人数
1
1
1
2
3
2
则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
A、众数是177 B、平均数是170 C、中位数是173.5 D、方差是1358. 关于x的一元二次方程 ,下列结论一定正确的是( )A、该方程没有实数根 B、该方程有两个不相等的实数根 C、该方程有两个相等的实数根 D、无法确定9. 甲、乙两人在一条长为600m的笔直道路上均匀地跑步,速度分别为 和 ,起跑前乙在起点,甲在乙前面50m处,若两人同时起跑,则从起跑出发到其中一人先到达终点的过程中,两人之间的距离y(m)与时间t(s)的函数图象是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在边长为 的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF= 的点P的个数是( )
10. 如图,在边长为 的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF= 的点P的个数是( ) A、0 B、4 C、8 D、16
A、0 B、4 C、8 D、16二、填空题
-
11. 因式分解: .12. 不等式组 的解集是.13. 如图,在 中, , , ,以点A为圆心,以AC为半径画弧,交AB于D,则扇形CAD的周长是(结果保留 ).
 14. 对于实数a,b,定义新运算“ ”:a b= ;若关于x的方程 恰好有两个不相等的实根,则t的值为 .
14. 对于实数a,b,定义新运算“ ”:a b= ;若关于x的方程 恰好有两个不相等的实根,则t的值为 .三、解答题
-
15. 计算: .16. 如图所示,在边长为1个单位长度的小正方形组成的网格中, 的顶点A,B,C在格点(网格线的交点)上.
 (1)、将 绕点B逆时针旋转 ,得到 ,画出 ;(2)、以点A为位似中心放大 ,得到 ,使 与 的位似比为2:1,请你在网格内画出 .17. 我国古代《算法统宗》里有这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每间客房住7人,那么有7人无房可住;如果每间客房住9人,那么就空出一间房.求该店有客房多少间?房客多少人?18. 如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
(1)、将 绕点B逆时针旋转 ,得到 ,画出 ;(2)、以点A为位似中心放大 ,得到 ,使 与 的位似比为2:1,请你在网格内画出 .17. 我国古代《算法统宗》里有这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每间客房住7人,那么有7人无房可住;如果每间客房住9人,那么就空出一间房.求该店有客房多少间?房客多少人?18. 如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠): (1)、填写下表:
(1)、填写下表:正方形ABCD内点的个数
1
2
3
4
. ..
n
分割成三角形的个数
4
6
. .
(2)、原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.19. 很多交通事故是由于超速行驶导致的,为集中治理超速现象,高速交警在距离高速路40米的地方设置了一个测速观察点,现测得测速点的西北方向有一辆小型轿车从B处沿西向正东方向行驶,2秒钟后到达测速点北偏东 的方向上的C处,如图.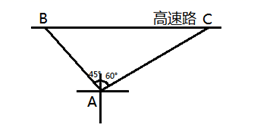 (1)、求该小型轿车在测速过程中的平均行驶速度约是多少千米/时(精确到1千米/时)?
(1)、求该小型轿车在测速过程中的平均行驶速度约是多少千米/时(精确到1千米/时)?(参考数据: )
(2)、我国交通法规定:小轿车在高速路行驶,时速超过限定速度10%以上不到50%的处200元罚款,扣3分;时速超过限定速度50%以上不到70%的处1500元罚款,扣12分;时速超过限定时速70%以上的处1500元罚款,扣12分.若该高速路段限速120千米/时,你认为该小轿车驾驶员会受到怎样的处罚.20. 如图,反比例函数 和一次函数 相交于点 , .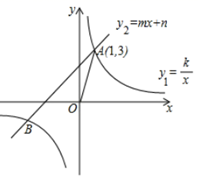 (1)、求一次函数和反比例函数解析式;(2)、连接OA,试问在x轴上是否存在点P,使得 为以OA为腰的等腰三角形,若存在,直接写出满足题意的点P的坐标;若不存在,说明理由.21. 张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
(1)、求一次函数和反比例函数解析式;(2)、连接OA,试问在x轴上是否存在点P,使得 为以OA为腰的等腰三角形,若存在,直接写出满足题意的点P的坐标;若不存在,说明理由.21. 张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:组别
步数分组
频率
A
x<6000
0.1
B
6000≤x<7000
0.5
C
7000≤x<8000
m
D
x≥8000
n
合计
1

根据信息解答下列问题:
(1)、填空:m= , n=;并补全条形统计图;(2)、这20名朋友一天行走步数的中位数落在组;(填组别)(3)、张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.22. 某市政府为了扶贫,鼓励当地农民养殖小龙虾,如图:张叔叔顺着圩梗AN、AM(AN=3 m , AM=10m , ∠MAN=45°),用8m长的渔网搭建了一个养殖水域(即四边形ABCD),圩梗边不需要渔网,AB∥CD , ∠C=90°.设BC=xm , 四边形ABCD面积为S(m2). (1)、求出S关于x的函数表达式及x的取值范围;(2)、x为何值时,围成的养殖水域面积最大?最大面积是多少?23. 如图,在 中,AB<AC,点D、F分别为BC、AC的中点,E点在边AC上,连接DE,过点B作DE的垂线交AC于点G,垂足为点H,且 与四边形ABDE的周长相等,设AC=b,AB=c.
(1)、求出S关于x的函数表达式及x的取值范围;(2)、x为何值时,围成的养殖水域面积最大?最大面积是多少?23. 如图,在 中,AB<AC,点D、F分别为BC、AC的中点,E点在边AC上,连接DE,过点B作DE的垂线交AC于点G,垂足为点H,且 与四边形ABDE的周长相等,设AC=b,AB=c. (1)、求线段CE的长度;(2)、求证:DF=EF;(3)、若 ,求 的值.
(1)、求线段CE的长度;(2)、求证:DF=EF;(3)、若 ,求 的值.