安徽省合肥四十二中2020年中考数学一模试卷
试卷更新日期:2020-07-09 类型:中考模拟
一、单选题
-
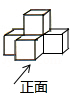
1. 一个由5个相同的小正方体组成的立体图形如图所示,则从正面看到的平面图形是( )
 A、
A、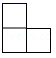 B、
B、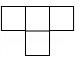 C、
C、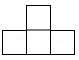 D、
D、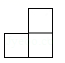 2. 若点A(x1 , ﹣3),B(x2 , 1),C(x3 , 2)在反比例函数y= 的图象上,则x1 , x2 , x3的大小关系是( )A、x1<x3<x2 B、x1<x2<x3 C、x2<x3<x1 D、x3<x2<x13. 在平面直角坐标系中,将抛物线y=x2﹣2x﹣1先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式是( )A、y=(x+1)2+1 B、y=(x﹣3)2+1 C、y=(x﹣3)2﹣5 D、y=(x+1)2+24. 如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm , OA′=20cm , 则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是( )
2. 若点A(x1 , ﹣3),B(x2 , 1),C(x3 , 2)在反比例函数y= 的图象上,则x1 , x2 , x3的大小关系是( )A、x1<x3<x2 B、x1<x2<x3 C、x2<x3<x1 D、x3<x2<x13. 在平面直角坐标系中,将抛物线y=x2﹣2x﹣1先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式是( )A、y=(x+1)2+1 B、y=(x﹣3)2+1 C、y=(x﹣3)2﹣5 D、y=(x+1)2+24. 如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm , OA′=20cm , 则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是( )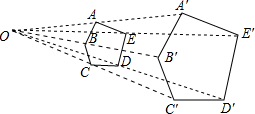 A、1:2 B、2:1 C、1:3 D、3:15. 已知抛物线 经过 和 两点,则n的值为( )A、﹣2 B、﹣4 C、2 D、46. 若函数 与 的图象如图所示,则函数 的大致图象为( )
A、1:2 B、2:1 C、1:3 D、3:15. 已知抛物线 经过 和 两点,则n的值为( )A、﹣2 B、﹣4 C、2 D、46. 若函数 与 的图象如图所示,则函数 的大致图象为( )
 A、
A、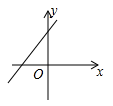 B、
B、 C、
C、 D、
D、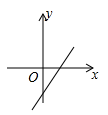 7. 某路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小明到达该路口时,遇到绿灯的概率是( )A、 B、 C、 D、8. 如图, 是等边三角形,被一矩形所截, 被截成三等分,EH∥BC,则四边形 的面积是 的面积的:( )
7. 某路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小明到达该路口时,遇到绿灯的概率是( )A、 B、 C、 D、8. 如图, 是等边三角形,被一矩形所截, 被截成三等分,EH∥BC,则四边形 的面积是 的面积的:( )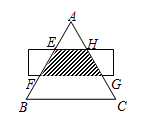 A、 B、 C、 D、9. 如图,从一块直径为 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为( )
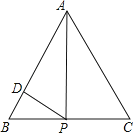
A、 B、 C、 D、9. 如图,从一块直径为 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为( )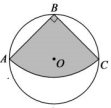 A、 B、 C、 D、10.
A、 B、 C、 D、10.如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
 A、
A、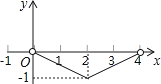 B、
B、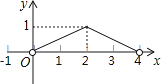 C、
C、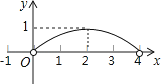 D、
D、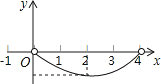
二、填空题
-
11. 已知 ,则 的值为.12. 在Rt△ABC中,∠C=90°,如果tan∠A= ,那么cosB= .13. 如图,圆锥的母线长为10cm,高为8cm,则该圆锥的侧面展开图(扇形)的弧长为cm.(结果用π表示)
 14. 如图,CD=4,∠C=90°,点B在线段CD上, ,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为 .
14. 如图,CD=4,∠C=90°,点B在线段CD上, ,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为 .
三、解答题
-
15. 计算:16. △ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
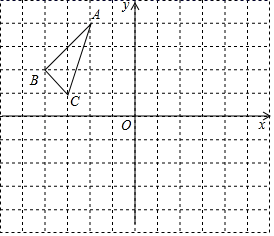 (1)、画出△ABC关于原点O的中心对称图形△A1B1C1;(2)、画出将△ABC绕点C顺时针旋转90°得到△A2B2C2 .(3)、在(2)的条件下,求点A旋转到点A2所经过的路线长(结果保留π).17. 下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN , DM , CB为三根垂直于AB的支柱,垂足分别为N , M , B , ∠EAB=31°,DF⊥BC于点F , ∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)
(1)、画出△ABC关于原点O的中心对称图形△A1B1C1;(2)、画出将△ABC绕点C顺时针旋转90°得到△A2B2C2 .(3)、在(2)的条件下,求点A旋转到点A2所经过的路线长(结果保留π).17. 下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN , DM , CB为三根垂直于AB的支柱,垂足分别为N , M , B , ∠EAB=31°,DF⊥BC于点F , ∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)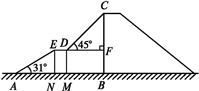 18. 有4张看上去无差别的卡片,上面分别写着1,2,3,4.(1)、一次性随机抽取2张卡片,求这两张卡片上的数字之和为奇数的概率;(2)、随机摸取1张后,放回并混在一起,再随机抽取1张,求两次取出的卡片上的数字之和等于4的概率.19. 已知AB为⊙O的直径,点C为⊙O上一点,点D为AB延长线一点,连接AC .
18. 有4张看上去无差别的卡片,上面分别写着1,2,3,4.(1)、一次性随机抽取2张卡片,求这两张卡片上的数字之和为奇数的概率;(2)、随机摸取1张后,放回并混在一起,再随机抽取1张,求两次取出的卡片上的数字之和等于4的概率.19. 已知AB为⊙O的直径,点C为⊙O上一点,点D为AB延长线一点,连接AC . (1)、如图①,OB=BD , 若DC与⊙O相切,求∠D和∠A的大小;(2)、如图②,CD与⊙O交于点E , AF⊥CD于点F连接AE , 若∠EAB=18°,求∠FAC的大小.20.
(1)、如图①,OB=BD , 若DC与⊙O相切,求∠D和∠A的大小;(2)、如图②,CD与⊙O交于点E , AF⊥CD于点F连接AE , 若∠EAB=18°,求∠FAC的大小.20.如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
 (1)、求证:△ABM∽△EFA;
(1)、求证:△ABM∽△EFA;
(2)、若AB=12,BM=5,求DE的长.21. 已知二次函数y=mx2+(1﹣2m)x+1﹣3m .(1)、当m=2时,求二次函数图象的顶点坐标;(2)、已知抛物线与x轴交于不同的点A、B .①求m的取值范围;
②若3≤m≤4时,求线段AB的最大值及此时二次函数的表达式.
22. 某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.(1)、当销售单价为70元时,每天的销售利润是多少?(2)、求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量x的取值范围;(3)、如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)23. 如图,矩形ABCD(AB>AD)中,点M是边DC上的一点,点P是射线CB上的动点,连接AM , AP , 且∠DAP=2∠AMD . (1)、若∠APC=76°,则∠DAM=;(2)、猜想∠APC与∠DAM的数量关系为 , 并进行证明;(3)、如图1,若点M为DC的中点,求证:2AD=BP+AP;(4)、如图2,当∠AMP=∠APM时,若CP=15, = 时,则线段MC的长为 .
(1)、若∠APC=76°,则∠DAM=;(2)、猜想∠APC与∠DAM的数量关系为 , 并进行证明;(3)、如图1,若点M为DC的中点,求证:2AD=BP+AP;(4)、如图2,当∠AMP=∠APM时,若CP=15, = 时,则线段MC的长为 .