安徽省合肥市瑶海区2020年中考数学二模试卷
试卷更新日期:2020-07-09 类型:中考模拟
一、单选题
-
1. 在﹣3、0、 、3中,最大的数是( )A、﹣3 B、0 C、 D、32. 下列计算正确的是( )A、2×32=36 B、(﹣2a2b3)3 =﹣6a6b9 C、﹣5a5b3c÷15a4b=﹣3ab2c D、(a﹣2b)2 =a2﹣4ab+4b23. 某集成电路制造有限公司已于2019年第三季度成功量产了第一代14纳米FinFET工艺,这是国内第一条14nm工艺生产线,已知14nm为0.000000014米,数据0.000000014用科学记数法表示为( )A、1.4× B、1.4× C、14× D、1.4×4. 下列图形都是由大小相同的正方体搭成的,其三视图都相同的是( )A、
 B、
B、 C、
C、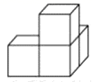 D、
D、 5. 如图,点A、B分别在直线a、b上,且直线a∥b,以点A为圆心,AB长为半径画弧交直线a于点C,连接BC,若∠2=67°,则∠1=( )
5. 如图,点A、B分别在直线a、b上,且直线a∥b,以点A为圆心,AB长为半径画弧交直线a于点C,连接BC,若∠2=67°,则∠1=( ) A、78° B、67° C、46° D、23°6. 如表是某班所有同学一周体育锻炼时间的统计情况,请通过表格中的数据可得该班级同学一周参加体育锻炼时间的众数与中位数分别是( )
A、78° B、67° C、46° D、23°6. 如表是某班所有同学一周体育锻炼时间的统计情况,请通过表格中的数据可得该班级同学一周参加体育锻炼时间的众数与中位数分别是( )锻炼时间(小时)
7
8
9
10
人数(人)
3
16
14
7
A、8与9 B、8与8.5 C、16与8.5 D、16与10.57. 已知点(a,m),(b,n)在反比例函数y=﹣ 的图象上,且a>b,则( )A、m>n B、m<n C、m=n D、m、n的大小无法确定8. 在边长为2的正方形ABCD中,点E是AD边上的中点,BF平分∠EBC交CD于点F,过点F作FG⊥AB交BE于点H,则GH的长为( )A、 B、 C、 D、9. 如图所示,在△ABC中,AB=AC,动点D在折线段BAC上沿B→A→C方向以每秒1个单位的速度运动,过D垂直于BC的直线交BC边于点E.如果AB=5,BC=8,点D运动的时间为t秒,△BDE的面积为S,则S关于t的函数图象的大致形状是( )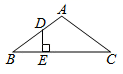 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,菱形ABCD的边长为2 ,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )
10. 如图,菱形ABCD的边长为2 ,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )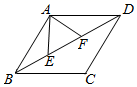 A、4 B、4+ C、2+2 D、6
A、4 B、4+ C、2+2 D、6二、填空题
-
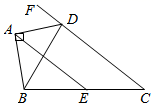
11. 分解因式:3a3- 12a =.12. 命题:“如果|a|=|b|,那么a=b”的逆命题是:(填“真命题”或“假命题”).13. 如图,四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE= .
 14. 如果二次函数y=x2+b(b为常数)与正比例函数y=2x的图象在﹣1≤x≤2时有且只有一个公共交点,那么常数b的值应为 .
14. 如果二次函数y=x2+b(b为常数)与正比例函数y=2x的图象在﹣1≤x≤2时有且只有一个公共交点,那么常数b的值应为 .三、解答题
-
15. 计算:2•sin30°+|﹣ |+(﹣ )﹣1﹣ .16. 如图,已知A(﹣3,3)、B(﹣4,1)、C(﹣1,1)是平面直角坐标系上的三点.
 (1)、请画出△ABC绕点O逆时针旋转90°后的△A1B1C1;(2)、请画出△A1B1C1关于y轴对称△A2B2C2;(3)、判断以A、A1、A2为顶点的三角形的形状.(无需说明理由)17. 新型冠状病毒肺炎疫情发生后,全社会的积极参与疫情防控工作下,才有了我们的平安复学.为了能在复学前将一批防疫物资送达校园,某运输公司组织了甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20箱防疫物资,且甲种货车装运900箱防疫物资所用车辆与乙种货车装运600箱防疫物资所用的车辆相等,求甲、乙两种货车每辆车可装多少箱防疫物资?18. 化简: + +…+ .
(1)、请画出△ABC绕点O逆时针旋转90°后的△A1B1C1;(2)、请画出△A1B1C1关于y轴对称△A2B2C2;(3)、判断以A、A1、A2为顶点的三角形的形状.(无需说明理由)17. 新型冠状病毒肺炎疫情发生后,全社会的积极参与疫情防控工作下,才有了我们的平安复学.为了能在复学前将一批防疫物资送达校园,某运输公司组织了甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20箱防疫物资,且甲种货车装运900箱防疫物资所用车辆与乙种货车装运600箱防疫物资所用的车辆相等,求甲、乙两种货车每辆车可装多少箱防疫物资?18. 化简: + +…+ .为了能找到复杂计算问题的结果,我们往往会通过将该问题分解,试图找寻算式中每个式子是否存在某种共同规律,然后借助这个规律将问题转化为可以解决的简单问题.下面我们尝试着用这个思路来解决上面的问题.请你按照这个思路继续进行下去,并把相应横线上的空格补充完整.
(1)、(分析问题)第1个加数: = ﹣ ;第2个加数: = ﹣ ;
第3个加数: = ﹣ ;
第4个加数:= ﹣ ;
(2)、(总结规律)第n个加数:=﹣ .(3)、(解决问题)请你利用上面找到的规律,继续化简下面的问题.(结果只需化简,无需求出最后得数) + +…+ .19. 寿春路桥(如图①)横跨合肥市母亲河﹣南淝河,它位于合肥市东西交通主干道寿春路上,建成于1987年年底,为中承式钢筋砼(tong)拱桥,桥的上部结构为2个钢筋混凝土半月形拱肋,如图②是桥拱肋的简化示意图,其中拱宽(弦AB)约100米. (1)、在图②中,请你用尺规作图的方法首先找出弧AB所在圆的圆心O,然后确定弧AB、弦AB的中点C、D.(不要写作法,但保留作图痕迹)(2)、在图②中,若∠AOB=80°,求该拱桥高CD约为多少米?(结果精确到0.1米,参考数据:sin50°≈0.77,cos50°≈0.6,tan50°≈1.19)20. 如图,已知两个全等的等腰三角形如图所示放置,其中顶角顶点(点A)重合在一起,连接BD和CE,交于点F.
(1)、在图②中,请你用尺规作图的方法首先找出弧AB所在圆的圆心O,然后确定弧AB、弦AB的中点C、D.(不要写作法,但保留作图痕迹)(2)、在图②中,若∠AOB=80°,求该拱桥高CD约为多少米?(结果精确到0.1米,参考数据:sin50°≈0.77,cos50°≈0.6,tan50°≈1.19)20. 如图,已知两个全等的等腰三角形如图所示放置,其中顶角顶点(点A)重合在一起,连接BD和CE,交于点F.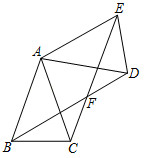 (1)、求证:BD=CE;(2)、当四边形ABFE是平行四边形时,且AB=2,∠BAC=30°,求CF的长.21. 央视举办的《中国诗词大会》受到广大学生群体广泛关注.某校的诗歌朗诵社团就《中国诗词大会》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中说给信息解答下列问题:
(1)、求证:BD=CE;(2)、当四边形ABFE是平行四边形时,且AB=2,∠BAC=30°,求CF的长.21. 央视举办的《中国诗词大会》受到广大学生群体广泛关注.某校的诗歌朗诵社团就《中国诗词大会》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中说给信息解答下列问题: (1)、本次被调查对象共有人,扇形统计图中被调查者“非常喜欢”等级所对应圆心角的度数为;(2)、将条形统计图补充完整,并标明数据;(3)、若选“不太喜欢”的人中有两名女生,其余是男生,从原“不太喜欢”的人中挑选两名学生了解不太喜欢的原因,请用画树状图或列表法求所选取的这两名学生恰好是一男一女的概率.22. 随着时代的不断发展,新颖的网络购进逐渐融入到人们的生活中,“拼一拼”电商平台上提供了一种拼团购买方式,当拼团(单数不超过15单)成功后商家将会让利一定的额度给予顾客实惠.现在某商家准备出手一种每件成本25元/件的新产品,经市场调研发现,单价y(单位:元)、日销售量m(单位:件)与拼单数x(单位:单)之间存在着如表的数量关系:
(1)、本次被调查对象共有人,扇形统计图中被调查者“非常喜欢”等级所对应圆心角的度数为;(2)、将条形统计图补充完整,并标明数据;(3)、若选“不太喜欢”的人中有两名女生,其余是男生,从原“不太喜欢”的人中挑选两名学生了解不太喜欢的原因,请用画树状图或列表法求所选取的这两名学生恰好是一男一女的概率.22. 随着时代的不断发展,新颖的网络购进逐渐融入到人们的生活中,“拼一拼”电商平台上提供了一种拼团购买方式,当拼团(单数不超过15单)成功后商家将会让利一定的额度给予顾客实惠.现在某商家准备出手一种每件成本25元/件的新产品,经市场调研发现,单价y(单位:元)、日销售量m(单位:件)与拼单数x(单位:单)之间存在着如表的数量关系:拼单数x(单位:单)
2
4
8
12
单价y(单位:元)
34.50
34.00
33.00
32.00
日销售量m(单位:件)
68
76
92
108
请根据以上提供的信息解决下列问题:
(1)、请直接写出单价y和日销售量m分别与拼单数x之间的一次函数关系式;(2)、拼单数设置为多少单时的日销售利润最大,最大的销售利润是多少?(3)、在实际销售过程中,厂家希望能有更多的商品出售,因此对电商每销售一件商品厂家就给予电商补助a元(a≤2),那么电商在获得补助之日后日销售利润能够随单数x的增大而增大,那么a的取值范围是什么?23. 如图,在等边△ABC中,BD=CE,连接AD、BE交于点F. (1)、求∠AFE的度数;(2)、求证:AC•DF=BD•BF;(3)、连接FC,若CF⊥AD时,求证:BD= DC.
(1)、求∠AFE的度数;(2)、求证:AC•DF=BD•BF;(3)、连接FC,若CF⊥AD时,求证:BD= DC.