安徽合肥蜀山区2020年中考数学一模试卷
试卷更新日期:2020-07-09 类型:中考模拟
一、单选题
-
1. -2020的倒数是( )A、2020 B、-2020 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 2019年,全国实行地区生产总值统一核算改革,某城区 约为1004.2亿元,第一次进入千亿城区,将数据1004.2亿用科学记数法表示为( )A、 B、 C、 D、4. 如图是由大小相同的5个小正方体组成的几何体,该几何体的俯视图是( )
 A、
A、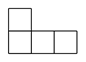 B、
B、 C、
C、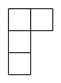 D、
D、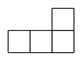 5. 一位射击运动员在一次训练效果测试中射击了10次,成绩如图所示,对于这10次射击的成绩有如下结论,其中错误的是( )
5. 一位射击运动员在一次训练效果测试中射击了10次,成绩如图所示,对于这10次射击的成绩有如下结论,其中错误的是( ) A、众数是 B、中位数是 C、平均数是 D、方差是6. 如图,在矩形 ABCD 中放置了一个直角三角形 EFG , 被 AD 平分,若 ,则 的度数为( )
A、众数是 B、中位数是 C、平均数是 D、方差是6. 如图,在矩形 ABCD 中放置了一个直角三角形 EFG , 被 AD 平分,若 ,则 的度数为( )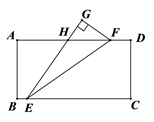 A、 B、 C、 D、7. 关于方程 根的情况,下列判断正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根8. “半日走遍江淮大地,安徽风景尽在徽园”,位于省会合肥的徽园景点某年三月共接待游客m万人,四月比三月旅游人数增加了15%,五月比四月游客人数增加了a%,已知三月至五月徽园的游客人数平均月增长率为20%,则可列方程为( )A、 B、 C、 D、9. 如图, 是 的外接圆, 的半径 , ,则弦 的长为( )
A、 B、 C、 D、7. 关于方程 根的情况,下列判断正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根8. “半日走遍江淮大地,安徽风景尽在徽园”,位于省会合肥的徽园景点某年三月共接待游客m万人,四月比三月旅游人数增加了15%,五月比四月游客人数增加了a%,已知三月至五月徽园的游客人数平均月增长率为20%,则可列方程为( )A、 B、 C、 D、9. 如图, 是 的外接圆, 的半径 , ,则弦 的长为( )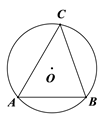 A、2.4 B、3.2 C、3 D、510. 二次函数y=x2+px+q,当0≤x≤1时,此函数最大值与最小值的差( )A、与p、q的值都有关 B、与p无关,但与q有关 C、与p、q的值都无关 D、与p有关,但与q无关
A、2.4 B、3.2 C、3 D、510. 二次函数y=x2+px+q,当0≤x≤1时,此函数最大值与最小值的差( )A、与p、q的值都有关 B、与p无关,但与q有关 C、与p、q的值都无关 D、与p有关,但与q无关二、填空题
-
11. 化简: .12. 某中学为了了解八年级女生的体能情况,随机抽取了部分女生进行了跳绳测试,按成绩分为优秀、良好、合格与不合格四个等级,绘制了如下的统计图,则不合格人数在扇形统计图中对应的圆心角为度.
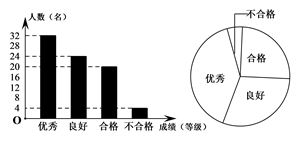 13. 如图所示,南宋数学家杨辉在《详解九章算法》中出现的三角形状的数阵,又称为“杨辉三角形”.该三角形中的数据排列有着一定的规律,按此规律排列下去,第100行的左边第3个数是 .
13. 如图所示,南宋数学家杨辉在《详解九章算法》中出现的三角形状的数阵,又称为“杨辉三角形”.该三角形中的数据排列有着一定的规律,按此规律排列下去,第100行的左边第3个数是 .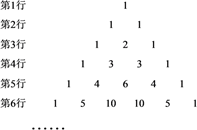 14. 如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,点E、F分别是边AC、BC上的动点,且EF//AB,点C关于EF的对称点D恰好落在△ABC的内角平分线上,则CD长为 .
14. 如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,点E、F分别是边AC、BC上的动点,且EF//AB,点C关于EF的对称点D恰好落在△ABC的内角平分线上,则CD长为 .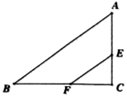
三、解答题
-
15. 解不等式:16. 《九章算术》是中国传统数学最重要的著作之一,其中《均输》卷记载了一道有趣的数学问题:“今有凫(注释:野鸭)起南海,九日至北海;雁起北海,六日至南海.今凫雁俱起,问何日相逢?”译文:“野鸭从南海起飞, 9 天飞到北海;大雁从北海起飞, 6 天飞到南海.现野鸭与大雁分别从南海和北海同时起飞,问经过多少天相遇?请列方程解答上面问题.17. 如图,在边长为1个单位长度的小正方形组成的12×12的网格中,已知点O、A、B均为格点.
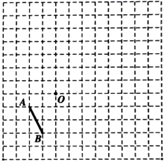 (1)、在给定的网格中,以点O为位似中心将线段AB放大为原来的2倍,得到线段A´B´.(点A、B的对应点分别为点A´、B´),画出线段A´B´.(2)、以线段A´B´为一边,作一个格点四边形A´B´CD,使得格点四边形A´B´CD是轴对称图形(作出一个格点四边形即可)18. 为了考查学生的综合素质,某市决定:九年级毕业生统一参加中考实验操作考试,根据今年的实际情况,中考实验操作考试科目为: (物理)、 (化学)、 (生物),每科试题各为 道,考生随机抽取其中 道进行考试.小明和小丽是某校九年级学生,需参加实验考试.(1)、小明抽到化学实验的概率为;(2)、若只从考试科目考虑,小明和小丽抽到不同科目的概率为多少?19. 某校数学兴趣小组假期实地测量南淝河两岸互相平行的一段东西走向的河的宽度,在河的南岸边点 处,测得河的北岸边点 在其东北方向,然后向南走 米到达点 处,测得点 在点 的北偏东 方向上.
(1)、在给定的网格中,以点O为位似中心将线段AB放大为原来的2倍,得到线段A´B´.(点A、B的对应点分别为点A´、B´),画出线段A´B´.(2)、以线段A´B´为一边,作一个格点四边形A´B´CD,使得格点四边形A´B´CD是轴对称图形(作出一个格点四边形即可)18. 为了考查学生的综合素质,某市决定:九年级毕业生统一参加中考实验操作考试,根据今年的实际情况,中考实验操作考试科目为: (物理)、 (化学)、 (生物),每科试题各为 道,考生随机抽取其中 道进行考试.小明和小丽是某校九年级学生,需参加实验考试.(1)、小明抽到化学实验的概率为;(2)、若只从考试科目考虑,小明和小丽抽到不同科目的概率为多少?19. 某校数学兴趣小组假期实地测量南淝河两岸互相平行的一段东西走向的河的宽度,在河的南岸边点 处,测得河的北岸边点 在其东北方向,然后向南走 米到达点 处,测得点 在点 的北偏东 方向上. (1)、求 的度数;(2)、求出这段河的宽度.(结果精确到1米,参考数据: , )20. 如图,已知反比例函数 (k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C , 若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
(1)、求 的度数;(2)、求出这段河的宽度.(结果精确到1米,参考数据: , )20. 如图,已知反比例函数 (k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C , 若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.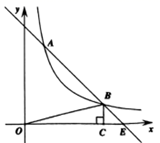 (1)、求反比例函数、一次函数的表达式及直线AB与x轴交点E的坐标;(2)、已知点D(t , 0)(t>0),过点D作垂直于x轴的直线,在第一象限内与一次函数y=-x+b的图像相交于点P , 与反比函数 上的图像相交于点Q , 若点P位于点Q的上方,请结合函数图象直接写出此时t的取值范围.21. 如图,四边形ABCD内接于⊙O,AC为直径,点D为弧ACB的中点,过点D的切线与BC的延长线交于点E.
(1)、求反比例函数、一次函数的表达式及直线AB与x轴交点E的坐标;(2)、已知点D(t , 0)(t>0),过点D作垂直于x轴的直线,在第一象限内与一次函数y=-x+b的图像相交于点P , 与反比函数 上的图像相交于点Q , 若点P位于点Q的上方,请结合函数图象直接写出此时t的取值范围.21. 如图,四边形ABCD内接于⊙O,AC为直径,点D为弧ACB的中点,过点D的切线与BC的延长线交于点E.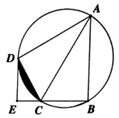 (1)、用尺规作图作出圆心O;(保留作图痕迹,不写作法);(2)、求证:DE⊥BC;(3)、若OC=2CE=4,求图中阴影部分面积.22. 某水果连锁店销售某种热带水果,其进价为20元/千克.销售一段时间后发现:该水果的日销量y(千克)与售价x(元/千克)的函数关系如图所示:
(1)、用尺规作图作出圆心O;(保留作图痕迹,不写作法);(2)、求证:DE⊥BC;(3)、若OC=2CE=4,求图中阴影部分面积.22. 某水果连锁店销售某种热带水果,其进价为20元/千克.销售一段时间后发现:该水果的日销量y(千克)与售价x(元/千克)的函数关系如图所示: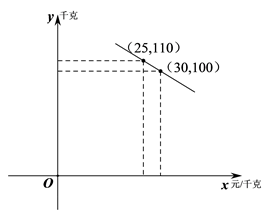 (1)、求y关于x的函数解析式;(2)、当售价为多少元/千克时,当日销售利润最大,最大利润为多少元?(3)、由于某种原因,该水果进价提高了 元/千克( ),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是 元,请直接写出 的值.23. 如图,在△ABC中,∠ACB=90°,AC=BC,CD是AB边上的中线,点E为线段CD上一点(不与点C、D重合),连接BE,作EF⊥BE与AC的延长线交于点F,与BC交于点G,连接BF.
(1)、求y关于x的函数解析式;(2)、当售价为多少元/千克时,当日销售利润最大,最大利润为多少元?(3)、由于某种原因,该水果进价提高了 元/千克( ),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是 元,请直接写出 的值.23. 如图,在△ABC中,∠ACB=90°,AC=BC,CD是AB边上的中线,点E为线段CD上一点(不与点C、D重合),连接BE,作EF⊥BE与AC的延长线交于点F,与BC交于点G,连接BF.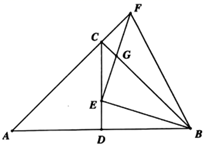 (1)、求证:△CFG∽△EBG;(2)、求∠EFB的度数;(3)、求 的值;
(1)、求证:△CFG∽△EBG;(2)、求∠EFB的度数;(3)、求 的值;