苏教版高中数学必修一2.2函数的简单性质
试卷更新日期:2020-07-08 类型:同步测试
一、单选题
-
1. 下列函数在 上是增函数的是( )A、
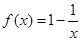 B、
B、 C、
C、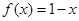 D、
D、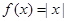 2. 下列函数中,既是奇函数,又在 上为增函数的是( )A、
2. 下列函数中,既是奇函数,又在 上为增函数的是( )A、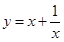 B、
B、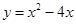 C、
C、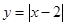 D、
D、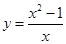 3. 已知函数 在 上为奇函数,且当 时, ,则 ( )
3. 已知函数 在 上为奇函数,且当 时, ,则 ( )
A、-3 B、-1 C、1 D、24. 已知函数f(x)是定义在[1,4]上的减函数,且f(m)>f(4﹣m),则实数m的取值范围是( )A、(2,3] B、[1,2) C、(﹣∞,2) D、(2,+∞)5. 已知 是定义域为 的奇函数,满足 。若 ,则 ( )A、-50 B、0 C、2 D、506. 已知函数f(x)=m·2x+x+m2-2,若存在实数x,满足f(-x)=-f(x),则实数m的取值范围为( )A、(-∞,-2]U(0,1] B、[-2,0)U(0,1] C、[-2,0)U[1,+∞) D、(-∞,-2]U[1,+∞)7. 已知f(x)是定义域为R的偶函数,当x≤0时,f(x)=x2﹣2x,那么不等式f(x+1)>3的解集是( )A、(﹣∞,2)∪(2,+∞) B、(﹣∞,﹣2)∪(0,+∞) C、(﹣∞,0)∪(2,+∞) D、(﹣∞,﹣1)∪(1,+∞)8. 偶函数在区间[0,4]上单调递减,则有( )A、 B、 C、 D、9. 已知 是定义域为 的奇函数,满足 .若 ,则 ( )A、-2018 B、0 C、2 D、5010. 已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f(x)≥0,f(x)是增函数,则a=f(2010),b=f( ),c=﹣f( )的大小关系是( )A、b<c<a B、c<b<a C、a<c<b D、a<b<c二、填空题
-
11. 若函数 是奇函数,则 =( )A、2 B、 C、3 D、412. 已知函数f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a﹣1,2a],则( )A、 ,b=0 B、a=﹣1,b=0 C、a=1,b=1 D、a= ,b=﹣113. 已知定义在R上的偶函数f(x)在[0,+∞)单调递增,且f(1)=0,则不等式f(x﹣2)≥0的解集是 .14. 若函数 是偶函数,则 等于.15. 已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2+2x,若f(2﹣a2)>f(a),则实数a的取值范围是 .
三、解答题
-
16. 判断函数f(x)= 在区间(1,+∞)上的单调性,并用单调性定义证明.17. 已知f(x)=8+2x﹣x2 , g(x)=f(2﹣x2),试求g(x)的单调区间.18. 已知定义在[﹣3,3]上的函数y=f(x)是增函数.
(1)若f(m+1)>f(2m﹣1),求m的取值范围;
(2)若函数f(x)是奇函数,且f(2)=1,解不等式f(x+1)+1>0.