初中数学人教版七年级下册 平行线的性质
试卷更新日期：2020-07-08 类型：复习试卷
一、单选题
-
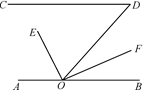
1. 如图， 中，∠ACB=90°，DE 过点C ， 且DE∥AB，若∠ACD=65°，则∠B的度数是（ ）
A、25° B、35° C、45° D、55°2. 如图，若AB∥CD，CD∥EF，那么∠BCE＝（ ）
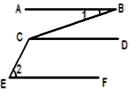A、∠1＋∠2 B、∠2－∠1 C、180°－∠1＋∠2 D、180°－∠2＋∠13. 一个学员在广场上驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是（ ）A、第一次向右拐 50° ，第二次向左拐130° B、第一次向右拐 50° ，第二次向右拐130° C、第一次向左拐 50° ，第二次向左拐130° D、第一次向左拐 30° ，第二次向右拐 30°4. 如图，直线 ，三角板的直角顶点放在直线 上，两直角边与直线 相交，如果 ，那么 等于（ ）
A、 B、 C、 D、5. 如图是一块断尺，一块等腰直角三角板的直角顶点刚好落在断尺的下端.则下列结论中，不正确的是（ ）
A、∠1+∠3＝90° B、∠5﹣∠2＝90° C、∠2+∠3+∠4+∠5＝270° D、∠5﹣∠3＝90°6. 将一直角三角尺与两边平行的纸条按如图所示放置，下列结论：
①∠1=∠2；②∠3=∠4；③∠2+∠4=90°；④∠4+∠5=180°.正确的个数是（ ）
A、1 B、2 C、3 D、47. 如图，一副直角三角板按如图所示的方式摆放，其中点 在 的延长线上，且AB∥FC，则 的度数为（ ）
A、15° B、30° C、45° D、60°8. 如图，AB∥CD，∠EAF=3∠BAF，∠ECF=3∠DCF，则∠E与∠F的数量关系是（ ）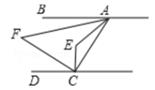
A、∠E+∠F=180° B、∠E=3∠F C、∠E-∠F=90° D、∠E=4∠F9. 如图，已知A1B∥AnC，则∠A1＋∠A2＋…＋∠An等于（ ）
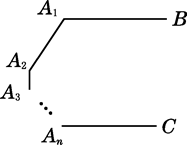A、180°n B、(n＋1)·180° C、(n－1)·180° D、(n－2)·180°10. 如图，AB∥CD∥EF，则下列各式中正确的是（ ）
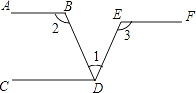A、∠1=180°﹣∠3 B、∠1=∠3﹣∠2 C、∠2+∠3=180°﹣∠1 D、∠2+∠3=180°+∠1二、填空题
-
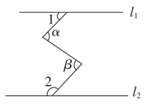
11. 如图，若直线 ， ， ，则 的度数为 ．
12. 如图，直线EF分别交AB、CD于点E，F，且AB∥CD，若∠1=60°，则∠2=°.
13. 如图，一副三角板GEF和HEF按如图所示放置，过E的直线AB与过F的直线CD相互平行，若∠CFG＝72°，则∠BEH＝°．
14. 若∠A的两边与∠B的两边分别平行，∠A比∠B的3倍小60°，则∠B＝.15. 若∠α与∠β的两边分别平行，且∠a=(2x+10)°，∠β=(3x-20)°，则∠a的度数为。16. 如图：直线l1∥l2 ， 一块含30°角的直角三角板如图所示放置，∠1=25°，则∠2=.
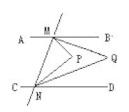
17. 已知∠A与∠B(∠A，∠B都是大于0°且小于180°的角)的两边一边平行，另一边垂直，且2∠A-∠B=18°，则∠A的度数为。18. 如图，直线12∥12 ， ∠A=125°，∠B=85°，则∠1+∠2=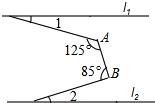
19. 如图，已知EF∥GH，A、D为GH上的两点，M、B为EF上的两点，延长AM于点C，AB平分∠DAC，直线DB平分∠FBC，若∠ACB=100°，则∠DBA的度数为 ．
20.如图，直线a∥b ， ∠1=125°，则∠2的度数为°.
三、解答题
-
21. 如图，如果 ， ，那么 吗？说说你的理由．
22. 已知：如图， ∥ ，∠1=55°，∠2=40°，求∠3和∠4的度数
23. 如图，EF∥BC，AC平分∠BAF，∠B=80°.求∠C的度数.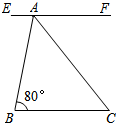
24. 如图所示，AB∥CD∥EF ， ∠ABC＝55°，∠CEF＝150°，求∠BCE的度数．
