吉林省延边州2020年中考数学模拟试卷
试卷更新日期:2020-07-07 类型:中考模拟
一、单项选择题
-
1. 下列数中,比 小的数是( )A、 B、 C、0 D、22. 截止到2020年5月20日,全世界新冠病确诊患者已超过4980000名,将4980000用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,射线 , 分别与直线 交于点 , .现将射线 沿直线 向右平移过点 ,若 , ,则 的度数为( )
 A、 B、 C、 D、5. 如图, 与 切于点 , , 是 上一点,连接 并延长与 交于点 ,连接 ,
A、 B、 C、 D、5. 如图, 与 切于点 , , 是 上一点,连接 并延长与 交于点 ,连接 ,, ,则 的长为( )
 A、 B、 C、 D、6. 如图,大正方体上面正中间放置小正方体,小正方体6个表面写了数字1到6,且所相对面两个数字之和都是7,则这个几何体的左视图为( )
A、 B、 C、 D、6. 如图,大正方体上面正中间放置小正方体,小正方体6个表面写了数字1到6,且所相对面两个数字之和都是7,则这个几何体的左视图为( ) A、
A、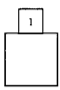 B、
B、 C、
C、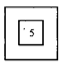 D、
D、
二、填空题
-
7. 计算: .8. 有意义,则 的取值范围.9. 计算: .10. 分式方程 的解是.11. 抛物线 与 轴有两个交点,则原点左侧交点坐标为.12. 如图,在矩形 中, 是对角线,延长 到 ,使 ,连接 .若 ,则 度.
 13. 如图,在 中, , , . 是边 上一点, ,以 为一边向上作正三角形 , 、 与 分别交于点 、 ,则线段 的长为.
13. 如图,在 中, , , . 是边 上一点, ,以 为一边向上作正三角形 , 、 与 分别交于点 、 ,则线段 的长为. 14. 如图,在 中, ,点 的坐标为 ,点 在 轴上, 轴.将 沿 翻折得到 ,直线 过点 ,则四边形 的面积为.
14. 如图,在 中, ,点 的坐标为 ,点 在 轴上, 轴.将 沿 翻折得到 ,直线 过点 ,则四边形 的面积为.
三、解答题
-
15. 先化简,再求值.
,其中 .
16. 某班去看演出,甲种票每张24元,乙种票每张18元,如果35名学生购票恰好用去750元,甲乙两种票各买了多少张?17. 甲、乙两个不透明的盒子中分别装有三个标有数字的小球,小球除数字不同外,其余均相同.甲盒中三个小球上分别标有数字1、2、7,乙盒中三个小球上分别标有数字4、5、6.小明分别从甲、乙两个盒子中随机摸出一个小球,用画树状图(或列表)的方法,求小明摸出的两个小球上的数字之和为4的倍数的概率. 18. 如图,四边形 是平行四边形, 是边 上一点,且 .过点 , 分别作 , .求证: .
18. 如图,四边形 是平行四边形, 是边 上一点,且 .过点 , 分别作 , .求证: .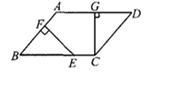
四、解答题
-
19. 某学校为了解九年级学生线上教学中所学知识情况,随机抽出一部分九年级学生进行了质量检测,其成绩结果分三类:A:优秀B:及格C:不及格,然后根据结果做了不完全的条形图和扇形图,如图所示.
 (1)、这次被抽出的学生是名.(2)、完成直方图.(3)、该学校九年级学生有200名,通过计算,估计九年级不及格学生人数.20. 如图均是5×5的正方形网络,每个小正方形的顶点称为格点, 的顶点 , , 都在格点上,按照下列要求画图.
(1)、这次被抽出的学生是名.(2)、完成直方图.(3)、该学校九年级学生有200名,通过计算,估计九年级不及格学生人数.20. 如图均是5×5的正方形网络,每个小正方形的顶点称为格点, 的顶点 , , 都在格点上,按照下列要求画图. (1)、在图1中,画 的高 .(2)、在图2中,① ;
(1)、在图1中,画 的高 .(2)、在图2中,① ;②画以 为顶角的等腰三角形 ,使点 在格点上 .
(3)、在图3中,画出 的角平分线 .(要求:只用直尺,不能用圆规,不要求写出画法)
21. 如图,海面上 , 两岛分别位于 岛的正东和正北方向.一艘船从 岛出发以16海里 的速度向正北方向航行2小吋到达 岛,此吋测得 岛在 岛的南偏东 .求 , 两岛之间的距离.(结果精确到0.1海里)(参考数据: , , )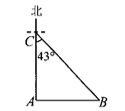 22. 如图,点 ,点 , , 分别是 , 的中点,连接 .将 绕点 逆时针方向旋转 ,得到 .双曲线 过线段 的中点 .
22. 如图,点 ,点 , , 分别是 , 的中点,连接 .将 绕点 逆时针方向旋转 ,得到 .双曲线 过线段 的中点 . (1)、 .(2)、点 的横坐标为(3)、求双曲线的解析式.
(1)、 .(2)、点 的横坐标为(3)、求双曲线的解析式.五、解答题
-
23. 甲车从 地出发向 地匀速行驶,甲出发1小时后乙车从 地出发沿同一条路向 地匀速行驶.两车相遇后乙车立即以原来速度返回 地,甲车继续以原来速度行驶到 地.甲、乙两车之间的距离 与甲车的行驶时间 之间的函数图象如图所示.
 (1)、甲车的速度是 ;(2)、求出乙车开始出发到与甲车第一次相遇时, 与 的函数关系式,并写出自变量的取值范围。(3)、直接写出 的值.24. 在矩形纸片 中,点 , 分别为边 , 的中点,点 , 分别在边 , 上,且 .将 沿 折叠,点 的对应点为点 ,将 沿 折叠,点 的对应点为点 .
(1)、甲车的速度是 ;(2)、求出乙车开始出发到与甲车第一次相遇时, 与 的函数关系式,并写出自变量的取值范围。(3)、直接写出 的值.24. 在矩形纸片 中,点 , 分别为边 , 的中点,点 , 分别在边 , 上,且 .将 沿 折叠,点 的对应点为点 ,将 沿 折叠,点 的对应点为点 .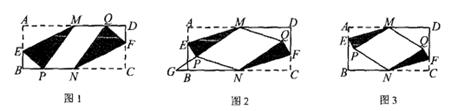 (1)、如图1,若点 , 分别落在边 , 上,则四边形 的形状是.(2)、如图2,若点 , 均落在矩形 内部,直线 与直线 交于点 ,其它条件不变,则第(1)小题的结论是否仍然成立?说明其理由.(3)、如图3,若 , ,当四边形 为菱形时,直接写出 的长度.
(1)、如图1,若点 , 分别落在边 , 上,则四边形 的形状是.(2)、如图2,若点 , 均落在矩形 内部,直线 与直线 交于点 ,其它条件不变,则第(1)小题的结论是否仍然成立?说明其理由.(3)、如图3,若 , ,当四边形 为菱形时,直接写出 的长度.六、解答题
-
25. 如图,在 中, , , , 是中线.点 从点 出发以
速度沿折线 匀速运动,到点 停止运动.过点 作 ,垂足为点 ,以 为一边作矩形 ,且 .点 , 始终位于 的异侧,矩形 与 的重叠部分面积为 ,点 的运动时间为 .
 (1)、当点 在边 上时, .(2)、求 与 之间的函数关系式.(3)、当矩形 与 的重叠部分为轴对称图形时,直接写出 的取值范围.26. 如图,点 ,点 ,点 、 关于原点 的对称点分别为点 、 .线段 沿 轴向下平移 个单位长度,得到线段 ,抛物线 过点 , .
(1)、当点 在边 上时, .(2)、求 与 之间的函数关系式.(3)、当矩形 与 的重叠部分为轴对称图形时,直接写出 的取值范围.26. 如图,点 ,点 ,点 、 关于原点 的对称点分别为点 、 .线段 沿 轴向下平移 个单位长度,得到线段 ,抛物线 过点 , . (1)、当 时, ;(2)、求 与 之间的关系式;(3)、线段 沿y轴向下平移 个单位长度,得到线段 ,抛物线 过点 , .
(1)、当 时, ;(2)、求 与 之间的关系式;(3)、线段 沿y轴向下平移 个单位长度,得到线段 ,抛物线 过点 , .;(用含 的式子来表示)
与 之间的关系式为 ;
(4)、点 在 轴上,当 为等腰直角三角形时,直接写出点 的坐标.