广东省深圳市南山区育才二中2020年中考数学二模试卷
试卷更新日期:2020-07-07 类型:中考模拟
一、选择题(每题3分,共36分)
-
1. 在实数0, , , 中,最小的数是( )A、0 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 改革开放以来,我国众多科技实体在各自行业取得了举世瞩目的成就,大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表.上述四个企业的标志是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 新冠病毒(2019-nCoV)是一种新的冠状病毒,它是一类具有囊膜的正链单股RNA病毒,其遗传性物质是所有RNA病毒中最大的,也是自然界广泛存在的一大类病毒.其粒子形状不规则,平均直径为100nm(纳米).1纳米= ,100纳米可以表示为( )米A、 B、 C、 D、5. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
4. 新冠病毒(2019-nCoV)是一种新的冠状病毒,它是一类具有囊膜的正链单股RNA病毒,其遗传性物质是所有RNA病毒中最大的,也是自然界广泛存在的一大类病毒.其粒子形状不规则,平均直径为100nm(纳米).1纳米= ,100纳米可以表示为( )米A、 B、 C、 D、5. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )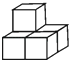 A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得C′C∥AB,则∠B′AB为( )
6. 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得C′C∥AB,则∠B′AB为( )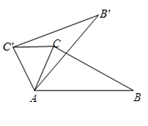 A、25° B、30° C、50° D、55°7. 2019年“周恩来读书节”活动主题是“阅读,遇见更美好的自己”.为了解同学们课外阅读情况,王老师对某学习小组10名同学5月份的读书量进行了统计,结果如下(单位:本):5,5,3,6,3,6,6,5,4,5,则这组数据的众数和中位数是()A、3,5 B、4,4 C、5,5 D、6,58. 下列命题正确是( )
A、25° B、30° C、50° D、55°7. 2019年“周恩来读书节”活动主题是“阅读,遇见更美好的自己”.为了解同学们课外阅读情况,王老师对某学习小组10名同学5月份的读书量进行了统计,结果如下(单位:本):5,5,3,6,3,6,6,5,4,5,则这组数据的众数和中位数是()A、3,5 B、4,4 C、5,5 D、6,58. 下列命题正确是( )
A、一组对边平行,另一组对边相等的四边形是平行四边形 B、有两条边对应相等的两个直角三角形全等 C、垂直于圆的半径的直线是切线 D、对角线相等的平行四边形是矩形9. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,若平行四边形ABCD的周长为28,则△ABE的周长为( ) A、28 B、24 C、21 D、1410. 三个正方形方格在扇形中的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则扇形EOF的面积为( )
A、28 B、24 C、21 D、1410. 三个正方形方格在扇形中的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则扇形EOF的面积为( )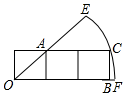 A、 π B、 π C、π D、 π11. 已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,其部分图象如图所示,下列说法中:①abc<0;②4a−2b+c<0;③若A( ,y1)、B( ,y2)、C( ,y3)是抛物线上的三点,则有 ;④若m , n( )为方程 的两个根,则 且 ,以上说法正确的有( )
A、 π B、 π C、π D、 π11. 已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,其部分图象如图所示,下列说法中:①abc<0;②4a−2b+c<0;③若A( ,y1)、B( ,y2)、C( ,y3)是抛物线上的三点,则有 ;④若m , n( )为方程 的两个根,则 且 ,以上说法正确的有( )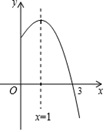 A、①②③④ B、②③④ C、①②④ D、①②③12. 如图,△ABC和△DEF都是等腰直角三角形,∠ACB=∠EFD=90°,△DEF的顶点E与△ABC的斜边AB的中点重合.将△DEF绕点E旋转,旋转过程中,线段AC与线段EF相交于点Q,射线ED与射线BC相交于点P,线段ED与AC交于点M.若AQ=4,PB=18,则MQ的长为( )
A、①②③④ B、②③④ C、①②④ D、①②③12. 如图,△ABC和△DEF都是等腰直角三角形,∠ACB=∠EFD=90°,△DEF的顶点E与△ABC的斜边AB的中点重合.将△DEF绕点E旋转,旋转过程中,线段AC与线段EF相交于点Q,射线ED与射线BC相交于点P,线段ED与AC交于点M.若AQ=4,PB=18,则MQ的长为( )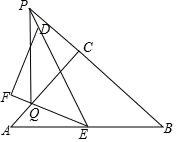 A、 B、5 C、4 D、
A、 B、5 C、4 D、二、填空题(每题3分,共12分)
-
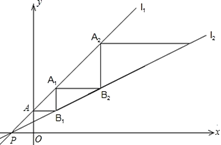
13. 因式分解: =.14. 小明要给朋友小林打电话,电话号码是七位正整数,他只记住了电话号码前四位顺序,后三位是3,6,7三位数字的某一种排列顺序,但具体顺序忘记了,那么小明第一次就拨对的概率是.15. 如图,直线l1:y=x+1与直线l2: 在x轴上相交于点P(−1,0).直线l1与y轴交于点A. 一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B1处后,改为垂直于x轴的方向运动,到达直线l1上的点A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,到达直线l1上的点A2处后,仍沿平行于x轴的方向运动,…照此规律运动,动点C依次经过点B1 , A1 , B2 , A2 , B3 , A3 , …则当动点C到达B4处时,点B4的坐标为.
 16. 已知双曲线 与直线 交于A、B两点(点A在点B的左侧).如图所示,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,则下列结论:① ;②AE=EF;③ ;④ .其中正确的是:.(填序号)
16. 已知双曲线 与直线 交于A、B两点(点A在点B的左侧).如图所示,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,则下列结论:① ;②AE=EF;③ ;④ .其中正确的是:.(填序号)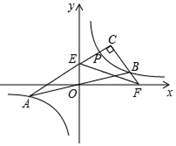
三、解答题(共52分)
-
17. 计算:18. 先化简: ,再从 的整数中选取一个合适的x的值代入求值.19. 疫情当前,为了贯彻落实教育部关于“停课不停学”的要求,某市为学生提供以下四类在线学习方式:腾讯课堂,钉钉在线课堂,校讯通以及名校同步课堂.为了解决学生需求,该市随机对部分学生发起了“你对哪类在线学习方式最感兴趣?”的调查问卷,并根据调查结果绘制出如图两幅不完整的统计图,请你根据图中提供的信息解决下列问题:
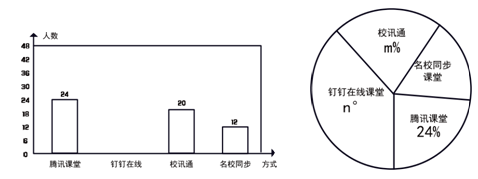 (1)、在这次调查中,一共抽取了学生;(2)、请你补全条形统计图;(3)、m=;n=;(4)、某校共有学生2000人,请你估计该校对“名校同步课堂”最感兴趣的学生有多少名?20. 如图,在平行四边形ABCD中,按下列步骤作图:
(1)、在这次调查中,一共抽取了学生;(2)、请你补全条形统计图;(3)、m=;n=;(4)、某校共有学生2000人,请你估计该校对“名校同步课堂”最感兴趣的学生有多少名?20. 如图,在平行四边形ABCD中,按下列步骤作图:①以点B为圆心,以适当长为半径作弧,交AB于点M.交BC于点N;
②再分别以点M和点N为圆心,大于 的长为半径作弧,两弧交于点G;
③作射线BG交AD于F;
④过点A作AE⊥BF交BF于点P,交BC于点E;
⑤连接EF,PD.
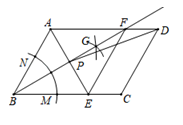 (1)、求证:四边形ABEF是菱形;(2)、若AB=8,AD=10,∠ABC=60°,求DP的长.21. 在广深高速公路改建工程中,某路段长4000米,由甲、乙两个工程队拟在30天内(含30天)合作完成,已知甲工程队每天比乙工程队多完成50米,如果甲、乙两工程队一起合作完成1500米所用时间与甲工程队单独完成1000米所用时间相同.(1)、求甲、乙两个工程队每天分别改建完成多少米?(2)、已知甲工程队每天的施工费用为0.6万元,乙工程队每天的施工费用为0.35万元,要使该工程的施工费用最低,则甲、乙两个工程队各做多少天?最低费用为多少?22. 如图1,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D.
(1)、求证:四边形ABEF是菱形;(2)、若AB=8,AD=10,∠ABC=60°,求DP的长.21. 在广深高速公路改建工程中,某路段长4000米,由甲、乙两个工程队拟在30天内(含30天)合作完成,已知甲工程队每天比乙工程队多完成50米,如果甲、乙两工程队一起合作完成1500米所用时间与甲工程队单独完成1000米所用时间相同.(1)、求甲、乙两个工程队每天分别改建完成多少米?(2)、已知甲工程队每天的施工费用为0.6万元,乙工程队每天的施工费用为0.35万元,要使该工程的施工费用最低,则甲、乙两个工程队各做多少天?最低费用为多少?22. 如图1,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D.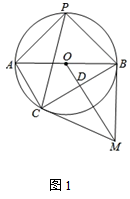 (1)、填空:OD=AC;求证:MC是⊙O的切线;(2)、若OD=9,DM=16,连接PC,求sin∠APC的值;(3)、如图2,在(2)的条件下,延长OB至N,使BN= ,在⊙O上找一点Q,使得 的值最小,请直接写出其最小值为.
(1)、填空:OD=AC;求证:MC是⊙O的切线;(2)、若OD=9,DM=16,连接PC,求sin∠APC的值;(3)、如图2,在(2)的条件下,延长OB至N,使BN= ,在⊙O上找一点Q,使得 的值最小,请直接写出其最小值为.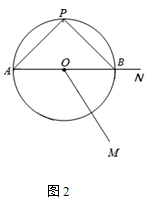 23. 如图,在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点C,抛物线 经过A,C两点,与x轴的另一交点为点B.
23. 如图,在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点C,抛物线 经过A,C两点,与x轴的另一交点为点B.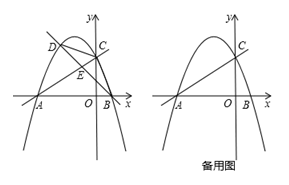 (1)、求抛物线的函数表达式;
(1)、求抛物线的函数表达式;
(2)、点D为直线AC上方抛物线上一动点;
①连接BC,CD,设直线BD交线段AC于点E, 的面积为S1 , 的面积为S2 , 求 的最大值;②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得 中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.