广东省广州市白云区2020年中考数学一模试卷
试卷更新日期:2020-07-07 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、 B、 C、9 D、2. 如图所示的几何体左视图是 ( )
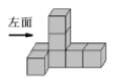 A、
A、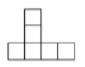 B、
B、 C、
C、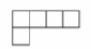 D、
D、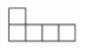 3. 一组数据: 3, 4, 5, 6, 6.这组数据的众数是 ( )A、3 B、4 C、5 D、64. 一个角是60°,则它的余角度数为 ( )A、30° B、40° C、90° D、120°5. 下列运算正确的是 ( )A、 B、 C、 D、 ( )6. 已知正多边形的每个外角是72°,则这个正多边形是 ( )A、正五边形 B、正六边形 C、正七边形 D、正八边形7. 如图,已知等边 的内切圆 半径为3,则 的长为 ( )
3. 一组数据: 3, 4, 5, 6, 6.这组数据的众数是 ( )A、3 B、4 C、5 D、64. 一个角是60°,则它的余角度数为 ( )A、30° B、40° C、90° D、120°5. 下列运算正确的是 ( )A、 B、 C、 D、 ( )6. 已知正多边形的每个外角是72°,则这个正多边形是 ( )A、正五边形 B、正六边形 C、正七边形 D、正八边形7. 如图,已知等边 的内切圆 半径为3,则 的长为 ( ) A、 B、 C、 D、8. 用一条7米长的铝材(厚度忽略不计)制成一个面积为3平方米的矩形窗框,设窗框一边长为 米, 下列方程正确的是 ( )A、 B、 C、 D、9. 下列命题中,是假命题的是 ( )A、直线 不经过第二象限 B、垂直于弦的直径平分弦 C、抛物线 与 轴有两个交点 D、对角线相等的四边形是矩形10. 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知有一种键盘密码,每个字母与所在按键的数字序号对应(见下图),如字母 与数字序号0对应,当明文中的字母对应的序号为 时,将 除以26后所得的余数作为密文中的字母对应的序号,例如明文“ ”对应密文“ ”
A、 B、 C、 D、8. 用一条7米长的铝材(厚度忽略不计)制成一个面积为3平方米的矩形窗框,设窗框一边长为 米, 下列方程正确的是 ( )A、 B、 C、 D、9. 下列命题中,是假命题的是 ( )A、直线 不经过第二象限 B、垂直于弦的直径平分弦 C、抛物线 与 轴有两个交点 D、对角线相等的四边形是矩形10. 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知有一种键盘密码,每个字母与所在按键的数字序号对应(见下图),如字母 与数字序号0对应,当明文中的字母对应的序号为 时,将 除以26后所得的余数作为密文中的字母对应的序号,例如明文“ ”对应密文“ ”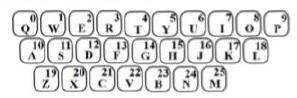
按上述规定,将密文“ ” 解密成明文后是( )
A、 B、 C、 D、二、填空题
-
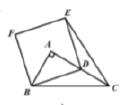
11. 比较大小:2-3(填写“>”,“<”,“=”).12. 代数式 有意义时, 应满足的条件为 .13. 四边形 内接于 ,若 ,则 的度数是°.14. 从1~5这五个整数中随机抽取两个连续整数,恰好抽中数字4的概率是 .15. 已知 为等要直角三角形,斜边 ,将 浇轴 旋转一周,可得到一个立体图形,则该立体图形的表面积是 (结果保留 ).16. 如图, 中, , ,点 在边 上运动(不与点 , 重合),以 为边作正方形 ,使点 在正方形 内,连接 ,则下列结论:
① ;②当 时, ;
③点 到直线 的距离为 ;④ 面积的最大值是 .
其中正确的结论是 . (填写所有正确结论的序号)
三、解答题
-
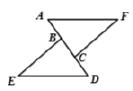
17. 解不等式: ,并在数轴上表示解集.18. 如图,点 , , , 在一条直线上, , , .
求证: .
 19. 已知 ( ).(1)、化简 ;(2)、若 的2倍比 小5,求 的值.20. 新冠肺炎疫情发生后,为支援疫情防控,某企业研发14条口罩生产线,生产普通防护口罩和普通N95口罩,现日总产量达170万只.已知每条生产线可日产普通防护口罩15万只或普通N95口罩5万只.(1)、将170万用科学记数法表示为(2)、这14条生产线中,生产普通防护口罩和普通N95口罩的生产线分别有多少条?21. 为了解“停课不停学”期间,学生对线上学习方式的偏好情况,某校随机拍取40名学生进行问卷调查,其统计结果如表:
19. 已知 ( ).(1)、化简 ;(2)、若 的2倍比 小5,求 的值.20. 新冠肺炎疫情发生后,为支援疫情防控,某企业研发14条口罩生产线,生产普通防护口罩和普通N95口罩,现日总产量达170万只.已知每条生产线可日产普通防护口罩15万只或普通N95口罩5万只.(1)、将170万用科学记数法表示为(2)、这14条生产线中,生产普通防护口罩和普通N95口罩的生产线分别有多少条?21. 为了解“停课不停学”期间,学生对线上学习方式的偏好情况,某校随机拍取40名学生进行问卷调查,其统计结果如表:最喜欢的线上学习方式(没人最多选一种)
人数
直播
10
录播
资源包
5
线上答疑
8
合计
40
(1)、 ;(2)、若将选取各种“最喜欢的线上学习方式”的人数所占比例绘制成扇形统计图,求“直播"对应扇形的圆心角度数(3)、根据调查结果估计该校10000名学生中,最喜欢“线上答疑”的学生人数;(4)、在最喜欢“资源包”的学生中,有2名男生,3名女生.现从这5名学生中随机抽取2名学生介绍学习经验,求恰好抽到1名男生和1名女生的概率.22. 如图,在 中, . (1)、利用尺规,在 边上作一点 ,使 ; (保留作图痕迹,不写作法)(2)、在(1)所作的图中,连接 ,若 ,求 的度数.23. 如图,在平面直角坐标系 中,矩形 的对角线 与 交于点 ,点 的坐标为 , 轴于点 ,反比例函数 的图象经过点 .
(1)、利用尺规,在 边上作一点 ,使 ; (保留作图痕迹,不写作法)(2)、在(1)所作的图中,连接 ,若 ,求 的度数.23. 如图,在平面直角坐标系 中,矩形 的对角线 与 交于点 ,点 的坐标为 , 轴于点 ,反比例函数 的图象经过点 .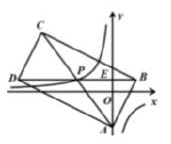 (1)、求 的值;(2)、若将矩形 向下平移 个单位,使点 落在反比例函数 的图象上,求 的值;(3)、求 的值.24. 某数学学习小组在复习线段垂直平分线性质时,提出了以下几个问题,请你帮他们解决:(1)、[数学理解]
(1)、求 的值;(2)、若将矩形 向下平移 个单位,使点 落在反比例函数 的图象上,求 的值;(3)、求 的值.24. 某数学学习小组在复习线段垂直平分线性质时,提出了以下几个问题,请你帮他们解决:(1)、[数学理解]点 是线段 垂直平分线上的一点,则 的值为;
(2)、[拓展延伸]在平面直角坐标系 中,点 , 点 在 轴上,且 , 则点 的坐标为.
(3)、经小组探究发现,如图,延长线段 到点 ,使 ,以点 为圆心, 长为半径作园,则对于 ⊙F上任一点 ,都有 ,请你证明这个结论: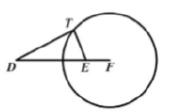 (4)、[问题解决]
(4)、[问题解决]
如图,某人乘船以25千米/时的速度沿一笔直的河 从码头 到码头 ,再立即坐车沿一笔直公路以75千米/时的速度回到住处 ,已知乘船和坐车所用的时间相等请在河 边上确定码头 的位置. (请画出示意图并简要说明理由)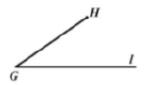 25. 已知抛物线 : ( 为常数)的顶点为 .(1)、求点 的坐标;(用含 的式子表示)(2)、在同一平面直角坐标系中,存在函数图象 ,点 在图象 上,点 在抛物线 上,对于任意的实数 ,都有点 , 关于点 对称.
25. 已知抛物线 : ( 为常数)的顶点为 .(1)、求点 的坐标;(用含 的式子表示)(2)、在同一平面直角坐标系中,存在函数图象 ,点 在图象 上,点 在抛物线 上,对于任意的实数 ,都有点 , 关于点 对称.① 当 t=1 时,求图象 对应函数的解析式;
②当 时,都有 成立,结合图象,求 的取值范围.