广东省深圳市龙岗区2019-2020学年九年级下学期数学4月月考试卷
试卷更新日期:2020-07-07 类型:月考试卷
一、单选题
-
1. 下列各数中,是无理数的是( )A、 B、 C、 D、3.14152. 以下给出的几何体中,主视图是矩形,俯视图是圆的是( )A、
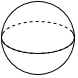 B、
B、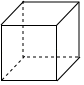 C、
C、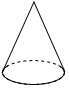 D、
D、 3. 流感病毒的半径大约为0.00000045米,它的直径用科学记数法表示为( )A、 B、 C、 D、4. 改革开放以来,我国众多科技实体在各自行业取得了举世瞩目的成就,大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表.上述四个企业的标志是轴对称图形的是( )A、
3. 流感病毒的半径大约为0.00000045米,它的直径用科学记数法表示为( )A、 B、 C、 D、4. 改革开放以来,我国众多科技实体在各自行业取得了举世瞩目的成就,大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表.上述四个企业的标志是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列计算正确的是( )A、 B、 C、 D、6. 不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )A、 B、 C、 D、7. 如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为( )
5. 下列计算正确的是( )A、 B、 C、 D、6. 不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )A、 B、 C、 D、7. 如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为( )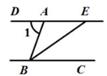 A、20° B、35° C、55° D、70°8. 若关于x的一元二次方程 有实数根,则实数k的取值范围是( )A、 B、 C、 且 D、9. 如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中错误的是()
A、20° B、35° C、55° D、70°8. 若关于x的一元二次方程 有实数根,则实数k的取值范围是( )A、 B、 C、 且 D、9. 如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中错误的是()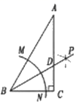 A、BP是∠ABC的平分线 B、AD=BD C、 D、CD= BD10. 下列命题是假命题的是( )A、三角形的外心到三角形的三个顶点的距离相等 B、如果等腰三角形的两边长分别是5和6,那么这个等腰三角形的周长为16 C、将一次函数y=3x-1的图象向上平移3个单位,所得直线不经过第四象限 D、若关于x的一元一次不等式组 无解,则m的取值范围是11. 如图,一艘船由 港沿北偏东65°方向航行 至 港,然后再沿北偏西40°方向航行至 港, 港在 港北偏东20°方向,则 , 两港之间的距离为( ) .
A、BP是∠ABC的平分线 B、AD=BD C、 D、CD= BD10. 下列命题是假命题的是( )A、三角形的外心到三角形的三个顶点的距离相等 B、如果等腰三角形的两边长分别是5和6,那么这个等腰三角形的周长为16 C、将一次函数y=3x-1的图象向上平移3个单位,所得直线不经过第四象限 D、若关于x的一元一次不等式组 无解,则m的取值范围是11. 如图,一艘船由 港沿北偏东65°方向航行 至 港,然后再沿北偏西40°方向航行至 港, 港在 港北偏东20°方向,则 , 两港之间的距离为( ) .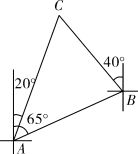 A、 B、 C、 D、12. 如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连接EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DN=DG;②△BFG∽△EDG∽△BDE;③CM垂直BD;④若MC= ,则BF=2;正确的结论有( )个
A、 B、 C、 D、12. 如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连接EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DN=DG;②△BFG∽△EDG∽△BDE;③CM垂直BD;④若MC= ,则BF=2;正确的结论有( )个 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 因式分解: .14. 若一组数据4,a,7,8,3的平均数是5,则这组数据的中位数是 .15. 如图,在△ABC中,∠BAC的平分线AD与边BC的垂直平分线ED相交于点D,过点D作DF⊥AC交AC延长线于点F,若AB=8,AC=4,则CF的长为 .
 16. 如图所示,△ABC为等边三角形,点A的坐标为(0,4),点B在x轴上,点C在反比例函数 的图象上,则点B的坐标为 .
16. 如图所示,△ABC为等边三角形,点A的坐标为(0,4),点B在x轴上,点C在反比例函数 的图象上,则点B的坐标为 .
三、解答题
-
17. 计算:18. 先化简,再求值: ,其中 , .19. “勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
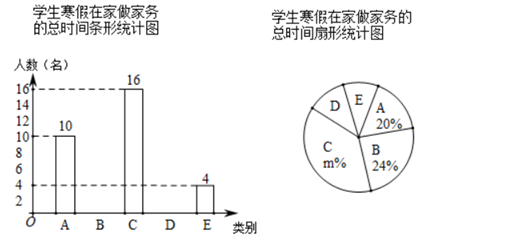
根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生;(2)、请根据以上信息直接在答题卡中补全条形统计图;(3)、扇形统计图中m的值是 , 类别D所对应的扇形圆心角的度数是度;(4)、若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.20. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F. (1)、求证:四边形AECF为矩形;(2)、连接OE,若AE=4,AD=5,求tan∠OEC的值.21. “节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)、A型自行车去年每辆售价多少元;(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多.22. 如图1所示,以点M(−1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,与⊙M相切于点H的直线EF交x轴于点E( ,0),交y轴于点F(0, ).
(1)、求证:四边形AECF为矩形;(2)、连接OE,若AE=4,AD=5,求tan∠OEC的值.21. “节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)、A型自行车去年每辆售价多少元;(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多.22. 如图1所示,以点M(−1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,与⊙M相切于点H的直线EF交x轴于点E( ,0),交y轴于点F(0, ).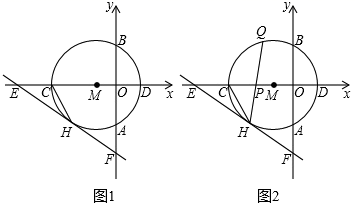 (1)、求⊙M的半径r;(2)、如图2所示,连接CH,弦HQ交x轴于点P,若cos∠QHC= ,求 的值;(3)、如图3所示,点P为⊙M上的一个动点,连接PE,PF,求PF+ PE的最小值.
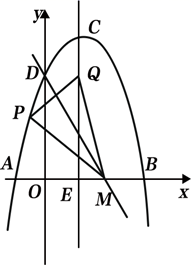
(1)、求⊙M的半径r;(2)、如图2所示,连接CH,弦HQ交x轴于点P,若cos∠QHC= ,求 的值;(3)、如图3所示,点P为⊙M上的一个动点,连接PE,PF,求PF+ PE的最小值.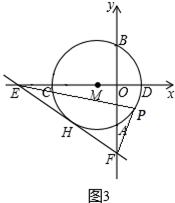 23. 如图1,抛物线 的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
23. 如图1,抛物线 的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).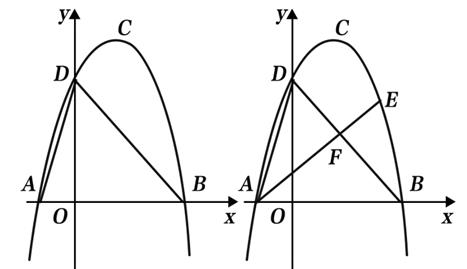 (1)、求抛物线的解析式;(2)、如图2,点E是BD上方抛物线上的一点,连接AE交DB于点F,若AF=2EF,求出点E的坐标.(3)、如图3,点M的坐标为( ,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.
(1)、求抛物线的解析式;(2)、如图2,点E是BD上方抛物线上的一点,连接AE交DB于点F,若AF=2EF,求出点E的坐标.(3)、如图3,点M的坐标为( ,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.