浙江省宁波市慈溪市2019-2020年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-07 类型：期末考试

进入出卷网下载

一、选择题(每小题3分，共30分)

1. 如图中的五个正方体大小相同，则将四个正方体A，B，C，D经平移后能得到正方体W的是（）

A、正方体A B、正方体B C、正方体C D、正方体D

查看试题解析
2. 下列四种调查中，最适宜作抽样调查的是（）

A、了解我国现代中学生喜欢的娱乐方式 B、某企业对职工进行健康检查 C、调查疫区中某社区人员感染新冠病毒的情况 D、了解本班学生视力状况

查看试题解析
3. 下列计算正确的是（）

A、(2a)³=2a³ B、a²·a³=a⁶ C、(a²)³=a⁵ D、a⁶÷a²=a⁴

查看试题解析
4. 纳米是非常小的长度单位，1纳米=10^-7厘米。经研究发现，2019新型冠状病毒(2019-n CoV)的单细胞直径范围为60纳米~140纳米，其最大直径140纳米用科学记数法表示为（）

A、1.40×10^-5厘米 B、140×10^-6厘米 C、1.40×10^-7厘米 D、0.140×10^-4厘米

查看试题解析
5. 要使分式 $\frac{x - 1}{x - 2}$ 有意义，则x的取值应满足（）

A、x=1 B、x≠1 C、x=2 D、x≠2

查看试题解析
6. 下列各组数中，不是二元一次方程2x-5y=3的解是（）

A、 ${\begin{cases} x = 1.5 \\ y = 0 \end{cases}$ B、 ${\begin{cases} x = - 1 \\ y = 1 \end{cases}$ C、 ${\begin{cases} x = 4 \\ y = 1 \end{cases}$ D、 ${\begin{cases} x = - 6 \\ y = - 3 \end{cases}$

查看试题解析
7. 不改变分式 $\frac{1.3 x - 1}{2 x - 0.7 y}$ 的值，把它的分子与分母中各项的系数化为整数，其结果正确的是（）

A、 $\frac{13 x - 1}{2 x - 7 y}$ B、 $\frac{13 x - 10}{2 x - 7 y}$ C、 $\frac{13 x - 10}{20 x - 7 y}$ D、 $\frac{13 x - 1}{20 x - 7 y}$

查看试题解析
8. 下列从左到右的变形正确的是（）

A、(-a-b)(a-b)=a²-b² B、4a²-b²=(4a+b)(4a-b) C、2x²-x-6=(2x+3)(x-2) D、4m²-6mn+9n²=(2m-3n)²

查看试题解析
9. 同一平面内五条直线l₁ ， l₂ ， l₃ ， l₄与l₅的位置关系如图所示，根据图中标示的角度，下列判断正确的是（）

A、l₁∥l₃ ， l₂∥l₃ B、l₂∥l₃ ， l₄与l₅相交 C、l₁与l₃相交，l₄∥l₅ D、I₁与l₂相交，l₁∥l₃

查看试题解析
10. 将一张边长为a的正方形纸片按图1方式放置于长方形ABCD内，再将长为b(b<a)，宽为 $\frac{b}{2}$ 的长方形纸片按图2，图3两种方式放置，长方形中未被覆盖的部分用阴影表示，设图2中阴影部分的面积为S₁ ，图3中阴影部分的面积为S₂ ，且S₂-S₁=2b，则AD-AB的值为（）

A、1 B、2 C、4 D、无法确定

查看试题解析

二、填空题(每小题4分，共24分)

11. 计算：2^-1=。

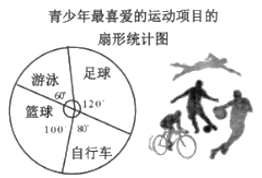
查看试题解析
12. 计算：(4a³-6a) ÷(2a)=。

查看试题解析
13. 在某校对若干名青少年进行最喜爱的运动项目的抽样调查中，得到如下统计图。如果最喜爱足球的人数比最喜爱骑自行车的人数多30人，那么参加这次调查的总人数是人。

查看试题解析
14. 如图，把一块含45°角的三角尺的直角顶点放在直尺的一边上。若∠1=32°，则∠2的度数是。

查看试题解析
15. 已知实数a，b满足ab-3=0，a+b=4，则a-b= 。

查看试题解析
16. 小慧带着妈妈给的现金去蛋糕店买蛋糕。他若买5个巧克力蛋糕和3个桂圆蛋糕，则妈妈给的钱不够，还缺16元；若买3个巧克力蛋糕和5个桂圆蛋糕，则妈妈给的钱还有剩余，还多10元。若他只买8个桂圆蛋糕，则剩余的钱为元。

查看试题解析

三、解答题(第17、18题各6分，第19、20、21、22题各8分，第23题10分，第24题12分，共66分)

17. 计算：

(1)、2a⁵+(-a²)³÷a

(2)、(m-2n)²+(m-2n)(m+2n)

查看试题解析
18. 因式分解：

(1)、3x²-6xy+3y²

(2)、(a-b)²-a+b

查看试题解析
19. 先化简，再求值： $\frac{4}{a^{2} - 4} - \frac{1}{a - 2}$ ，其中a=- $\frac{3}{2}$ 。

查看试题解析
20. 解方程(组)：

(1)、 $\frac{x}{x - 2} = 1 + \frac{x + 1}{x - 2}$

(2)、 ${\begin{cases} 2 x - 5 y = 27 \\ 3 x + y = - 2 \end{cases}$

查看试题解析
21. 受新冠病毒影响，2020年春浙江省中小学延期开学，复学后，某校为了解学生对防疫知识的掌握情况，学校组织全体学生进行防疫知识竞赛。从中抽取了8%的学生的竞赛成绩(满分100，成绩为整数)作为样本，整理后绘制成如图所示的频数直方图。请结合直方图解答下列问题：

(1)、求此次抽取的样本容量及全校学生人数。

(2)、求竞赛成绩在84.5~89.5这一组的频率。

(3)、如果竞赛成绩在90分以上(含90分)的同学可以获得奖励，请估计全校学生中约有多少人获得奖励。

查看试题解析
22. 如图，已知∠1=∠BDE，∠2+∠FED=180°。

(1)、证明：AD∥EF。

(2)、若EF⊥BF于点F，且∠FED=140°。求∠BAC的度数。

查看试题解析
23. 为创建省文明卫生城市，某街道将一公园进行绿化改造．计划种植甲、乙两种花木，甲种花木每棵进价800元，乙种花木每棵进价3000元，共需107万元；每种植一棵甲种花木需人工费30元，每种植一棵乙种花木需人工费80元，共需人工费32000元。

(1)、求计划种植甲、乙两种花木各多少棵？

(2)、如果承包植树的老板安排28人同时种植这两种花木，每人每天能种植甲种花木20棵或乙种花木5棵，应分别安排多少人种植甲种花木和乙种花木，才能确保同时完成各自的任务？

查看试题解析
24. 阅读下列材料：
【材料1】我们知道，假分数可以化为整数与真分数的和的形式，例如： $\frac{3}{2}$ =1+ $\frac{1}{2}$ 。在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为假分式；当分子的次数小于分母的次数时，我们称之为真分式，如 $\frac{x + 1}{x - 1}$ ， $\frac{x^{2}}{x - 2}$ ，…这样的分式是假分式；如 $\frac{2 x - 1}{x^{2} + x}$ 与 $\frac{5}{3 x^{2} + 2}$ …这样的分式是真分式。类似的，假分式也可以化为整式与真分式的和(差)的形式。

例如：将分式 $\frac{x^{2} + 2 x - 5}{x + 3}$ 化成一个整式与一个真分式的和(差)的形式。

方法1： $\frac{x^{2} + 2 x - 5}{x + 3}$ = $\frac{(x^{2} + 3 x) - x - 5}{x + 3}$ = $\frac{x (x + 3) - (x + 3) - 2}{x + 3}$ =x-1- $\frac{2}{x + 3}$

方法2：由分母为x+3，可设x²+2x-5=(x+3)(x+a)+b(a，b为待确定的系数)

∵(x+3)(x+a)+b=x²+ax+3x+3a+b=x²+(a+3)x+(3a+b)

∴x²+2x-5=x²+(a+3)x+(3a+b)

对于任意x，上述等式均成立，

∴ ${\begin{cases} a + 3 = 2 \\ 3 a + b = - 5 \end{cases}$ ，解得 ${\begin{cases} a = - 1 \\ b = - 2 \end{cases}$

∴x²+2x-5=(x+3)(x-1)-2

∴ $\frac{x^{2} + 2 x - 5}{x + 3}$ = $\frac{(x + 3) (x - 1) - 2}{x + 3}$ = $\frac{(x + 3) (x - 1)}{x + 3} - \frac{2}{x + 3}$ =x-1- $\frac{2}{x + 3}$

这样，分式 $\frac{x^{2} + 2 x - 5}{x + 3}$ 就被化成一个整式与一个真分式的和(差)的形式。

【材料2】对于式子2+ $\frac{3}{1 + x^{2}}$ ，由x²≥0知1+x²的最小值为1，所以 $\frac{3}{1 + x^{2}}$ 的最大值为3，

所以2+ $\frac{3}{1 + x^{2}}$ 的最大值为5。

请根据上述材料，解答下列问题：

(1)、分式 $\frac{2}{x + 2}$ 是分式(填“真”或“假”)。

(2)、把下列假分式化成一个整式与一个真分式的和(差)的形式：
① $\frac{2 x + 3}{x}$ =+。

② $\frac{x^{2} - 3 x + 5}{x - 3}$ =+。

(3)、把分式 $\frac{x^{2} + 2 x - 13}{x - 3}$ 化成一个整式与一个真分式的和(差)的形式，并求x取何整数时，这个分式的值为整数。

(4)、当x的值变化时，求分式 $\frac{2 x^{2} - 4 x + 8}{x^{2} - 2 x + 2}$ 的最大值。

查看试题解析