浙江省湖州市长兴县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-07-07 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分) 下面每小题给出的四个选项中,只有一个是正确的,请选出各题中一个最符合题意的选项不选、多选、错选的均不给分。
-
1. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、2. 在下列图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在下列方程中,不属于一元二次方程的是( )A、 =x B、7x2=0 C、0.3x2+0.2x=4 D、x(1-2x2)=2x24. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,点E,F分别是AC,AB的中点,则线段EF的长为( )
3. 在下列方程中,不属于一元二次方程的是( )A、 =x B、7x2=0 C、0.3x2+0.2x=4 D、x(1-2x2)=2x24. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,点E,F分别是AC,AB的中点,则线段EF的长为( ) A、3 B、4 C、5 D、65. 如图,平行四边形ABCD的对角线交于点E,已知AB=5cm,△ABE的周长比△BEC的周长小3cm,则AD的长度为( )
A、3 B、4 C、5 D、65. 如图,平行四边形ABCD的对角线交于点E,已知AB=5cm,△ABE的周长比△BEC的周长小3cm,则AD的长度为( ) A、8cm B、5cm C、3cm D、2cm6. 菱形具有而矩形不一定有的性质是( )A、对角线互相平分 B、四条边都相等 C、对角相等 D、邻角互补7. 已知5个数a1 , a2 , a3 , a4 , a5的平均数是a,则数据0,a1 , a2 , a3 , a4 , a5的平均数为( )A、a B、a+1 C、 a D、 a8. 用反证法证明“在三角形中,至少有一个内角大于或等于60°”时,应先假设( )A、在三角形中,三个内角都大于60° B、在三角形中,三个内角都小于60° C、在三角形中,至少有一个内角大于60° D、在三角形中,至少有一个内角小于60°9. 某校坚持对学生进行近视眼的防治,近视学生人数逐年减少。据统计,今年的近视学生人数是前年近视学生人数的75%,那么这两年平均每年近视学生人数降低的百分率是多少?设平均每年降低的百分率为x,根据题意列方程得( )A、1-x2=75% B、(1+x)2=75% C、1-2x=75% D、(1-x)2=75%10. 我国古代数学家研究过一元二次方程(正根)的几何解法,以方程x2+5x-14=0,即x(x+5)=14为例说明。《方图注》中记载的方法是:构造图(如左下图)中大正方形的面积是(x+x+5)2 , 同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+5²,因此x=2。则在下面构图中,能正确说明方程x2-3x-10=0的构图是( )
A、8cm B、5cm C、3cm D、2cm6. 菱形具有而矩形不一定有的性质是( )A、对角线互相平分 B、四条边都相等 C、对角相等 D、邻角互补7. 已知5个数a1 , a2 , a3 , a4 , a5的平均数是a,则数据0,a1 , a2 , a3 , a4 , a5的平均数为( )A、a B、a+1 C、 a D、 a8. 用反证法证明“在三角形中,至少有一个内角大于或等于60°”时,应先假设( )A、在三角形中,三个内角都大于60° B、在三角形中,三个内角都小于60° C、在三角形中,至少有一个内角大于60° D、在三角形中,至少有一个内角小于60°9. 某校坚持对学生进行近视眼的防治,近视学生人数逐年减少。据统计,今年的近视学生人数是前年近视学生人数的75%,那么这两年平均每年近视学生人数降低的百分率是多少?设平均每年降低的百分率为x,根据题意列方程得( )A、1-x2=75% B、(1+x)2=75% C、1-2x=75% D、(1-x)2=75%10. 我国古代数学家研究过一元二次方程(正根)的几何解法,以方程x2+5x-14=0,即x(x+5)=14为例说明。《方图注》中记载的方法是:构造图(如左下图)中大正方形的面积是(x+x+5)2 , 同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+5²,因此x=2。则在下面构图中,能正确说明方程x2-3x-10=0的构图是( )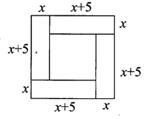 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(本题有6小题,每小题4分,共24分)
-
11. 当x=4时,二次根式 的值是。12. 已知样本数据为3,4,2,1,5,则标准差是 。13. 一个内角和为720°的多边形的边数是。14. 一个一元二次方程的二次项系数为1,其中一个根是-3,另一个根是2,则这个方程是。15. 如图,以正方形ABCD的一边AD为边向外作等边△ADE,则∠BED的度数是。
 16. 如图,过原点的直线与反比例函数y= (k>0)的图象交于点A,点B,已知点C的坐标是(6,0),且AC⊥BC,连结AC,交反比例函数图象于点D,若AD=CD,则k的值为。
16. 如图,过原点的直线与反比例函数y= (k>0)的图象交于点A,点B,已知点C的坐标是(6,0),且AC⊥BC,连结AC,交反比例函数图象于点D,若AD=CD,则k的值为。
三、解答题(本题共有8小题,共66分)
-
17. 计算:18. 解方程:(x-1)2=2x+119. 已知反比例函数y= (k≠0),当x=-3时,y= 。(1)、求y关于x的函数表达式。(2)、当y=-4时,求自变量x的值。20. 如图,在平行四边形ABCD中,E,F为AB边上的两点,且AE=BF,DF=CE。

求证:
(1)、△ADF≌△BCE。(2)、平行四边形ABCD是矩形。21. 在学校组织的跳绳比赛中,每班参加的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为10分,9分,8分,7分,现将801班和802班的成绩整理并绘制成如下的统计图。
请根据以上提供的信息解答下列问题:
(1)、此次比赛中,801班成绩在C级以上(包括C级)的人数为。(2)、将下列表格补充完整。平均分(分)
中位数(分)
众数(分)
801班
8.76
9
802班
8.76
10
(3)、根据信息分析,你认为两个班哪个班成绩好一些,请说明理由。22. 如图,已知一次函数y=3x的图象与反比例函数y= 的图象交于点A(a,3)。 (1)、求a和k的值。(2)、若点P(m,n)在反比例函数图象上,且点P到x轴的距离小于3,请根据图象直接写出m的取值范围。23. 某商场销售一批衬衫,平均每天可以售出20件,每件盈利40元。为回馈顾客,商场决定采取适当的降价措施。经调查发现,每件衬衫降价1元,商场平均每天可多售出2件。(1)、若每件衬衫降价5元,商场可售出多少件?(2)、若商场每天的盈利要达到1200元,每件衬衫应降价多少元?24. 小明对教材“课题学习”中的“用一张正方形折出一个正八边形”的问题进行了认真的探索。已知AC是正方形ABCD的对角线,把∠BAC对折,使点B落在AC上,记为点E,再沿CE的中垂线折叠,得到折痕PQ,如图1。类似地,折出其余三条折痕GH,IJ,KO,得到八边形GHIJKOPQ,如图2。
(1)、求a和k的值。(2)、若点P(m,n)在反比例函数图象上,且点P到x轴的距离小于3,请根据图象直接写出m的取值范围。23. 某商场销售一批衬衫,平均每天可以售出20件,每件盈利40元。为回馈顾客,商场决定采取适当的降价措施。经调查发现,每件衬衫降价1元,商场平均每天可多售出2件。(1)、若每件衬衫降价5元,商场可售出多少件?(2)、若商场每天的盈利要达到1200元,每件衬衫应降价多少元?24. 小明对教材“课题学习”中的“用一张正方形折出一个正八边形”的问题进行了认真的探索。已知AC是正方形ABCD的对角线,把∠BAC对折,使点B落在AC上,记为点E,再沿CE的中垂线折叠,得到折痕PQ,如图1。类似地,折出其余三条折痕GH,IJ,KO,得到八边形GHIJKOPQ,如图2。 (1)、求证:△CPQ是等腰直角三角形。(2)、若AB=a,求PQ的长。(用含a的代数式表示)(3)、我们把八条边长相等,八个内角都相等的八边形叫做正八边形。请说明八边形GHLJKOPQ是正八边形的理由。
(1)、求证:△CPQ是等腰直角三角形。(2)、若AB=a,求PQ的长。(用含a的代数式表示)(3)、我们把八条边长相等,八个内角都相等的八边形叫做正八边形。请说明八边形GHLJKOPQ是正八边形的理由。