湖北省武汉市青山区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-07 类型：期末考试

进入出卷网下载

一、选择题

1. 4的算术平方根是（　　）

A、2 B、-2 C、±2 D、16

查看试题解析
2. 一个不等式组中两个不等式的解集如图所示，则这个不等式组的解集是（）

A、 $0 \leq x < 1$ B、 $0 < x < 1$ C、 $0 \leq x \leq 1$ D、 $0 < x \leq 1$

查看试题解析
3. 下列调查中，最适宜采用全面（普查）的是（）

A、了解武汉市市民对中美贸易争端的知晓情况 B、了解一批导弹的杀伤半径 C、对乘坐飞机的旅客是否携带违禁物品的调查 D、对长江中下游流域水质情况的调查

查看试题解析
4. 方程组 ${\begin{array}{l} x - y = 1 \\ 2 x + y = 5 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 1 \\ y = - 2 \end{array}$ B、 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$

查看试题解析
5. 已知 $a < b$ ，下列不等式中，变形正确的是 $($ $)$

A、 $a - 3 > b - 3$ B、 $3 a - 1 > 3 b - 1$ C、 $- 3 a > - 3 b$ D、 $\frac{a}{3} > \frac{b}{3}$

查看试题解析
6.
如图，直线a∥b ，直线l分别与直线a ， b相交于点P ， Q ， PA垂直于l于点P ．若∠1=64°，则∠2的度数为（）

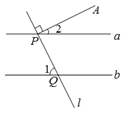A、26° B、30° C、36° D、64°

查看试题解析
7. 在平面直角坐标系中，将点 $A (m, m + 9)$ 向右平移4个单位长度，再向下平移2个单位长度，得到点B，若点B在第二象限，则m的取值范围是（）

A、 $- 11 < m < - 4$ B、 $- 7 < m < - 4$ C、 $m < - 7$ D、 $m > - 4$

查看试题解析
8. 我国古代数学著作《算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托.折回索子来量竿，却比竿子短一托.”其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺.设绳索长x尺，竿长y尺，则符合题意的方程组是（）

A、 ${\begin{array}{l} x = y + 5 \\ \frac{1}{2} x = y - 5 \end{array}$ B、 ${\begin{array}{l} x = y + 5 \\ \frac{1}{2} x - 5 = y \end{array}$ C、 ${\begin{array}{l} x + 5 = y \\ 2 x = y - 5 \end{array}$ D、 ${\begin{array}{l} x = y - 5 \\ \frac{1}{2} x = y + 5 \end{array}$

查看试题解析
9. 数学活动课上，张老师为更好促进学生开展小组合作学习，将全班40名学生分成4人或6人学习小组，则分组方案有（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
10. 关于 $x$ 的不等式组 ${\begin{array}{l} x - 2 a \leq 0 \\ 2 x + 3 a > 0 \end{array}$ 的解集中至少有7个整数解，则整数a的最小值是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 2的相反数是．

查看试题解析
12. 某校学生来自甲，乙，丙三个地区，其人数比为2：3：7，如图所示的扇形图表示上述分布情况，其中甲所对应扇形的圆心角的度数为.

查看试题解析
13. 如图，不添加辅助线，请写出一个能判定 $A B ∥ C D$ 的一个条件是.

查看试题解析
14. 在实数范围内定义一种新运算“ $\oplus$ ”，其运算规则为： $a \oplus b = 2 a + 3 b$ .如： $1 \oplus 5 = 2 \times 1 + 3 \times 5 = 17$ ，则不等式 $x \oplus 4 < 2$ 的解集为.

查看试题解析
15. 如图，用8块相同的长方形地砖拼成一个大长方形，则每个长方形地砖的面积为 $c m^{2}$ .

查看试题解析
16. 如图，三角形 $A B C$ 中，A，B，C三点的坐标分别为 $(4 ， 3)$ ， $(3 ， 1)$ ， $(1 ， 2)$ ，点 $P (m ， 0)$ 是 $x$ 轴上一动点，若 $S_{△ A B P} > S_{△ A B C}$ ，则m的取值范围是.

查看试题解析
17. 解方程组：

(1)、 ${\begin{array}{l} x - y = 1 \\ 2 x + y = 8 \end{array}$ ；

(2)、 ${\begin{array}{l} 3 x + 4 y = 16 \\ 5 x - 6 y = 33 \end{array}$ .

查看试题解析
18. 解不等式，并在数轴上表示解集： $\frac{x - 2}{3} \geq \frac{3 x - 1}{2} - 2$ .

查看试题解析
19. 某商店以每辆250元的进价购入200辆自行车，并以每辆275元的价格销售.两个月后自行车的销售款已超过这批自行车的进货款，这时至少已售出多少辆自行车？

查看试题解析

20. “品中华诗词，寻文化自信”.某校组织全校1000名学生举办了第二届“中华诗词大赛”的初赛，从中抽取部分学生的成绩统计后，绘制了如下不完整的频数分布统计表与频数分布直方图.

频数分布统计表

组别	成绩 $x$ （分）	人数	百分比
$A$	$60 \leq x < 70$	8	20%
$B$	$70 \leq x < 80$	16	$m %$
$C$	$80 \leq x < 90$	$a$	30%
$D$	$90 \leq x \leq 100$	4	10%

频数分布直方图

请观察图表，解答下列问题：

(1)、表中

a =

，

m =

；

(2)、补全频数分布直方图；

(3)、如果成绩达到90及90分以上者为优秀，可推荐参加决赛，那么请你估计该校进入决赛的学生大约有多少人？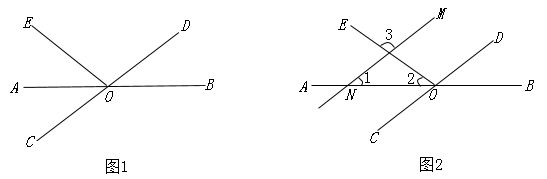

查看试题解析

21. 已知，直线 $A B$ ， $C D$ 相交于点 $O$ .

(1)、如图1，若 $O A$ 平分 $∠ E O C$ ， $∠ E O C ： ∠ E O D = 2 ： 3$ ，求 $∠ B O D$ 的度数；

(2)、如图2， $M N ∥ C D$ 交 $O E$ 于点 $F$ ，交 $O A$ 于点 $N$ ，且 $∠ 1 + ∠ 2 = \frac{7}{8} ∠ 3$ ， $2 ∠ 1 + \frac{1}{2} ∠ 2 = ∠ 3$ ，求 $∠ B O D$ 的度数.

查看试题解析
22. 为响应党中央“下好一盘棋，共护一江水”的号召，某治污公司决定购买甲、乙两种型号的污水处理设备共10台.经调查发现：购买一台甲型设备比购买一台乙型设备多2万元，购买2台甲型设备比购买3台乙型设备少6万元，且一台甲型设备每月可处理污水240吨，一台乙型设备每月可处理污水200吨.

(1)、请你计算每台甲型设备和每台乙型设备的价格各是多少万元？

(2)、若治污公司购买污水处理设备的资金不超过109万元，月处理污水量不低于2080吨.
①求该治污公司有几种购买方案；

②如果为了节约资金，请为该公司设计一种最省钱的购买方案.

查看试题解析
23. 已知， $∠ B A M$ 与 $∠ A B N$ 两角的角平分线交于点P，D是射线 $B P$ 上一个动点，过点D的直线分别交射线 $A M$ ， $B N$ ， $A P$ 于点E，F，C.

(1)、如图1，若 $∠ B A M = 140 °$ ， $∠ A B N = 68 °$ ， $A B ∥ E F$ ，求 $∠ B P C$ 的度数；

(2)、如图2，若 $A C ⊥ B D$ ，请探索 $∠ A E F$ 与 $∠ B F E$ 的数量关系，并证明你的结论；

(3)、在点 $D$ 运动的过程中，请直接写出 $∠ A E F$ ， $∠ B F E$ 与 $∠ B P C$ 这三个角之间满足的数量关系：.

查看试题解析
24. 已知，点A，点D分别在y轴正半轴和负半轴上， $A B ∥ D E$ .

(1)、如图1，若 $m = \sqrt{4 - m} + 4$ ， $∠ B A D = m ∠ O E D$ ，求 $∠ C A D$ 的度数；

(2)、在 $∠ B A O$ 和 $∠ D E O$ 内作射线 $A M$ ， $E N$ ，分别与过 $O$ 点的直线交于第一象限内的点 $M$ 和第三象限内的点 $N$ .
①如图2，若 $A M$ ， $E N$ 恰好分别平分 $∠ B A O$ 和 $∠ D E O$ ，求 $∠ A M N - ∠ E N M$ 的值；

②若 $∠ M A O = \frac{1}{n} ∠ B A M$ ， $∠ N E O = \frac{1}{n} ∠ N E D$ ，当 $40 ° < ∠ A M N - ∠ E N M < 60 °$ ，求N的取值范围。

查看试题解析