湖北省武汉市江汉区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-07 类型：期末考试

进入出卷网下载

一、选择题

1. 已知 $m = \sqrt{10}$ ，估计m的值所在的范围是（）

A、1＜m＜2 B、2＜m＜3 C、3＜m＜4 D、4＜m＜5

查看试题解析
2. 下列调查中，适合采用全面调查的是（）

A、调查长江的水质情况 B、调查全市中学生每天的就寝时间 C、调查一枚火箭所有零件的合格情况 D、调查某批次汽车的抗撞击能力

查看试题解析
3. 如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是（）

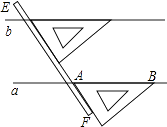A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，内错角相等

查看试题解析
4. 已知(x +1)²= 16 ，则 x 的值是（）

A、3 B、7 C、3 或-5 D、7 或-8

查看试题解析
5. 若 ${\begin{array}{l} x = 0 \\ y = 1 \end{array}$ 和 ${\begin{array}{l} x = - 1 \\ y = - 1 \end{array}$ 都是方程y＝kx＋b的解，则k、b的值分别是（）

A、k＝2，b＝－1 B、k＝2，b＝1 C、k＝ $\frac{1}{2}$ ，b＝－1 D、k＝ $\frac{1}{2}$ ，b＝1

查看试题解析
6. 如图，在四边形ABCD中，∠A＝∠B＝2∠C＝90°，则∠D的度数为（）

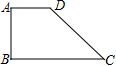A、120° B、125° C、130° D、135°

查看试题解析
7. 下列不等式变形，成立的是（）

A、若m＜n，则m－2＜n－2 B、若m＜n，则2－m＜2－n C、若m＜n，则－2m＜－2n D、若m＜n，则 $- \frac{m}{2} < - \frac{n}{2}$

查看试题解析
8. 《九章算术》是我国古代数学的经典书，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等；交易其一，金轻十三两.问金、银一枚各重几何？”意思是甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等.两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）.问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，则可列方程组为（）

A、 ${\begin{array}{l} 11 x = 9 y \\ (10 y + x) - (8 x + y) = 13 \end{array}$ B、 ${\begin{array}{l} 9 x = 11 y \\ (8 x + y) - (10 y + x) = 13 \end{array}$ C、 ${\begin{array}{l} 9 x = 11 y \\ (10 y + x) - (8 x + y) = 13 \end{array}$ D、 ${\begin{array}{l} 11 x = 9 y \\ (8 x + y) - (10 y + x) = 13 \end{array}$

查看试题解析
9. 某同学为了估算瓶子中有多少颗豆子，首先从瓶中取出60颗并做上记号，接着将所有做好记号的豆子放回瓶中充分摇匀.当再从瓶中取出100颗豆子时，发现其中有12颗豆子标有记号，根据实验估计该瓶装有豆子大约（）

A、800颗 B、500颗 C、300颗 D、150颗

查看试题解析
10. 如图，射线OA是第三象限角平分线，若点B(k－3，1－2k)在第三象限内且在射线OA的下方，则k的取值范围是（）

A、 $k < \frac{1}{2}$ B、 $\frac{1}{2} < k < 3$ C、 $\frac{1}{2} < k < \frac{4}{3}$ D、 $\frac{4}{3} < k < 3$

查看试题解析

二、填空题

11. 点A是x轴上位于原点左侧的一点，且与点B(1，0)的距离为3个单位长度，则点A的坐标为.

查看试题解析
12. 整理某个样本，其中最大值是24，最小值是2，取组距为3，则该样本可以分为组.

查看试题解析
13. 已知点P(t＋1，2－t)在y轴上，则点P的坐标为.

查看试题解析
14. 若 $\frac{x}{2} = \frac{y}{3} = \frac{z}{4}$ ，则x－2y＋z＝.

查看试题解析
15. 某种葡萄的进价是2.7元/千克，销售过程中估计有10%的正常损耗，商家为了避免亏本，至少应将售价定为元/千克

查看试题解析
16. 如图，长方形ABCD中，AD＝5，AB＝3.已知点M是BC边上一点，且AM＝4，则点D到AM的距离为.

查看试题解析

三、解答题

17. 解答下列各题：

(1)、计算： $\sqrt{16} - \sqrt[3]{8} - | \sqrt{3} - 2 |$

(2)、解方程组： ${\begin{array}{l} 3 x - 2 y = 1 \\ 4 x + 3 y = 7 \end{array}$

查看试题解析
18. 解下列不等式或不等式组：

(1)、 $\frac{x - 3}{2} > \frac{2 x - 5}{3} + 1$

(2)、 ${\begin{array}{l} 3 (x - 1) \geq x + 3 \\ 3 x + 1 > 4 x - 3 \end{array}$

查看试题解析
19. 把一些练习本分给几名同学，如果每人分6本，那么多出4本；如果每人分7本，那么其中有一人分得到练习本，但所得不足3本，求这些练习本有多少本？共有多少名学生？

查看试题解析

20. 某学校随机选取40名学生进行军运会知识考查，对考查成绩进行统计（成绩均为整数），并依据统计数据绘制了如下统计图表.解答下列问题：

组别	分数段/分	频数	频率
1	50.5~60.5	2	a
2	60.5~70.5	6	0.15
3	70.5~80.5	b	c
4	80.5~90.5	12	0.30
5	90.5~100.5	6	0.15
合计		40	1.00

(1)、表中a＝；b＝；c＝；

(2)、请补全频数分布直方图；

(3)、已知该学校共有学生1280人，若考查成绩80分以上（不含80分）为优秀，试估计该学校学生军运会知识考查成绩达到优秀的人数.

查看试题解析

21. 如图，点B、C在线段AD的异侧，点E、F分别是线段AB、CD上的点.已知∠AEG＝∠AGE，∠DCG＝∠DGC.

(1)、求证：AB∥CD

(2)、若∠AGE＋∠AHF＝180°，且∠BFC－30°＝2∠C，求∠B的度数

查看试题解析

四、填空题（二）

22. 4条直线相交于一点时，共有对邻补角.

查看试题解析
23. 如图，AB∥CD，BE∥DF，∠DBE和∠CDF的角平分线交于点G.当∠BGD＝65°时，∠BDC＝度.

查看试题解析
24. 已知关于x的不等式组 ${\begin{array}{l} x + m > 1 \\ 4 (x - \frac{1}{4}) \leq 3 x + 2 \end{array}$ 有2019个整数解，则m的取值范围是.

查看试题解析
25. 已知一个两位数，将其个位上的数和十位上的数对调后组成一个新的两位数.若原两位数与8的和不大于新两位数的一半，则满足条件的两位数有个.

查看试题解析

五、解答题

26. 某风景区票价如下表所示：

人数/人

1～40

41～80

80以上

价格/元/人

150

130

120

有甲、乙两个旅行团队共计100人，计划到该景点游玩.已知乙队多于甲队人数的 $\frac{1}{4}$ ，但不超过甲队人数的 $\frac{2}{3}$ ，且甲、乙两队分别购票共需13600元

(1)、试通过计算判断，甲、乙两队购票的单价分别是多少？

(2)、求甲、乙两队分别有多少人？

(3)、暑期将至，该风景区计划对门票价格做如下调整：人数不超过40人时，门票价格不变；人数超过40人但不超过80人时，每张门票降价a元；人数超过80人时，每张门票降价2a元，其中a＞0.若甲、乙两队联合购票比分别购票最多可节约2250元，直接写出a的取值范围

查看试题解析
27. 在平面直角坐标中，A (0，5)、B (4，0)、C (2，5)，四边形AOBC经过平移后得到四边形A′O′B′C′.

(1)、如图1，若A′(－3，5)，四边形AOBC内部一点M(a＋b－2，6a－7)经过平移后得到点N(a＋2b－7，4b－6)，求M点的坐标

(2)、如图2，若四边形AOBC向右平移m个单位长度（m＞0）.当m为何值时，重叠部分的面积比四边形BB′C′C的面积大

(3)、如图3，若四边形AOBC向上平移2个单位长度，直接写出图中阴影部分的面积.

查看试题解析
28. △ABC在平面直角坐标系内如图1摆放，A、C两点的横坐标都是5，BC∥x轴.已知B点坐标为(－3，m)，AB交y轴于点D，且AC＝BC.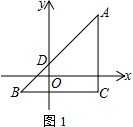

(1)、填空：BC＝；△ABC的面积为；用m表示点A的坐标为.

(2)、射线BO交直线AC于点Q，若△ABQ的面积为16，试求m的值

(3)、如图2，点D在y轴负半轴上，∠BAC的三等分线AP与∠BOD的角平分线OP交于点P，其中∠BAC＝3∠BAP＝45°.若∠P＞2∠B，试求∠BOD的取值范围.

查看试题解析

人数/人	1～40	41～80	80以上
价格/元/人	150	130	120