河南省驻马店市上蔡县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-07 类型:期末考试
一、选择题
-
1. 下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 方程2x-1=3x+2的解为( )A、x=1 B、x=-1 C、x=3 D、x=-33. 二元一次方程组 的解是( )A、 B、 C、 D、4. 不等式 的解集在数轴上表示为( )A、
2. 方程2x-1=3x+2的解为( )A、x=1 B、x=-1 C、x=3 D、x=-33. 二元一次方程组 的解是( )A、 B、 C、 D、4. 不等式 的解集在数轴上表示为( )A、 B、
B、 C、
C、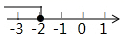 D、
D、 5. 已知一个三角形的两边长分别为4,7,则第三边的长可以为( )A、2 B、3 C、8 D、126. 如图,将周长为4的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )
5. 已知一个三角形的两边长分别为4,7,则第三边的长可以为( )A、2 B、3 C、8 D、126. 如图,将周长为4的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )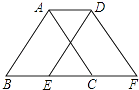 A、5 B、6 C、7 D、87. 在现实生活中,铺地最常见的是用正方形地板砖,某小区广场准备用多种地板砖组合铺设,则能够选择的组合是
A、5 B、6 C、7 D、87. 在现实生活中,铺地最常见的是用正方形地板砖,某小区广场准备用多种地板砖组合铺设,则能够选择的组合是 A、正三角形,正方形 B、正方形,正六边形 C、正五边形,正六边形 D、正六边形,正八边形8. 已知不等式 的负整数解恰好是-3,-2,-1.那么a满足条件( )A、 B、 C、 D、9. 在一个 边形的 个外角中,钝角最多有( )A、2个 B、3个 C、4个 D、5个10. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )
A、正三角形,正方形 B、正方形,正六边形 C、正五边形,正六边形 D、正六边形,正八边形8. 已知不等式 的负整数解恰好是-3,-2,-1.那么a满足条件( )A、 B、 C、 D、9. 在一个 边形的 个外角中,钝角最多有( )A、2个 B、3个 C、4个 D、5个10. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )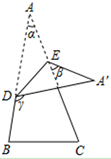 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如果 是方程 的解,那么a的值是.12. 若一个正多边形的每一个外角都是30°,则这个正多边形的边数为 .13. 若关于x,y的方程组 的解满足 ,则m的值为.14. 不等式组 有三个整数解,则m的取值范围是.15. 如图,在 中,沿 折叠,点C落在点B处,已知 的周长是15, ,则 的周长为.
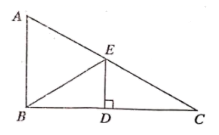
三、解答题
-
16. 按要求解方程(组)(1)、(2)、17. 不等式(组)(1)、解不等式: ,并把解集表示在数轴上.(2)、解不等式组: ,并写出整数解.18. 已知方程组 的解满足x为非正数,y为负数.(1)、求m的取值范围;(2)、在(1)的条件下,若不等式 的解为 .请直接写出整数m的值为.19. 如图所示的正方形方格(每个小正方形的边长为1个单位). 的三个顶点均在小方格的顶点上.
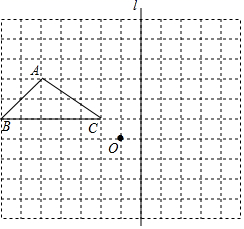 (1)、①画出 关于O点的中心对称图形 ;
(1)、①画出 关于O点的中心对称图形 ;②画出将 沿直线l向上平移5个单位得到的 ;
(2)、要使 与 重合,则 绕点 顺时针方向至少旋转的度数为.20. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数。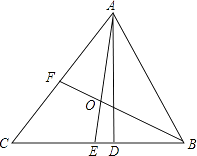 21. 初一五班共有学生42人,其中男生人数比女生人数的2倍少3人.(1)、该班男生和女生各有多少人?(2)、学校决定派该班30名学生勤工俭学,练习制作乐高零件,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少需要派多少名男学生?22. 某校计划购买篮球和排球两种球若干.已知购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同.(1)、求篮球和排球的单价;(2)、该校计划购买篮球和排球共30个.某商店有两种优惠活动(两种优惠活动不能同时参加),活动一:一律打九折,活动二:购物不超过600元时不优惠,超过600元时,超过600元的部分打八折.请根据以上信息,说明选择哪一种活动购买篮球和排球更实惠.23. 如图,已知 ,现将一直角三角形 放入图中,其中 , 交 于点 , 交 于点F.
21. 初一五班共有学生42人,其中男生人数比女生人数的2倍少3人.(1)、该班男生和女生各有多少人?(2)、学校决定派该班30名学生勤工俭学,练习制作乐高零件,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少需要派多少名男学生?22. 某校计划购买篮球和排球两种球若干.已知购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同.(1)、求篮球和排球的单价;(2)、该校计划购买篮球和排球共30个.某商店有两种优惠活动(两种优惠活动不能同时参加),活动一:一律打九折,活动二:购物不超过600元时不优惠,超过600元时,超过600元的部分打八折.请根据以上信息,说明选择哪一种活动购买篮球和排球更实惠.23. 如图,已知 ,现将一直角三角形 放入图中,其中 , 交 于点 , 交 于点F. (1)、当 所放位置如图一所示时,则 与 的数量关系为;(2)、当 所放位置如图二所示时,试说明: ;(3)、在(2)的条件下,若 与 交于点 ,且 , ,求 的度数.
(1)、当 所放位置如图一所示时,则 与 的数量关系为;(2)、当 所放位置如图二所示时,试说明: ;(3)、在(2)的条件下,若 与 交于点 ,且 , ,求 的度数.