2020年暑期衔接训练青岛版数学八年级下册：第4讲 第六章《平行四边形》单元测试
试卷更新日期：2020-07-07 类型：复习试卷
一、单选题
-
1. 下是关于某个四边形的三个结论：①它的对角线相等；②它是一个正方形；③它是一个矩形.下列推理过程正确的是（ ）A、由②推出③，由③推出① B、由①推出②，由②推出③ C、由③推出①，由①推出② D、由①推出③，由③推出②2. 顺次连结对角线互相垂直的四边形各边中点所构成的四边形一定是（ ）A、矩形 B、菱形 C、正方形 D、不确定3. 如图，已知四边形ABCD，R，P分别是DC，BC上的点，E，F分别是AP，RP的中点，当点P在BC上从点B向点C移动而点R不动时， 那么下列结论成立的是（ ）．
A、线段EF的长逐渐增大 B、线段EF的长逐渐减少 C、线段EF的长不变 D、线段EF的长不能确定4. 如图，在△ABC中，点D在BC上，DE∥AC，DF∥AB，下列四个判断中错误的是（ ）
A、四边形AEDF是平行四边形 B、若∠BAC＝90°，则四边形AEDF是矩形 C、若AD平分∠BAC，则四边形AEDF是矩形 D、若AD⊥BC且AB＝AC，则四边形AEDF是菱形5. 如图，四边形 和 都是平行四边形，过点 作直线交边 于点 ，交边 于点 ，连接 ， .若 和 的面积分别为4和6，则 的面积为（ ）
A、5 B、5.5 C、6 D、86. 已知：∠MON，如图，小静进行了以下作图：①在∠MON的两边上分别截取OA，OB，使OA=OB；
②分别以点A，B为圆心，OA长为半径作弧，两弧交于点C；
③连接AC，BC，AB，OC．
若OC=2，S四边形OACB=4，则AB的长为（ ）
A、5 B、4 C、3 D、27. 四边形具有不稳定性，对于四条边长确定的四边形，当内角度数发生变化时，其形状也会随之改变，如图，改变正方形ABCD的内角，正方形ABCD变为菱形ABC′D′，若∠D′AB＝30°，则菱形ABC′D′的面积与正方形ABCD的面积之比是（ ）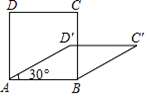
A、1 B、 C、 D、8. 如图，在 ABCD中，对角经AC，BD交于点O，BD=2AD，点E，F，G分别是OA，OB，CD的中点，EG交FD于点H。有下列4个结论：①ED⊥CA；②EF=EG；③FH= FD；④S△EFD= S△CED ， 其中说法正确的有（ ）
A、1个 B、2个 C、3个 D、4个9. 如图，正方形ABCD的边长为2，P为CD的中点，连结AP，过点B作BE⊥AP于点E，延长CE交AD于点F，过点C作CH⊥BE于点G，交AB于点H，连接HF。下列结论正确的是（ ）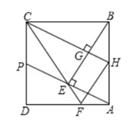
A、CE= B、EF= C、cos∠CEP= D、HF2=EF·CF10. 如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相交于点H，给出下列结论：①BE=2AE②△DFP∽△BPH③△PFD∽△PDB④DP2=PH·PC其中正确的有（ ）
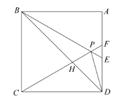A、①②③④ B、②③ C、①②④ D、①③二、填空题
-
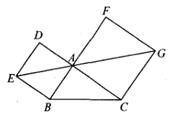
11. 已知菱形ABCD的对角线AC＝12 cm，BD=16cm，则这个菱形的面积为cm.12. 如图，在△ABC中，分别以AB，AC为边向外作正方形ABED，ACGF。若点E，A，G在同一直线上，EG=8 ，BC=7，则△ABC的面积为。
13. 如图，在四边形 中，点E、F分别是线段AD、BC的中点，G、H分别是线段BD、AC的中点，当四边形 的边满足时，四边形 是菱形.
14. 在四边形ABCD中，对角线AC ⊥BD且AC=4，BD=8，E、F分别是边AB.CD的中点，则EF= .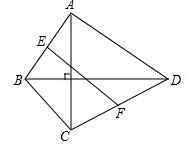
15. 如图，平行四边形ABCD中，AB=8cm，AD=12cm，点P在AD边上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在运动以后，以P、D、Q、B四点组成平行四边形的次数有次.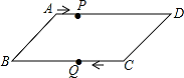
三、解答题
-
16. 如图，在平行四边形ABCD中，AC、BD交于点O，又M、N分别是OA、OC的中点.
(1)、求证：BM＝DN；(2)、若AO＝BD，试判断四边形MBND的形状，并证明你的结论.17. 如图， 为菱形 对角线的交点， ， .
(1)、试判断四边形 的形状，并说明理由；(2)、若 ， ，求线段 的长.18. 已知，如图1，D是△ABC的边上一点，CN∥AB，DN交AC于点M，MA＝MC.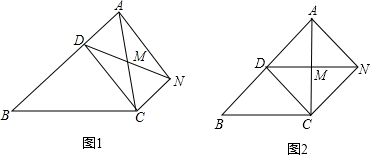
(1)、求证：四边形ADCN是平行四边形.(2)、如图2，若∠AMD＝2∠MCD，∠ACB＝90°，AC＝BC.请写出图中所有与线段AN相等的线段（线段AN除外）
