河南省驻马店市平舆县2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-07 类型：期末考试

进入出卷网下载

一、选择题

1. 在平面直角坐标系中，点 $P (- 3 ， 2)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列各数中最小的数是（）

A、 $- π$ B、-3 C、 $- \sqrt{7}$ D、0

查看试题解析
3. 下面的调查中，不适合抽样调查的是（）

A、一批炮弹的杀伤力的情况 B、了解一批灯泡的使用寿命 C、全国的人口普查 D、全市学生每天参加体育锻炼的时间

查看试题解析
4. 下列不等式的变形正确的是（）

A、由a﹥b,得ac﹥bc B、由a﹥b,得a-2﹥b-2 C、由 $- \frac{1}{2}$ ﹥-1,得 $- \frac{x}{2} > - x$ D、由a﹥b,得c-a﹥c-b

查看试题解析
5. 已知 $x ， y$ 为实数，且 $\sqrt{x - 3} + {(y + 2)}^{2} = 0$ ，则 $y^{x}$ 的立方根是（）

A、 $3 \sqrt{6}$ B、－8 C、－2 D、 $\pm 2$

查看试题解析
6. 如图，若图形A经过平移与下方图形拼成一个长方形，则正确的平移方式是（）

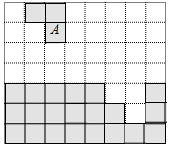A、向右平移4格，再向下平移4格 B、向右平移6格，再向下平移5格 C、向右平移4格，再向下平移3格 D、向右平移5格，再向下平移3格

查看试题解析
7. 若 $3 x^{2 a + b} y^{2}$ 与 $4 x^{3} y^{3 a - b}$ 是同类项，则a-b=（）

A、0 B、1 C、2 D、3

查看试题解析
8. 如图，点E在AB的延长线上，下列条件中能判断AD∥BC的是（）

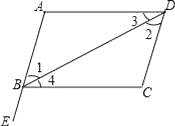A、∠1=∠2 B、∠3=∠4 C、∠C=∠CBE D、∠C+∠ABC=180°

查看试题解析
9. 关于x的不等式组 ${\begin{matrix} 3 x - 1 > 4 (x - 1) \\ x < m \end{matrix}$ 的解集为x＜3，那么m的取值范围为（）

A、m=3 B、m＞3 C、m＜3 D、m≥3

查看试题解析
10. 某市举办画展，如图，在长 $14 m$ ，宽 $10 m$ 的长方形展厅中，划出三个形状大小完全一样的小长方形区域摆放水仙花，则每个小长方形的周长为（）

A、 $8 m$ B、 $13 m$ C、 $16 m$ D、 $20 m$

查看试题解析
11. $\sqrt{81}$ 的算术平方根是， $\sqrt[3]{1 +2 \frac{3}{8}}$ =.

查看试题解析
12. 已知 $A B / / x$ 轴，点 $A$ 的坐标为 $(2, 5)$ ，并且 $A B = 4$ ，则点B的坐标为.

查看试题解析
13. 如果m，n为实数，且满足 $| m + n + 2 | + {(m - 2 n + 8)}^{2} = 0$ ，则 $m n =$ .

查看试题解析
14. 已知关于x的不等式组 ${\begin{matrix} x - a \geq 0 \\ 3 - 2 x \geq - 1 \end{matrix}$ 的整数解共有5个，则a的取值范围是．

查看试题解析
15. 我国明代数学家程大位的名著《直指算法统宗》里有一道著名算题：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”意思是：有100个和尚分100个馒头，如果大和尚一人分3个，小和尚3人分1个，正好分完，试问大、小和尚各几人？设大、小和尚各有 $x$ ， $y$ 人，则可以列方程组.

查看试题解析

二、解答题

16.

(1)、计算： $\sqrt[3]{- 0.125} + | \sqrt{3} - 2 | - \sqrt{3 - \frac{3}{4}} + | \sqrt{3} | - \sqrt{{(- 2)}^{2}}$ ；

(2)、解方程： ${\begin{matrix} 4 x - 3 y = 11 \\ 2 x + y = 13 \end{matrix}$ .

查看试题解析
17. 解不等式组，并将解集表示在数轴上.
${\begin{matrix} 2 (x + 8) \leq 10 - 4 (x - 3) \\ \frac{x + 1}{3} - \frac{3 x + 1}{2} < 1 \end{matrix}$

查看试题解析
18. 已知关于 $x$ ， $y$ 的二元一次方程组 ${\begin{matrix} 2 x - y = 4 m - 5, \\ x + 4 y = - 7 m + 2 \end{matrix}$ 的解满足 $x + y > - 3$ ，其中 $m$ 是非负整数，求 $m$ 的值.

查看试题解析
19. 已知：如图所示，DE⊥AC于点E，BC⊥AC于点C，FG⊥AB于点G，∠1=∠2，试说明CD⊥AB.

查看试题解析
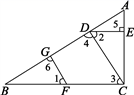20. 解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度，随机抽取了部分学生进行调查（每人限选1项），现将调查结果绘制成如下两幅不完整的统计图，根据图中所给的信息解答下列问题．

(1)、喜爱动画的学生人数和所占比例分别是多少？

(2)、请将条形统计图补充完整；

(3)、若该校共有学生1000人，依据以上图表估计该校喜欢体育的人数约为多少？

查看试题解析
21. 如图，在正方形网络中，每个小方格的的边长为1个单位长度， $Δ A B C$ 的顶点A，B的坐标分别为(0，5)，(-2，2).

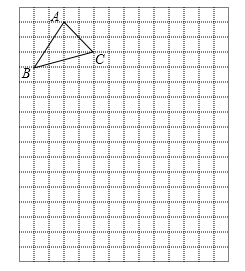(1)、请在图中建立平面直角坐标系，并写出点 $C$ 的坐标：.

(2)、平移 $Δ A B C$ ，使点 $C$ 移动到点 $F (7 ， - 4)$ ，画出平移后的 $Δ D E F$ ，其中点D与点A对应，点E与点B对应.

(3)、求 $Δ A B C$ 的面积.

(4)、在坐标轴上是否存在点 $P$ ，使 $Δ P O C$ 的面积与 $Δ A B C$ 的面积相等，若存在，请直接写出点 $P$ 的坐标；若不存在，请说明理由.

查看试题解析
22.

(1)、①如图1，已知 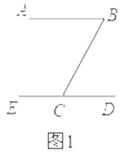$A B ∥ C D$ ， $∠ A B C = 60 °$ ，可得 $∠ B C D =$ .

②如图2，在①的条件下，如果 $C M$ 平分 $∠ B C D$ ，则 $∠ B C M =$ .

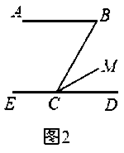
③如图3，在①、②的条件下，如果 $C N ⊥ C M$ ，则 $∠ B C N =$ .

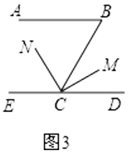(2)、尝试解决下面问题：已知如图4， $A B ∥ C D$ ， $∠ B = 40 °$ ， $C N$ 是 $∠ B C E$ 的平分线， $C N ⊥ C M$ ，求 $∠ B C M$ 的度数.

查看试题解析
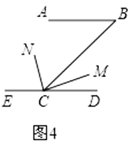23. 为解决中小学大班额问题，东营市各县区今年将改扩建部分中小学，某县计划对A、B两类学校进行改扩建，根据预算，改扩建2所A类学校和3所B类学校共需资金7800万元，改扩建3所A类学校和1所B类学校共需资金5400万元.

(1)、改扩建1所A类学校和1所B类学校所需资金分别是多少万元？

(2)、该县计划改扩建A、B两类学校共10所，改扩建资金由国家财政和地方财政共同承担，若国家财政拨付资金不超过11800万元，地方财政投入资金不少于4000万元，其中地方财政投入到A、B两类学校改扩建资金分别为每所300万元和500万元，请问共有哪几种改扩建方案？

查看试题解析