河南省镇平县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-07 类型:期末考试
一、选择题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是 )A、
 B、
B、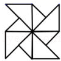 C、
C、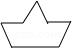 D、
D、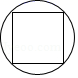
-
2. 方程2x-2=4的解是( )A、x=2 B、x=3 C、x=4 D、x=5
-
3. 下列各组数中,能作为一个三角形三边边长的是( )
A、1,1,2 B、1,2,4 C、2,3,4 D、2,3,5 -
4. 将某不等式组的解集 表示在数轴上,下列表示正确的是( )A、
 B、
B、 C、
C、 D、
D、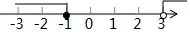
-
5. 一个正n边形的每一个外角都是36°,则n=( )A、7 B、8 C、9 D、10
-
6. 小刚准备用自己节省的零花钱购买一台MP4来学习英语,他已存有50元,并计划从本月起每月节省30元,直到他至少有280元.设x个月后小刚至少有280元,则可列计算月数的不等式为( )A、30x+50>280 B、30x﹣50≥280 C、30x﹣50≤280 D、30x+50≥280
-
7. 阳光中学阅览室在装修过程中,准备用边长相等的正方形和正三角形两种地砖镶嵌地面,在每个顶点的周围正方形、正三角形地砖的块数可以分别是( )A、2,2 B、2,3 C、1,2 D、2,1
-
8. 若a-b>a,a+b<b,则有( ).A、ab<0 B、 >0 C、a+b>0 D、a-b<0
-
9. 如图,将Rt ABC绕直角顶点C顺时针旋转90°,得到 A' B'C,连接AA',若∠1=20°,则∠B的度数是( )
 A、70° B、65° C、60° D、55°
A、70° B、65° C、60° D、55° -
10. 一个两位数,个位上的数字与十位上的数字之和为7,如果这个两位数加上45则恰好成为个位数字与十位数字对调后组成的新两位数,则原来的两位数是( )A、61 B、16 C、52 D、25
二、填空题
-
11. 若关于x的方程 的解是正数,则k的取值范围是.
-
12. 若关于x、y的二元一次方程3x﹣ay=1有一个解是 ,则a=.
-
13. 已知三角形两边的长分别是3和7,如果此三角形第三边的长取最大的整数,则这个数是.
-
14. 一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是 .
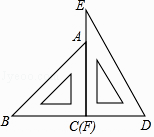
-
15. 某种商品每件的标价是270元,按标价的八折销售时,仍可获利20%,则这种商品每件的进价为元.
三、解答题
-
16. 解方程或方程组:(1)、 ;(2)、
-
17. 如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
 (1)、试在图中标出点D,并画出该四边形的另两条边;(2)、将四边形ABCD向下平移5个单位长度,画出平移后得到的四边形A′B′C′D′.
(1)、试在图中标出点D,并画出该四边形的另两条边;(2)、将四边形ABCD向下平移5个单位长度,画出平移后得到的四边形A′B′C′D′. -
18. 解不等式或不等式组,并把它的解集表示在数轴上:(1)、 ;(2)、
-
19. 某织布厂有150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30m,或利用所织布制衣4件,制衣一件需要布1.5m,将布直接出售,每米布可获利2元,将布制成衣后出售,每件可获利25元,若每名工人每天只能做一项工作,且不计其他因素,设安排x名工人制衣.(1)、一天中制衣所获利润P是多少(用含x的式子表示);(2)、一天中剩余布所获利润Q是多少 (用含x的式子表示);.(3)、一天当中安排多少名工人制衣时,所获利润为11806元?
-
20. 一个正多边形中,一个内角的度数是它相邻的一个外角的度数的3倍.(1)、求这个多边形的每一个外角的度数;(2)、求这个多边形的边数.
-
21. 某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)、试计算两种笔记本各买了多少本?(2)、请你解释:小明为什么不可能找回68元? -
22. 如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.已知 , , 设 ,求 和 的大小.

-
23. 某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.(1)、九年级师生表演的歌唱类与舞蹈类节目数各有多少个?(2)、该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目演出的平均用时分别为5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟,若从20:00开始,22:30之前演出结束,问参与的小品类节目最多有多少个?
