浙江省杭州市江干区2020年数学中考模拟试卷（4月）

试卷更新日期：2020-07-07 类型：中考模拟

进入 出卷网 下载

一、选择题

  • 1. 用科学记数法表示202000为（　　）
    A、202×1000 B、2.02×105 C、2.02×104 D、（2.02）5

    查看试题解析

  • 2. 下列运算正确的是（　　）
    A、m2•m3＝m6 B、（m2）3＝m5 C、m3÷m2＝m D、3m﹣m＝2

    查看试题解析

  • 3. 估计与 27 最接近的整数是（  ）
    A、4 B、5 C、6 D、7

    查看试题解析

  • 4. 实数a，b在数轴上的对应点的位置如图所示，则下列结论正确的是（　　）

    A、a＞b B、a＞﹣b C、|a|＜|b| D、a＜﹣2

    查看试题解析

  • 5. 若数据：2，2，x，3，4的平均数为3，则这组数中的（　　）
    A、中位数为3 B、众数为3 C、x＝3 D、中位数为x

    查看试题解析

  • 6. 有一个转盘如图，让转盘自由转动两次，则指针两次都落在黄色区域的概率是（　　）

    A、14 B、49 C、23 D、56

    查看试题解析

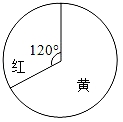  • 7. 如图，嘉淇一家驾车从A地出发，沿着北偏东60°的方向行驶，到达B地后沿着南偏东50°的方向行驶来到C地，且C地恰好位于A地正东方向上，则下列说法正确的是（　　）

    A、B地在C地的北偏西40°方向上       B、A地在B地的南偏西30°方向上       C、cos∠BAC=32 D、∠ACB＝50°

    查看试题解析

  • 8. 如图，分别以等边三角形ABC的三个顶点为圆心，以边长为半径画弧，得到的封闭图形是莱洛三角形，若AB＝2，则莱洛三角形的面积（即阴影部分面积）为（　　）

    A、π+3 B、π−3 C、2π−3 D、2π−23

    查看试题解析

  • 9. 如图，直l1∥l2 ， 点A、B固定在直线l2上，点C是直线11上一动点，若点E、F分别为CA、CB中点，对于下列各值：①线段EF的长；②△CEF的周长；③△CEF的面积；④∠ECF的度数，其中不随点C的移动而改变的是（　　）

    A、①② B、①③ C、②④ D、③④

    查看试题解析

  • 10. 已知⊙O的半径为3，A为圆内一定点，AO＝1，P为圆上一动点，以AP为边作等腰△APQ，AP＝PQ，∠APQ＝120°，则OQ的最大值为（　　）
    A、1+33 B、1+23 C、3+3 D、33−1

    查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分.

  • 11. 化简： a−1a+1a ＝.

    查看试题解析

  • 12. 因式分解：a3﹣4a=  ．

    查看试题解析

  • 13. 如图，AB是半圆O的直径，点C是半圆O上一点，点D是弧BC的中点，∠BAC＝50°.则∠ABD＝.

    查看试题解析

  • 14. 如图，▱ABCD的对角线AC、BD相交于点O，点E是AB的中点，△BEO的周长是8，则△BCD的周长为.

    查看试题解析

  • 15. 如图，已知函数y＝2x与反比例函数y＝ kx （x＞0）的图象交于点A，将y＝2x的图象向下平移6个单位后与反比例函数y═ kx （x＞0）交于点B，与x轴交于点C，若OA＝2BC，则k＝.

    查看试题解析

  • 16. 设a，b是实数，定义@的一种运算如下：a@b＝（a+b）2﹣（a﹣b）2 ， 则下列结论：

    ①若a@b＝0，则a＝0或b＝0；②a@（b+c）＝a@b+a@c；

    ③不存在实数a，b，满足a@b＝a2+5b2；

    ④设a，b是矩形的长和宽，若矩形的周长固定，则当a＝b时，a@b最大.

    其中正确的是.

    查看试题解析

三、解答题：本大题有7个小题，共66分.解答应写出文字说明、证明过程或演算步骤.

  • 17. 在等腰三角形ABC中，底边BC为y，腰长AB长为x，若三角形ABC的周长为12.
    (1)、求y关于x的函数表达式；
    (2)、当腰长比底边的2倍多1时，求x的值.

    查看试题解析

  • 18. 某校七年级随机抽查了若干同学，请他们分别记录自己家中一周内丢弃的塑料袋的数量（单位：个），将收集到的数据绘制成如图所示的两幅不完整的统计图，请你根据图中所给信息解答下列各题：

    (1)、这次调查的人数是多少？
    (2)、将条形统计图补充完整.
    (3)、该校七年级共有650人，估计这周全体七年级学生家中丢弃的塑料袋的数量.

    查看试题解析

  • 19. 某校举办“迎亚运“学生书画展览，现要在长方形展厅中划出3个形状、大小完全一样的小长方形（图中阴影部分）区域摆放作品.

    (1)、如图1，若大长方形的长和宽分别为45米和30米，求小长方形的长和宽.
    (2)、如图2，若大长方形的长和宽分别为a和b

    ①直接写出1个小长方形周长与大长方形周长之比；

    ②若作品展览区域（阴影部分）面积占展厅面积的 13 ，试求 xy 的值.

    查看试题解析

  • 20. 如图，在Rt△ABC中，∠ACB＝90°.∠ABC的平分线交AC于点O，以点O为圆心，OC为半径.在△ABC同侧作半圆O.

    (1)、求证：AB与⊙O相切；
    (2)、若AB＝5，AC＝4，求⊙O的半径.

    查看试题解析

  • 21. 已知一张正方形ABCD纸片，边长AB＝2，按步骤进行折叠，如图1，先将正方形纸片ABCD对折，得到折痕EF；再折出矩形BCFE的对角线BF.

    (1)、如图2，将CF边折到BF上，得到折痕FM，点C的对应点为C'，求CM的长.
    (2)、如图3，将AB边折到BF上，得到折痕BN，点A的对应点为A'，求AN的长.

    查看试题解析

  • 22. 已知二次函数y＝﹣x2+2tx﹣t+1（是常数）.
    (1)、求此函数的顶点坐标.（用含t的代数式表示）
    (2)、当x≥2时，y随x的增大而减小，求t的取值范围.
    (3)、当0≤x≤1时，该函数有最大值4，求t的值.

    查看试题解析

  • 23. 已知：如图，在Rt△ABC和Rt△ABD中，∠ACB＝90°，∠ABD＝90°，AB＝BD，BC＝4，（点A、D分别在直线BC的上下两侧），点G是Rt△ABD的重心，射线BG交边AD于点E，射线BC交边AD于点F.

    (1)、求证：∠CAF＝∠CBE；
    (2)、当点F在边BC上，AC＝1时，求BF的长；
    (3)、若△BGC是以BG为腰的等腰三角形，试求AC的长.

    查看试题解析