浙江省杭州市拱墅区锦绣育才教育集团2020年数学中考二模试卷

试卷更新日期：2020-07-07 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣3的相反数是（）

A、﹣3 B、3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 已知⊙O的半径为5，若PO=4，则点P与⊙O的位置关系是（）

A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法判断

查看试题解析
3. 已知 $\frac{x - 2 y}{y} = \frac{2}{5}$ ，则 $\frac{x}{y}$ 的值为（　　）

A、 $\frac{5}{4}$ B、 $\frac{4}{5}$ C、 $\frac{5}{12}$ D、 $\frac{12}{5}$

查看试题解析
4. 将二次函数y＝5x²的图象先向右平移2个单位，再向下平移3个单位，得到的函数图象的解析式为（）

A、y＝5（x+2）²+3 B、y＝5（x﹣2）²+3 C、y＝5（x+2）²﹣3 D、y＝5（x﹣2）²﹣3

查看试题解析
5. 在一个不透明的盒子中装有8个白球，若干个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球为白球的概率是 $\frac{2}{3}$ ，则黄球的个数为（　　）

A、16 B、12 C、8 D、4

查看试题解析
6. 如图，AD∥BE∥CF，点B，E分别在AC，DF上，DE＝2，EF＝AB＝3，则BC长为（　　）

A、 $\frac{9}{2}$ B、2 C、 $\frac{7}{2}$ D、4

查看试题解析
7. 如图，点A，B，C，P在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE＝40°，则∠P的度数为（　　）

A、70° B、60° C、40° D、35°

查看试题解析
8. 已知抛物线y＝ax²+bx+c与反比例函数y＝ $\frac{b}{x}$ 的图象在第一象限有一个公共点，其横坐标为1，则一次函数y＝bx+ac的图象可能是（　　）

A、 B、 C、 D、

查看试题解析
9. 如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足S_△_PAB＝ $\frac{1}{3}$ S_矩形_ABCD ，则点P到A、B两点距离之和PA+PB的最小值为（）

A、 $\sqrt{29}$ B、 $\sqrt{34}$ C、5 $\sqrt{2}$ D、 $\sqrt{41}$

查看试题解析
10. 已知二次函数y=（x﹣h）²+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（）

A、1或﹣5 B、﹣1或5 C、1或﹣3 D、1或3

查看试题解析

二、填空题（共6小题）

11. 若sinα＝ $\sqrt{2}$ cos60°，则锐角α＝.

查看试题解析
12. 已知点P是线段AB的黄金分割点，PA＞PB，AB＝2cm，那么PA＝cm.

查看试题解析
13. 分解因式：12m²n²﹣12m²n+3m²＝.

查看试题解析
14. 扇形的圆心角为150°，弧长为20π，则扇形的面积为（可保留π）.

查看试题解析
15. 如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD.已知DE＝6，∠BAC+∠EAD＝180°，则弦BC的弦心距等于.

查看试题解析
16. 如图，在矩形纸片ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：
①∠EBG＝45°；

②△DEF∽△ABG；

③S_△_ABG＝S_△_FGH；

④AG+DF＝FG.

其中正确的是.（填写正确结论的序号）

查看试题解析

三、解答题（共7小题）

17. 先化简，再求值： $\frac{a + 1}{a^{2} - 2 a + 1} \div (1 + \frac{2}{a - 1})$ ，其中a＝3.

查看试题解析

18. 某校七、八年级各有10名同学参加市级数学竞赛，各参赛选手的成绩如下（单位：分）：

七年级：89，92，92，92，93，95，95，96，98，98

八年级：88，93，93，93，94，94，95，95，97，98

整理得到如下统计表

年级	最高分	平均分	中位数	众数	方差
七年级	98	94	a	m	7.6
八年级	98	n	94	93	6.6

根据以上信息，完成下列问题

(1)、填空：a＝；m＝；n＝；

(2)、两个年级中，年级成绩更稳定；

(3)、七年级两名最高分选手分别记为：A₁ ， A₂ ，八年级第一、第二名选手分别记为B₁ ， B₂ ，现从这四人中，任意选取两人参加市级经验交流，请用树状图法或列表法求出这两人分别来自不同年级的概率.

查看试题解析

19. 如图，甲、乙两座建筑物的水平距离BC为78m.从甲的顶部A处测得乙的顶部D处的俯角为48°，测得底部C处的俯角为58°，求甲、乙建筑物的高度AB和DC.
（结果取整数，参考数据：tan48°≈1.1，tan58°≈1.60）

查看试题解析
20. 甲、乙两车同时从A地出发，匀速开往B地，甲车行驶到B地后立即沿原路线以原速度返回A地，到达A地后停止运动：当甲车到达A地时，乙车恰好到达B地，并停止运动.已知甲车的速度为150km/h，设甲车出发xh后，甲、乙两车之间的距离为ykm，图中的折线OMNQ表示了整个运动过程中y与x之间的函数关系.

(1)、A、B两地的距离是km，乙车的速度是km/h；

(2)、指出点M的实际意义，并求线段MN所表示的y与x之间的函数表达式；

(3)、当两车相距50km时，直接写出x的值.

查看试题解析
21. 如图，AD是△ABC的外接圆⊙O的直径，点P在BC延长线上，且满足∠PAC＝∠B.

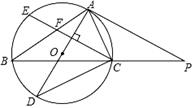(1)、求证：PA是⊙O的切线；

(2)、弦CE⊥AD交AB于点F，若AF•AB＝12，求AC的长.

查看试题解析
22. 已知在同一平面直角坐标系中有函数y₁＝ax²﹣2ax+b，y₂＝﹣ax+b，其中ab≠0.

(1)、求证：函数y₂的图象经过函数y₁的图象的顶点；

(2)、设函数y₂的图象与x轴的交点为M，若点M关于y轴的对称点M'在函数y₁图象上，求a，b满足的关系式；

(3)、当﹣1＜x＜1时，比较y₁与y₂的大小.

查看试题解析
23. 已知正方形ABCD，点M为边AB的中点.

(1)、如图1，点G为线段CM上的一点，且∠AGB＝90°，延长AG、BG分别与边BC、CD交于点E、F.
①求证：BE＝CF；

②求证：BE²＝BC•CE.

(2)、如图2，在边BC上取一点E，满足BE²＝BC•CE，连接AE交CM于点G，连接BG并延长交CD于点F，求tan∠CBF的值.

查看试题解析