浙江省杭州市2020年数学中考模拟试卷（5月）

试卷更新日期：2020-07-07 类型：中考模拟

进入出卷网下载

一、选择题（每题3分，满分30分）

1. $- \frac{4}{3}$ 的相反数是（　　）

A、 $- \frac{3}{4}$ B、 $\frac{3}{4}$ C、 $\frac{4}{3}$ D、 $- \frac{4}{3}$

查看试题解析
2. 已知⊙O的半径为3，A为线段PO的中点，则当OP＝5时，点A与⊙O的位置关系为（　　）

A、点在圆内 B、点在圆上 C、点在圆外 D、不能确定

查看试题解析
3. 已知2x＝3y，则下列比例式成立的是（　　）

A、 $\frac{x}{2} = \frac{3}{y}$ B、 $\frac{x}{2} = \frac{y}{3}$ C、 $\frac{x}{3} = \frac{y}{2}$ D、 $\frac{x}{y} = \frac{2}{3}$

查看试题解析
4. 把抛物线y＝x²向上平移3个单位，再向右平移1个单位，则平移后抛物线的解析式为（　　）

A、y＝（x+3）²+1 B、y＝（x+3）²﹣1 C、y＝（x﹣1）²+3 D、y＝（x+1）²+3

查看试题解析
5. 在一只不透明的口袋中放入只有颜色不同的白球6个，黑球8个，黄球n个，搅匀后随机从中摸取一个恰好是黄球的概率为 $\frac{1}{3}$ ，则放入的黄球个数?＝（　　）

A、4 B、5 C、6 D、7

查看试题解析
6. 如图，AB∥GH∥CD，点H在BC上，AC与BD交于点G，AB＝2，CD＝3，则GH长为（　　）

A、1 B、1.2 C、2 D、2.5

查看试题解析
7. 如图，AB是⊙O的直径，点C在⊙O上，CD平分∠ACB交⊙O于点D，若∠ABC＝30°，则∠CAD的度数为（　　）

A、100° B、105° C、110° D、120°

查看试题解析
8. 已知反比例函数y＝ $\frac{k}{x}$ 的图象在每一个象限内，y随x的增大而增大，那么一次函数y＝kx+2的大致图象是（　　）

A、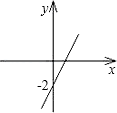 B、 C、 D、

查看试题解析
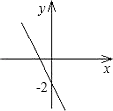9. 如图，△ABC是等边三角形，AD是BC边上的高，点E是AC边的中点，点P是AD上的一个动点，当PC+PE最小时，∠CPE的度数是（　　）

A、30° B、45° C、60° D、90°

查看试题解析
10. 已知关于n的函数s＝an²+bn（n为自然数），当n＝9时，s＜0；当n＝10时，s＞0.则n取（　　）时，s的值最小.

A、3 B、4 C、5 D、6

查看试题解析

二、填空题（满分18分，每小题3分）

11. 已知∠A为锐角，且tanA＝ $\sqrt{3}$ ，则∠A的大小为.

查看试题解析
12. 如果点P是线段AB的黄金分割点（AP＞BP），那么 $\frac{B P}{A P}$ 的值是.

查看试题解析
13. 把ab²﹣ab分解因式的结果是.

查看试题解析
14. 如图，在半径为 $\sqrt{10}$ ，圆心角等于45°的扇形AOB内部作一个矩形CDEF，使点C在OA上，点D、E在OB上，点F在弧AB上，且DE＝2CD，则：

(1)、弧AB的长是（结果保留π）；

(2)、图中阴影部分的面积为（结果保留π）.

查看试题解析
15. 如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB＝30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点.若⊙O的半径为7，则GE+FH的最大值为.

查看试题解析
16. 如图，在矩形ABCD的边AB上有一点E，且 $\frac{A E}{E B} = \frac{3}{2}$ ，DA边上有一点F，且EF＝18，将矩形沿EF对折，A落在边BC上的点G，则AB＝.

查看试题解析

三、解答题

17. 先化简，再求值：（x﹣2+ $\frac{8 x}{x - 2}$ ）÷ $\frac{x + 2}{2 x - 4}$ ，其中x＝ $- \frac{1}{2}$ .

查看试题解析

18. 一次安全知识测验中，学生得分均为整数，满分10分，成绩达到9分为优秀，这次测验中甲、乙两组学生人数相同，成绩如下两个统计图：

(1)、在乙组学生成绩统计图中，8分所在的扇形的圆心角为度；

(2)、请补充完整下面的成绩统计分析表：

	平均分	方差	众数	中位数	优秀率
甲组	7	1.8	7	7	20%
乙组		1.36			10%

(3)、你认为哪组的成绩较好？从以上信息中写出两条支持你的选择.

(4)、从甲乙两组得9分的学生中抽取两人参加市级比赛，求这两人来自不同组的概率.

查看试题解析

19. 某数学社团成员想利用所学的知识测量某广告牌的宽度（图中线段MN的长），直线MN垂直于地面，垂足为点P ．在地面A处测得点M的仰角为58°、点N的仰角为45°，在B处测得点M的仰角为31°，AB＝5米，且A、B、P三点在一直线上．请根据以上数据求广告牌的宽MN的长．
（参考数据：sin58°＝0.85，cos58°＝0.53，tan58°＝1.60，sin31°＝0.52，cos31°＝0.86，tan31°＝0.60．）

查看试题解析
20. 甲乙两位老师同住一小区，该小区与学校相距2000米.甲从小区步行去学校，出发10分钟后乙再出发，乙从小区先骑公共自行车，骑行若干米到达还车点后，立即步行走到学校.已知乙骑车的速度为170米/分，甲步行的速度比乙步行的速度每分钟快5米.设甲步行的时间为x（分），图1中线段OA与折线B﹣C﹣D分别表示甲、乙离小区的路程y（米）与甲步行时间x（分）的函数关系的图象；图2表示甲、乙两人之间的距离s（米）与甲步行时间x（分）的函数关系的图象（不完整）.

根据图1和图2中所给的信息，解答下列问题：

(1)、求甲步行的速度和乙出发时甲离开小区的路程；

(2)、求直线BC的解析式；

(3)、在图2中，画出当20≤x≤25时，s关于x的函数的大致图象.

查看试题解析
21. 如图，在⊙O中，AB是直径，BC是弦，BC＝BD，连接CD交⊙O于点E，∠BCD＝∠DBE.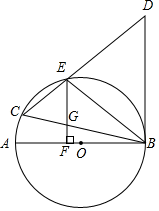

(1)、求证：BD是⊙O的切线.

(2)、过点E作EF⊥AB于F，交BC于G，已知DE＝ $2 \sqrt{10}$ ，EG＝3，求BG的长.

查看试题解析
22. 已知抛物线C：y₁＝﹣x²+bx+4.

(1)、如图，抛物线与x轴相交于两点（1﹣m，0）、（1+m，0）.
①求b的值；

②当n≤x≤n+1时，二次函数有最大值为3，求n的值.

(2)、已知直线l：y₂＝2x﹣b+9，当x≥0时，y₁≤y₂恒成立，求b的取值范围.

查看试题解析
23. 已知，在Rt△ABC中，∠A＝90°，点D在BC边上，点E在AB边上，∠BDE= $\frac{1}{2}$ ∠C，过点B作BF⊥DE交DE的延长线于点F.

(1)、如图1，当AB＝AC时：
①∠EBF的度数为；

②求证：DE＝2BF.

(2)、如图2，当AB＝kAC时，求 $\frac{B F}{D E}$ 的值（用含k的式子表示）.

查看试题解析