浙江省宁波市2020年数学中考模拟试卷

试卷更新日期：2020-07-07 类型：中考模拟

进入 出卷网 下载

一、选择题（每小题4分，共40分。）

  • 1. 下列各数是无理数的是（   ）
    A、3.14 B、227 C、- 4 D、5

    查看试题解析

  • 2. 预计到2025年，中国5G用户将超过460000000，将460000000用科学记数法表示为（   ）
    A、4.6×108 B、46×107 C、4.6×109 D、0.46×109

    查看试题解析

  • 3. 如图所示方式，把图1中正方体的一个角切割掉，形成了如图2的几何体， 则如图2的俯视图是（   ）

    A、 B、 C、 D、

    查看试题解析

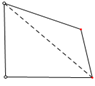  • 4. 用不等式表示图中的解集，其中正确的是（　　）

    A、x≥﹣2 B、x≤﹣2 C、x＜﹣2 D、x＞﹣2

    查看试题解析

  • 5. 掷一枚质地均匀的硬币10次，下列说法正确的是（   ）
    A、必有5次正面朝上 B、可能有5次正面朝上 C、至少有1次正面朝上 D、不可能有10次正面朝上

    查看试题解析

  • 6. 一块三角板（含45°、45°角）和一把直尺摆放位置如图所示，直尺与三角板的一角相交于点A，一边与三角板的两条直角边分别相交于点D、点E，且DE＝2DC，点F在直尺的另一边上，那么∠BFA的大小为（ ）

    A、100° B、120° C、135° D、150°

    查看试题解析

  • 7. 在“新冠肺炎”疫情中，某班30名同学积极捐款，捐款情况统计如下表所示，其中有两个数据被遮盖

    捐款数额（元）

    5

    10

    15

    20

    30

    50

    100

    人数

    ▄

    ▄

    7

    9

    6

    3

    2

    下列关于的统计量中，与被遮盖的数据无关的是（   ）

    A、平均数，方差 B、中位数，方差 C、平均数，众数 D、中位数，众数

    查看试题解析

  • 8. 如图，AB∥EF∥CD，点F在BC上，AC与BD交于点E，AB＝2，CD＝3，则EF长为（   ）


    A、1 B、1.2 C、2 D、2.5

    查看试题解析

  • 9. 使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）（0°＜x≤90°）近似满足函数关系y＝ax2+bx+c（a≠0）.如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（   ）

    A、20° B、36° C、43° D、48°

    查看试题解析

  • 10. 如图，正方形ABCD的边长为2，将正方形ABCD绕着点A旋转到某一位置时，点E恰好分别为DC和B1C1的中点，连结BB1 ， 则BB1的长为（ ）

    A、102 B、  52 C、  2105 D、无法计算

    查看试题解析

二、填空题（每小题5分，共30分）

  • 11. 说明命题“若x＞﹣3，则x2＞9”是假命题的一个反例可以是.

    查看试题解析

  • 12. 已知一块扇形铁皮弧长为30cm，其所在的圆的直径为16cm，用这块铁皮围成一个无底的圆锥形筒，则圆锥形筒的侧面积为cm2 （不计接头）.

    查看试题解析

  • 13. 将黑色棋子按照一定规律排列成一系列如图所示的图案，按照此规律， 第7个图案中黑 色棋子的个数是.

    查看试题解析

  • 14. 如图，已知弧AB所在的圆O半径为2，菱形CMON的顶点C在弧AB上，顶点M，在弦AB上，连接OA，OB，当AM=OM时，则阴影部分的面积是.

    查看试题解析

  • 15. 如图，矩形ABCD中，DE平分∠ADC交BC于点E，将一块三角板的直角顶点放在E点处，并使它的一条直角边过点A，另一条直角边交CD于F点.若点F为CD三等分点，BC＝a，则BE的长为 .（用含a的式子表示）

    查看试题解析

  • 16. 如图，点A是坐标原点，点D是反比例函数y＝ 6x （x＞0）图象上一点，点B在x轴的正半轴上，AD＝BD，四边形ABCD是平行四边形，BC交反比例函数y＝ 6x （x＞0）图象于点E，连接DE，则△DCE的面积为.

    查看试题解析

三、解答题（本大题有8小题，共80分）

  • 17. 解答下列各题：
    (1)、计算： 2−3−|−8|+(2020−π)0−2cos60∘ ;
    (2)、先化简 x2+4x+4x2−4−xx−2 ，再取一个合适的整数x，使得分式的值为整数，并求此时分式的值.

    查看试题解析

  • 18. 如图是由相同的小正方形组成的3 × 3网格，以网格的交错点为顶点的三角形称为格点三角形，请仅用无刻度直尺在网格中完成下列画图.

    (1)、在图1中，画出△ABC中AC边上的中线BE；
    (2)、在图2中，请你画出两个以点G为重心的不同于图1的格点三角形

    (要求所画三角形互不全等）

    查看试题解析

  • 19. 有四张规格、质地相同的卡片，它们的背面完全相同，正面图案分别是A. 任意四边形（每组对边都不平行）， B. 平行四边形， C. 矩形， D. 菱形，将这四张卡片背面朝上洗匀后贴在墙面上（如图所示）.

    (1)、随机抽取一张卡片图案是中心对称的概率是；
    (2)、有甲、乙、丙、丁四位同学从其中一串的最下端取一张卡片，甲第一个取卡片，然后按乙、丙、丁依次取其它三张卡片中的一张，直至取完所有卡片.求丁取得D卡片的概率，并用树状图进行分析说明.

    查看试题解析

  • 20. 如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx﹣ 1a (a<0)与y轴交于点A，将点A向右平移3个单位长度，得到点B，点B在抛物线上.

    (1)、求点B的坐标（用含a的式子表示）和抛物线的对称轴；
    (2)、当B的纵坐标为3时，求a 的值；
    (3)、已知点P（ 12 ，﹣ 1a ），Q（3，3）.若抛物线与线段PQ恰有一个公共点，请结合函数图象直接写出a的取值范围.

    查看试题解析

  • 21. 目前，各大城市都在积极推进公共自行车建设，努力为人们绿色出行带来方便.图（1）所示的是一辆自行车的实物图.图（2）是自行车的车架示意图.CE＝30cm，DE＝20cm，AD＝25cm，DE⊥AC于点E，座杆CF的长为15cm，点A、E、C、F在同一直线上，且∠CAB＝75°，公共自行车车轮的半径约为30cm，且AB与地面平行.

    (1)、求车架中AE的长；
    (2)、求车座点F到地面的距离.（结果精确到1cm.参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）

    查看试题解析

  • 22. 甲、乙两地相距400千米，一辆货车和一辆轿车先后从甲地出发开往乙地，如图，线段OA表示货车离甲地距离y（千米）与货车出发时间x（小时）之间的函数关系：折线BCD表示轿车离甲地距离y（千米）与货车出发时间x （小时）之间的函数关系，请根据图象解答下列问题：

    (1)、货车的速度为千米/时；当轿车刚到乙地时，此时货车距离乙地千米；
    (2)、在轿车到达乙地前，求x为何值时轿车与货车相遇？
    (3)、若两车的距离不超过20千米，求x的取值范围.

    查看试题解析

  • 23. 我们把两个面积相等但不全等的三角形叫关联三角形.

    (1)、如图1，已知等腰直角△ABC，∠ACB=90°，请将它分成两个三角形，使它们成为关联三角形.
    (2)、如图2，已知△ABC为直角三角形，∠ACB=90°，以AB，AC，BC为边向外作正方形ABDE，正方形ACFG和正方形BCMN，连结EG.求证：△ABC与△AEG为关联三角形.
    (3)、在△ABC中，∠A=30°，AC=8，点D在线段AC上，连接BD，△ABD和△BCD是关联三角形，将△ABD沿BD所在的直线翻折，得到△A1BD，若△A1BD与△BCD重合部分的面积等于△BCD面积的一半，求△ABC的面积.

    查看试题解析

  • 24. 如图，在△ABC中，AB=AC，AE是∠BAC的平分线，经过B点的圆O与AE相切于点M，交BC于点G，交AB于点F，FB恰好为圆O的直径，连接BM.

    (1)、求证：BM平分∠ABC.
    (2)、若BC=4，设BM=x，OB=y.

    ① 试求y与x的函数关系式；

    ②当x= 6 时，求sin∠BAC的值.

    (3)、BE+EM= 22 ，求当圆O的半径最小时△ABC的面积.

    查看试题解析