浙江省杭州市西湖区2020年数学中考模拟试卷（3月）

试卷更新日期：2020-07-07 类型：中考模拟

进入出卷网下载

一、选择题（满分30分，每小题3分）

1. 在下列各数0.51515354…、0、 $0. \overset{\cdot}{2}$ 、3π、 $\frac{11}{7}$ 、6.1010010001…、 $\frac{131}{11}$ 、 $\sqrt{27}$ 中，无理数的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 已知：点A（m﹣1，3）与点B（2，n﹣1）关于x轴对称，则（m+n）²⁰¹⁹的值为（）

A、0 B、1 C、﹣1 D、3²⁰¹⁹

查看试题解析
3. 如图是按1：10的比例画出的一个几何体的三视图，则该几何体的侧面积是（）

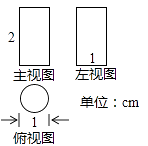A、200cm² B、600cm² C、100πcm² D、200πcm²

查看试题解析
4. 如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝110°，则∠α＝（）

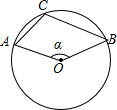A、70° B、110° C、120° D、140°

查看试题解析
5. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
6.
抢微信红包成为节日期间人们最喜欢的活动之一．对某单位50名员工在春节期间所抢的红包金额进行统计，并绘制成了统计图．根据如图提供的信息，红包金额的众数和中位数分别是（）

A、20，20 B、30，20 C、30，30 D、20，30

查看试题解析
7. 如图，在△ABC中，AB的垂直平分线交BC于D，AC的中垂线交BC于E，∠DAE＝20°，则∠BAC的度数为（）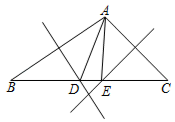

A、70° B、80° C、90° D、100°

查看试题解析
8. 已知三角形的两边长分别是3和4，第三边是方程x²﹣12x+35＝0的一个根，则此三角形的周长是（）

A、12 B、14 C、15 D、12或14

查看试题解析
9. 《孙子算经》中有一道题，原文是：“今有木，不知长短.引绳度之，余绳四尺五寸；屈绳量之，不足一尺.木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，问木长多少尺.设木长为x尺，绳子长为y尺，则下列符合题意的方程组是（）

A、 ${\begin{matrix} y = x + 4.5 \\ \frac{1}{2} y = x + 1 \end{matrix}$ B、 ${\begin{matrix} y = x + 4.5 \\ \frac{1}{2} y = x - 1 \end{matrix}$ C、 ${\begin{matrix} y = 4.5 - x \\ \frac{1}{2} y = x + 1 \end{matrix}$ D、 ${\begin{matrix} y = x - 4.5 \\ \frac{1}{2} y = x - 1 \end{matrix}$

查看试题解析
10. 如图，在同一平面直角坐标系中，一次函数y₁＝kx+b（k、b是常数，且k≠0）与反比例函数y₂＝ $\frac{c}{x}$ （c是常数，且c≠0）的图象相交于A（﹣3，﹣2），B（2，m）两点，则不等式y₁＞y₂的解集是（）

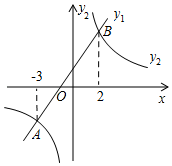A、﹣3＜x＜2 B、x＜﹣3或x＞2 C、﹣3＜x＜0或x＞2 D、0＜x＜2

查看试题解析

二、填空题（满分24分，每小题4分）

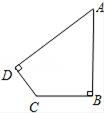
11. 若关于x的二次三项式x²+ax﹣6可分解为（x+3）（x+b）.则a+b＝.

查看试题解析
12. 根据规划，“一带一路”地区覆盖总人口约为4400000000人，这个数用科学记数法表示为．

查看试题解析
13. 学校要从小明、小红与小华三人中随机选取两人作为升旗手，则小明和小红同时入选的概率是.

查看试题解析
14. 甲、乙两台机床同时加工一批直径为100毫米的零件，为了检验产品的质量，从产品中随机抽查6件进行测量，测得的数据如下：（单位：毫米）甲机床：99 98 100 100 103乙机床：99 100 102 99 100 100则加工这批零件性能较好的机床是.

查看试题解析
15. 如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝3， BC＝2，tanA＝ $\frac{4}{3}$ ，则CD＝．

查看试题解析
16. 如图，Rt△ABC中，∠ACB＝90°，BC＝6，AC＝8，现将△ABC折叠，使点A与点B重合，折痕为DE，则tan∠CBE＝.

查看试题解析

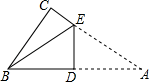
三、解答题

17. 先化简，再求代数式 $\frac{a - 3}{2 a - 4} \div (\frac{5}{a - 2} - a - 2)$ 的值，其中a＝tan60°﹣6sin30°.

查看试题解析
18. 已知：如图，四边形ABCD中，AD∥BC，对角线BD平分∠ABC，且BD⊥DC，E为BC中点，AB＝DE.

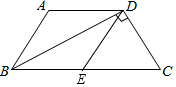(1)、求证：四边形ABED是菱形；

(2)、若∠C＝60°，CD＝4，求四边形ABCD的面积.

查看试题解析
19. 2020年的春节，对于我们来说，有些不一样，我们不能和小伙伴相约一起玩耍，不能去游乐场放飞自我，也不能和自己的兄弟姐妹一起吃美味的大餐，这么做，是因为我们每一个人都在面临一个眼睛看不到的敌人，它叫病毒，残酷的病毒会让人患上肺炎，人与人的接触会让这种疾病快速地传播开来，严重的还会有生命危险，目前我省已经启动突发公共卫生事件一级应急响应，但我们相信，只要大家一起努力，疫情终有会被战胜的一天.
在这个不能出门的悠长假期里，某小学随机对本校部分学生进行“假期中，我在家可以这么做!A.扎实学习、B.快乐游戏、C.经典阅读、D.分担劳动、E.乐享健康”的网络调查，并根据调查结果绘制成如下两幅不完整的统计图（若每一位同学只能选择一项），请根据图中的信息，回答下列问题.

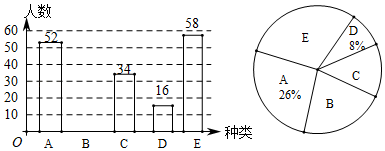(1)、这次调查的总人数是人；

(2)、请补全条形统计图，并说明扇形统计图中E所对应的圆心角是度；

(3)、若学校共有学生的1700人，则选择C有多少人？

查看试题解析
20. 如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB＝∠OBD＝30°，DB＝ $6 \sqrt{3}$ cm.

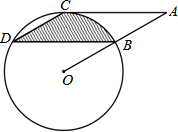(1)、求证：AC是⊙O的切线；

(2)、求由弦CD、BD与弧BC所围成的阴影部分的面积.（结果保留π）

查看试题解析
21. 某校八年级数学兴趣小组在研究等腰直角三角形与图形变换时，作了如下研究：在△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上一动点（点D不与B，C重合），以AD为腰作等腰直角三角形DAF，使∠DAF＝90°，连接CF.

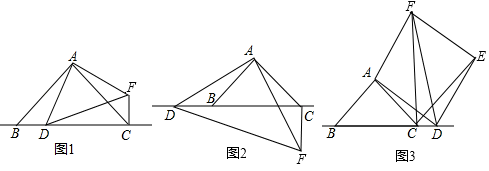(1)、观察猜想
如图1，当点D在线段BC上时，

①CF与BC的位置关系为；

②CF，DC，BC之间的数量关系为（直接写出结论）；

(2)、数学思考
如图2，当点D在线段CB的延长线上时，（1）中的①、②结论是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明.

(3)、拓展延伸
如图3，当点B在线段BC的延长线上时，将△DAF沿线段DF翻折，使点A与点E重合，连接CE，若已知4CD＝BC，AC＝2 $\sqrt{2}$ ，请求出线段CE的长.

查看试题解析
22. 某商店欲购进A、B两种商品，已知购进A种商品5件和B种商品4件共需300元；若购进A种商品6件和B种商品8件共需440元；

(1)、求A、B两种商品每件的进价分别为多少元？

(2)、若该商店，A种商品每件的售价为48元，B种商品每件的售价为31元，且商店将购进A、B共50件的商品全部售出后，要获得的利润超过348元，求A种商品至少购进多少件？

查看试题解析
23. 如图，在平面直角坐标系xOy中，抛物线y＝x²+bx+c与x轴交于A、B两点，与y轴交于点C，对称轴为直线x＝2，点A的坐标为（1，0）.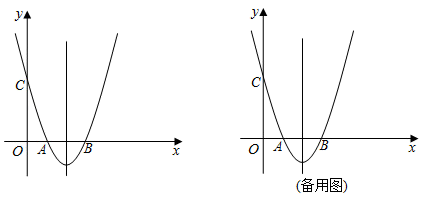

(1)、求该抛物线的表达式及顶点坐标；

(2)、点P为抛物线上一点（不与点A重合），连接PC.当∠PCB＝∠ACB时，求点P的坐标；

(3)、在（2）的条件下，将抛物线沿平行于y轴的方向向下平移，平移后的抛物线的顶点为点D，点P的对应点为点Q，当OD⊥DQ时，求抛物线平移的距离.

查看试题解析