浙江省温州市鹿城区2020届数学中考模拟试卷(二)
试卷更新日期:2020-07-07 类型:中考模拟
一、选择题(共10个题,每题3分,共30分)
-
1. 7的倒数是( )A、- B、7 C、 D、-72. 在下列四个标志中,既是中心对称又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一种病毒长度约为0.000056mm,用科学记数法表示这个数为( )A、5.6×10﹣6 B、5.6×10﹣5 C、0.56×10﹣5 D、56×10﹣64. 下列运算正确的是( )A、 B、 C、 = D、5.
3. 一种病毒长度约为0.000056mm,用科学记数法表示这个数为( )A、5.6×10﹣6 B、5.6×10﹣5 C、0.56×10﹣5 D、56×10﹣64. 下列运算正确的是( )A、 B、 C、 = D、5.如图,将两个形状和大小都相同的杯子叠放在一起,则该实物图的主视图为( )
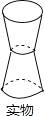 A、
A、 B、
B、 C、
C、 D、
D、 6. 一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )
6. 一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )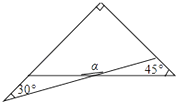 A、165° B、120° C、150° D、135°7. 将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A、165° B、120° C、150° D、135°7. 将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A、y=(x﹣4)2﹣6 B、y=(x﹣4)2﹣2 C、y=(x﹣2)2﹣2 D、y=(x﹣1)2﹣38. 如图,在 中, 的度数为 是 上一点, 是 上不同的两点(不与 两点重合), 的度数为( )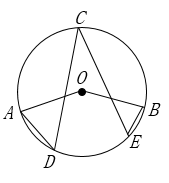 A、m B、 C、 D、9. 已知:如图,在平面直角坐标系 中,等边 的边长为6,点C在边 上,点D在边 上,且 .反比例函数 的图象恰好经过点C和点D.则k的值为 ( )
A、m B、 C、 D、9. 已知:如图,在平面直角坐标系 中,等边 的边长为6,点C在边 上,点D在边 上,且 .反比例函数 的图象恰好经过点C和点D.则k的值为 ( )
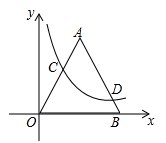 A、 B、 C、 D、10. 小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图),若小亮上坡、平路、下坡的速度分别为 , , , < < ,则小亮同学骑车上学时,离家的路程s与所用时间t的函数关系图象可能是( )
A、 B、 C、 D、10. 小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图),若小亮上坡、平路、下坡的速度分别为 , , , < < ,则小亮同学骑车上学时,离家的路程s与所用时间t的函数关系图象可能是( ) A、
A、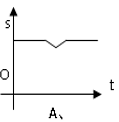 B、
B、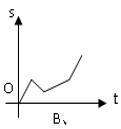 C、
C、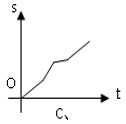 D、
D、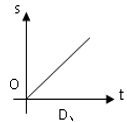
二、填空题(共6个题,每题3分,共18分)
-
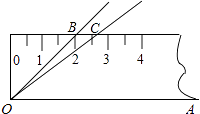
11. 分解因式:ba2+b+2ab= .12. 分式方程 的解是.13. 如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为 cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
 14. 如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集是
14. 如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集是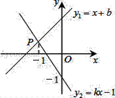 15. 如图,一辆小汽车在公路l上由东向西行驶,已知测速探头M到公路l的距离MN为9米,测得此车从点A行驶到点B所用的时间为0.6秒,并测得点A的俯角为30o , 点B的俯角为60o.那么此车从A到B的平均速度为米/秒.(结果保留三个有效数字,参考数据: ≈1.732, ≈1.414)
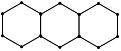
15. 如图,一辆小汽车在公路l上由东向西行驶,已知测速探头M到公路l的距离MN为9米,测得此车从点A行驶到点B所用的时间为0.6秒,并测得点A的俯角为30o , 点B的俯角为60o.那么此车从A到B的平均速度为米/秒.(结果保留三个有效数字,参考数据: ≈1.732, ≈1.414)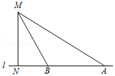 16. 如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍. 如果搭建正三角形和正六边形共用了2018根火柴棍,并且正三角形的个数比正六边形的个数多7个,那么能连续搭建正三角形的个数是;
16. 如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍. 如果搭建正三角形和正六边形共用了2018根火柴棍,并且正三角形的个数比正六边形的个数多7个,那么能连续搭建正三角形的个数是;

三、解答题
-
17. 计算:18. 先化简,后计算: ,其中19. 解不等式组: ,并在数轴上表示不等式组的解集.20. 已知关于 的方程 有两个不相等的实数根 、 .(1)、求 的取值范围;(2)、试说明 , ;(3)、若| |+| |=2| |-3,求k的值.21. 如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
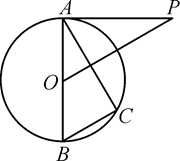 (1)、求证:PA为⊙O的切线;(2)、若OB=5,OP= ,求AC的长.22. 如图,在△ABC 中,BA=BC,以AB 为直径作半圆⊙O,交AC 于点D.连结DB,过点D 作DE⊥BC,垂足为点E.
(1)、求证:PA为⊙O的切线;(2)、若OB=5,OP= ,求AC的长.22. 如图,在△ABC 中,BA=BC,以AB 为直径作半圆⊙O,交AC 于点D.连结DB,过点D 作DE⊥BC,垂足为点E.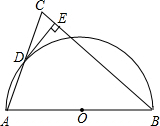 (1)、求证:DE 为⊙O 的切线;(2)、求证:DB2=AB·BE.23. 现要把228吨物资从某地运往甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如表:
(1)、求证:DE 为⊙O 的切线;(2)、求证:DB2=AB·BE.23. 现要把228吨物资从某地运往甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如表:运往地
车 型
甲 地(元/辆)
乙 地(元/辆)
大货车
720
800
小货车
500
650
(1)、求这两种货车各用多少辆?(2)、如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);(3)、在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.24. 抛物线y=x2+bx+c与x轴交于A(1,0),B(m,0),与y轴交于C.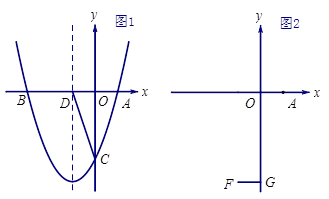 (1)、若m=-3,求抛物线的解析式,并写出抛物线的对称轴;(2)、如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在对称轴左侧的抛物线上有一点E,使S△ACE = S△ACD , 求E点的坐标;(3)、如图2,设F(-1,-4),FG⊥y轴于G,在线段OG上是否存在点P,使∠OBP=∠FPG?若存在,求m的取值范围;若不存在,请说明理由.
(1)、若m=-3,求抛物线的解析式,并写出抛物线的对称轴;(2)、如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在对称轴左侧的抛物线上有一点E,使S△ACE = S△ACD , 求E点的坐标;(3)、如图2,设F(-1,-4),FG⊥y轴于G,在线段OG上是否存在点P,使∠OBP=∠FPG?若存在,求m的取值范围;若不存在,请说明理由.