浙江省台州市2020年数学中考仿真模拟卷
试卷更新日期:2020-07-07 类型:中考模拟
一、一.选择题(共10小题,满分40分,每小题4分)
-
1. ﹣ 的相反数是( )A、2 B、﹣2 C、 D、±2. 为应对疫情,许多企业跨界抗疫,生产口罩.截至2月29日,全国口罩日产量达到116000000只.将116000000用科学记数法表示应为( )A、 B、 C、 D、3. 如图是由5个大小相同的立方体搭成的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、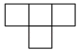 4. 甲乙两名同学本学期参加了相同的5次数学考试,老师想判断这两位同学的数学成绩谁更稳定,老师需比较这两人5次数学成绩的( )A、平均数 B、中位数 C、众数 D、方差5. 将一个矩形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )
4. 甲乙两名同学本学期参加了相同的5次数学考试,老师想判断这两位同学的数学成绩谁更稳定,老师需比较这两人5次数学成绩的( )A、平均数 B、中位数 C、众数 D、方差5. 将一个矩形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )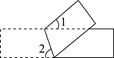 A、40° B、50° C、60° D、70°6. 面积为4的矩形的长为x,宽为y,则y与x的函数关系的图象大致是( )A、
A、40° B、50° C、60° D、70°6. 面积为4的矩形的长为x,宽为y,则y与x的函数关系的图象大致是( )A、 B、
B、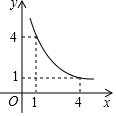 C、
C、 D、
D、 7. 下列计算正确的是( )A、(a﹣b)(﹣a﹣b)=a2﹣b2 B、2a3+3a3=5a5 C、6x3y2÷3x=2x2y2 D、(﹣2x2)3=﹣6x3y68. 如图是某商品标牌的示意图,⊙O与等边△ABC的边BC相切于点C,且⊙O的直径与△ABC的高相等,已知等边△ABC边长为4,设⊙O与AC相交于点E,则AE的长为( )
7. 下列计算正确的是( )A、(a﹣b)(﹣a﹣b)=a2﹣b2 B、2a3+3a3=5a5 C、6x3y2÷3x=2x2y2 D、(﹣2x2)3=﹣6x3y68. 如图是某商品标牌的示意图,⊙O与等边△ABC的边BC相切于点C,且⊙O的直径与△ABC的高相等,已知等边△ABC边长为4,设⊙O与AC相交于点E,则AE的长为( )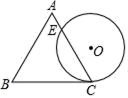 A、 B、1 C、 ﹣1 D、9. 如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( )
A、 B、1 C、 ﹣1 D、9. 如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( ) A、1个 B、2个 C、3个 D、4个10. 小明遇到这样一个问题:如图,矩形纸片ABCD,AB=2,BC=3,现要求将矩形纸片剪两刀后拼成一个与之面积相等的正方形,小明尝试给出了下面四种剪的方法,如图①②③④,图中BE= .
A、1个 B、2个 C、3个 D、4个10. 小明遇到这样一个问题:如图,矩形纸片ABCD,AB=2,BC=3,现要求将矩形纸片剪两刀后拼成一个与之面积相等的正方形,小明尝试给出了下面四种剪的方法,如图①②③④,图中BE= .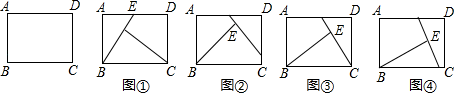
其中剪法正确的是( )
A、①② B、①③ C、②③ D、③④二、二.填空题(共6小题,满分30分,每小题5分)
-
11. 实数 的平方根是.12. 因式分解:x﹣x2= .13. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是 .14. 某种型号汽车每行驶100km耗油10L,其油箱容量为40L.为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的 ,按此建议,一辆加满油的该型号汽车最多行驶的路程是km.15. 一养鸡专业户计划用116m长的篱笆围成如图所示的三间长方形鸡舍,门MN宽2m,门PQ和RS的宽都是1m,围成的鸡舍面积最大是平方米.
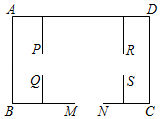 16. 如图,在直角坐标系中,A,B为定点,A(2,﹣3),B(4,﹣3),定直线l∥AB,P是l上一动点,l到AB的距离为6,M,N分别为PA,PB的中点下列说法中:
16. 如图,在直角坐标系中,A,B为定点,A(2,﹣3),B(4,﹣3),定直线l∥AB,P是l上一动点,l到AB的距离为6,M,N分别为PA,PB的中点下列说法中:①线段MN的长始终为1;②△PAB的周长固定不变;
③△PMN的面积固定不变; ④若存在点Q使得四边形APBQ是平行四边形,则Q到MN所在直线的距离必为9.
其中正确的说法是.

三、三.解答题(共8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80分)
-
17. 计算:(﹣1)2+(π﹣3.14)0﹣| ﹣2|
18. 先化简,再求值: ,其中a=2.19. 如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).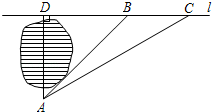 20. 如图,一次函数y=mx+2m+3的图象与y=﹣ x的图象交于点C,且点C的横坐标为﹣3,与x轴、y轴分别交于点A、点B.
20. 如图,一次函数y=mx+2m+3的图象与y=﹣ x的图象交于点C,且点C的横坐标为﹣3,与x轴、y轴分别交于点A、点B. (1)、求m的值与AB的长;(2)、若点Q为线段OB上一点,且 S△OCQ= S△BAO , 求点Q的坐标.21. 为了解家长对“学生在校带手机”现象的看法,某校“九年级兴趣小组”随机调查了该校学生家长若干名,并对调查结果进行整理,绘制如下不完整的统计图.
(1)、求m的值与AB的长;(2)、若点Q为线段OB上一点,且 S△OCQ= S△BAO , 求点Q的坐标.21. 为了解家长对“学生在校带手机”现象的看法,某校“九年级兴趣小组”随机调查了该校学生家长若干名,并对调查结果进行整理,绘制如下不完整的统计图.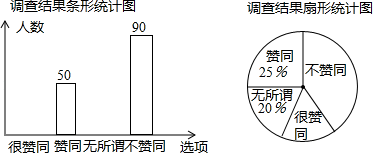
根据以上信息,解答下列问题:
(1)、这次接受调查的家长总人数为人.(2)、在扇形统计图中,求“很赞同”所对应的扇形圆心角的度数;(3)、若在这次接受调查的家长中,随机抽出一名家长,恰好抽到“无所谓”的家长概率是多少?22. 如图,已知等腰直角三角形ABC,点D是斜边AC上一点(不与A、C重合),DE是△BCD的外接圆⊙O的直径.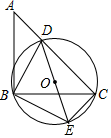 (1)、求证:△BDE是等腰直角三角形;(2)、若⊙O的直径为5,求AD2+CD2的值.23. 已知点A (1,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)上一点.(1)、用a的代数式表示b;(2)、若1≤a≤2,求﹣ 的范围;(3)、在(2)的条件下,设当1≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n(用a的代数式表示).24. 如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转90°得到线段PE,连接AE,BP,CE.
(1)、求证:△BDE是等腰直角三角形;(2)、若⊙O的直径为5,求AD2+CD2的值.23. 已知点A (1,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)上一点.(1)、用a的代数式表示b;(2)、若1≤a≤2,求﹣ 的范围;(3)、在(2)的条件下,设当1≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n(用a的代数式表示).24. 如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转90°得到线段PE,连接AE,BP,CE. (1)、求证:△APE∽△ABC;(2)、当线段BP与CE相交时,设交点为M,求 的值以及∠BMC的度数;(3)、若正方形ABCD的边长为3,AP=1,当点P,C,E在同一直线上时,求线段BP的长.
(1)、求证:△APE∽△ABC;(2)、当线段BP与CE相交时,设交点为M,求 的值以及∠BMC的度数;(3)、若正方形ABCD的边长为3,AP=1,当点P,C,E在同一直线上时,求线段BP的长.