浙江省杭州市2020年数学中考仿真模拟卷
试卷更新日期：2020-07-07 类型：中考模拟
一、一.选择题（本大题有10个小题，每小题3分，共30分.）
-
1. ﹣9的绝对值是（ ）A、﹣9 B、9 C、 D、2. 截止到3月26日0时，全球感染新型冠状病毒肺炎的人数已经突破380000人，“山川异域，风月同天”，携手抗“疫”，刻不容缓.将380000用科学记数法表示为（ ）A、0.38×106 B、3.8×105 C、38×104 D、3.8×1063. 如图，AB、AC、BD是⊙O的切线，切点分别是P、C、D.若AB＝5，AC＝3，则BD的长是（ ）
A、4 B、3 C、2 D、14. 下列各式运用等式的性质变形，错误的是（ ）A、若﹣a＝﹣b，则a＝b B、若 ＝ ，则a＝b C、若ac＝bc，则a＝b D、若（m2+1）a＝（m2+1）b，则a＝b5. 如图，在△ABC中，D为AB中点，DE∥BC交AC于E点，则△ADE与△ABC的面积比为（ ）
A、1：1 B、1：2 C、1：3 D、1：46. 某公园门票的价格为：成人票10元/张，儿童票5元/张.现有x名成人、y名儿童，买门票共花了75元.据此可列出关于x、y的二元一次方程为（ ）A、10x+5y＝75 B、5x+10y＝75 C、10x﹣5y＝75 D、10x＝75+5y7. 一个不透明的布袋里装有3个红球，2个黑球，若干个白球；从布袋中随机摸出一个球，摸出的球是红球的概率是 ，袋中白球共有（ ）A、1个 B、2个 C、3个 D、4个8. 如图，在Rt△ABC中，∠ABC＝90°，AB＝2，BC＝1.把△ABC分别绕直线AB和BC旋转一周，所得几何体的底面圆的周长分别记作l1 ， l2 ， 侧面积分别记作S1 ， S2 ， 则（ ）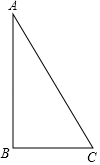
A、l1：l2＝1：2，S1：S2＝1：2 B、l1：l2＝1：4，S1：S2＝1：2 C、l1：l2＝1：2，S1：S2＝1：4 D、l1：l2＝1：4，S1：S2＝1：49. 二次函数y＝2x2+bx+c的图象如图所示，点A，点B是图象与x轴的两个交点，若AB＝2 ，则二次函数y＝2x2+bx+c的最小值是（ ）
A、﹣6 B、﹣4 C、﹣4 D、﹣610. 如图，在△ABC中，过点A作射线AD∥BC，点D不与点A重合，且AD≠BC，连结BD交AC于点O，连结CD，设△ABO、△ADO、△CDO和△BCO的面积分别为S1、S2、S3和S4 ， 则下列说法不正确的是（ ）
A、S1＝S3 B、S1+S2＝S3+S2 C、S1+S4＝S3+S4 D、S1+S2＝S3+S4二、二.填空题（本大题有6个小题，每小题4分，共24分）
-
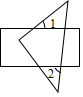
11. 某次数学测验中，五位同学的分数分别是89，91，105，105，110，这组数据的中位数是.12. 因式分解：m2﹣9＝.13. 将一个含有45°角的直角三角板摆放在矩形上，如图所示，若∠1＝40°，则∠2＝ ．
14. 请写出一个图象经过点（1，2），且第一象限内的函数值随着自变量的值增大而减小的函数表达式：.15. 如图，AB，CD是⊙O的弦，且AB⊥CD，连接AD，BC，若∠C＝25°，则∠D的度数为.
16. 如图，将一张长方形纸片ABCD沿AC折起，重叠部分为△ACE，若AB＝6，BC＝4，则重叠部分△ACE的面积为.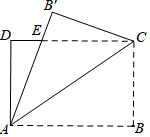
三、三.解答题（本小题7个小题，共66分）
-
17. 你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y（m）是面条的粗细（横截面积）S（mm2）的反比例函数，其图象如图所示.
(1)、写出y（m）与S（mm2）的函数关系式；(2)、求当面条粗2mm2时，面条的总长度是多少米？18. 某校组织八年级学生参加汉字听写大赛，并随机抽取部分学生成绩作为样本进行分析，绘制成如下的统计表：成绩x/分
频数
频率
x＜60
2
0.04
60≤x＜70
6
0.12
70≤x＜80
9
b
80≤x＜90
a
0.36
90≤x≤100
15
0.30
请根据所给信息，解答下列问题
(1)、a＝ ， b＝(2)、请补全频数分布直方图；(3)、若得分不低于80分的成绩为“优秀”，则这次抽取成绩为“优秀”所占抽取人数的百分比是多少？19. 如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF＝∠GAC.
(1)、求证：△ADE∽△ABC；(2)、若AD＝3，AB＝5，求 的值．20. 设一次函数y＝kx+b（k，b是常数，k≠0）的图象过A（1，3），B（﹣1，﹣1）两点.(1)、求该一次函数的表达式；(2)、若点（2a+2，a2）在该一次函数图象上，求a的值.(3)、已知点C（x1 ， y1）和点D（x2 ， y2）在该一次函数图象上，设m＝（x1﹣x2）（y1﹣y2），判断反比例函数y＝ 的图象所在的象限，说明理由.21. 如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC于点E，GF⊥BC于点F，连结AG.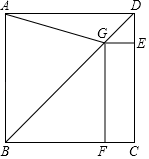
(1)、写出线段AG，GE，GF长度之间的数量关系，并说明理由；(2)、若正方形ABCD的边长为1，∠AGF＝105°，求线段BG的长.22. 如图，抛物线y＝ax2+ x+c（a≠0）与x轴交于点A，B两点，其中A（﹣1，0），与y轴交于点C（0，2）．
(1)、求抛物线的表达式及点B坐标；(2)、点E是线段BC上的任意一点（点E与B、C不重合），过点E作平行于y轴的直线交抛物线于点F，交x轴于点G．①设点E的横坐标为m，用含有m的代数式表示线段EF的长；
②线段EF长的最大值是 ．
23. 定义：如果一个三角形中有两个内角α，β满足α+2β＝90°，那我们称这个三角形为“近直角三角形”.
(1)、若△ABC是“近直角三角形”，∠B＞90°，∠C＝50°，则∠A＝度；(2)、如图1，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4.若BD是∠ABC的平分线，①求证：△BDC是“近直角三角形”；
②在边AC上是否存在点E（异于点D），使得△BCE也是“近直角三角形”？若存在，请求出CE的长；若不存在，请说明理由.
(3)、如图2，在Rt△ABC中，∠BAC＝90°，点D为AC边上一点，以BD为直径的圆交BC于点E，连结AE交BD于点F，若△BCD为“近直角三角形”，且AB＝5，AF＝3，求tan∠C的值.