广东省潮州市2019-2020学年高一下学期数学期中考试试卷
试卷更新日期:2020-07-07 类型:期中考试
一、单选题
-
1. 若函数 的图象经过定点P,且点 在角 的终边上,则 的值等于( )A、2 B、 C、-2 D、2. 已知倾斜角为 的直线 与直线 垂直,则 的值为( )A、 B、 C、-2 D、3. 已知 =(2,3), =(3,t), =1,则 =( )A、-3 B、-2 C、2 D、34. 已知sin θ+cos θ= ,θ∈ ,则sin θ-cos θ的值为( )A、- B、 C、 D、-5. 下列函数中,以 为周期且在区间( , )单调递增的是( )A、f(x)=│cos2x│ B、f(x)=│sin 2x│ C、f(x)=cos│x│ D、f(x)= sin│x│6. 已知函数 是奇函数,将 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 .若 的最小正周期为 ,且 ,则 ( )A、-2 B、 C、 D、27. 在 中,点 在线段 上,且 ,点O在线段 上(与点C,D不重合)若 ,则x的取值范围是( )A、 B、 C、 D、8. 函数y= sin2x的图象可能是( )
A、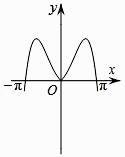 B、
B、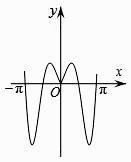 C、
C、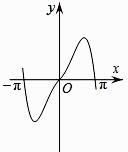 D、
D、 9. 已知 , , , ,则 的取值范围是( )A、 B、[0,2] C、 D、[0,1]10. 在 中, , , , 在边 的中线 上,则 的最小值为( )A、 B、0 C、4 D、-111. 已知函数 ,则 的所有零点之和等于( )A、8π B、7π C、6π D、5π12. 已知A,B,C,D是函数 一个周期内的图象上的四个点,如图所示, ,B为y轴上的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称, 在x轴上的投影为 ,则ω,φ的值为( )
9. 已知 , , , ,则 的取值范围是( )A、 B、[0,2] C、 D、[0,1]10. 在 中, , , , 在边 的中线 上,则 的最小值为( )A、 B、0 C、4 D、-111. 已知函数 ,则 的所有零点之和等于( )A、8π B、7π C、6π D、5π12. 已知A,B,C,D是函数 一个周期内的图象上的四个点,如图所示, ,B为y轴上的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称, 在x轴上的投影为 ,则ω,φ的值为( ) A、ω=2,φ= B、ω=2,φ= C、ω= ,φ= D、ω= ,φ=
A、ω=2,φ= B、ω=2,φ= C、ω= ,φ= D、ω= ,φ=二、填空题
-
13. 设向量 , , ,若 ,则 .14. 已知函数 , .若不等式 在 上恒成立,则实数m的取值范围为.15. 设函数 ( 是常数, ).若 在区间 上具有单调性,且 ,则 的最小正周期为.16. 已知函数 ,记函数 在区间 上的最大值为M,最小值为m,设函数 .若 ,则函数 的值域为.
三、解答题
-
17. 某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入了部分数据,如下表:
0
0
5
-5
0
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数 的解析式;
(Ⅱ)将 图象上所有点向左平行移动 个单位长度,得到 的图象.若 图象的一个对称中心为 ,求 的最小值.
18.(1)、已知 ,求 的值.(2)、在三角形 中,点P是 上一点,且 ,Q是 的中点, 与 的交点为M,又 ,求实数t的值.19. 已知向量 , (m是常数),且 .(1)、若 是奇函数,求m的值;(2)、设函数 ,讨论当实数m变化时,函数 的零点个数.20. 在平面直角坐标系中, 为坐标原点,已知向量 , , .(1)、若 ,且 ,求向量 的坐标.(2)、若 ,求 的最小值.