高中数学人教新课标A版必修一 1.2.2函数的表示法
试卷更新日期:2020-07-06 类型:同步测试
一、单选题
-
1. 下列四个图象中,是函数图象的是( )
 A、① B、①③④ C、①②③ D、③④2. 国内快递1 000 g以内的包裹的邮资标准如表:
A、① B、①③④ C、①②③ D、③④2. 国内快递1 000 g以内的包裹的邮资标准如表:运送距离x(km)
0<x
≤500
500<x
≤1 000
1 000<x
≤1 500
…
邮资y(元)
5.00
6.00
7.00
…
如果某人在西安要邮寄800 g的包裹到距西安1 200 km的某地,那么他应付的邮资是( )
A、5.00元 B、6.00元 C、7.00元 D、无法确定3. 是一次函数,且 ,则 ( )A、 B、
B、 C、
C、 D、
D、 4. 设函数 ,则 的表达式是( )A、 B、 C、 D、5. 已知函数 ,部分x与y的对应关系如表:
4. 设函数 ,则 的表达式是( )A、 B、 C、 D、5. 已知函数 ,部分x与y的对应关系如表:x
0
1
2
3
4
y
3
2
1
0
0
则
A、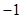 B、
B、 C、
C、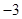 D、3
6. 已知 是一次函数,且满足 ,则 ( ).A、 B、 C、 D、7. 设 , ,下列图形能表示从集合A到集合B的函数图象的是( )A、
D、3
6. 已知 是一次函数,且满足 ,则 ( ).A、 B、 C、 D、7. 设 , ,下列图形能表示从集合A到集合B的函数图象的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知函数 ,则函数 的解析式为( )A、 B、 C、 D、9. 已知函数 满足 ,则 的解析式为( )A、 B、 C、 D、10. 设f,g都是由A到A的映射,其对应法则如下:
8. 已知函数 ,则函数 的解析式为( )A、 B、 C、 D、9. 已知函数 满足 ,则 的解析式为( )A、 B、 C、 D、10. 设f,g都是由A到A的映射,其对应法则如下:映射f的对应法则
x
1
2
3
4
f(x)
3
4
2
1
映射g的对应法则
x
1
2
3
4
g(x)
4
3
1
2
则f[g(1)]的值为( )
A、1 B、2 C、3 D、411. 若函数 满足 ,则 的解析式为( )A、 B、 C、 D、12. 国家相继出台多项政策控制房地产行业,现在规定房地产行业收入税如下:年收入在280万元及以下的税率为 ;超过280万元的部分按 征税.现有一家公司的实际缴税比例为 ,则该公司的年收入是( )A、 万元 B、 万元 C、 万元 D、 万元13. 已知函数f(x+1)=x2+2x,则f(x)的解析式为( )A、f(x)=x2+1 B、f(x)=x2+2x-1 C、f(x)=x2-1 D、f(x)=x2+2x+114. 已知 ,则 的解析式是( )A、 B、 C、 D、