江西省九江市2020届高三理数第三次模拟考试试卷

试卷更新日期：2020-07-06 类型：高考模拟

进入出卷网下载

一、单选题

1. 复数 $z = \frac{- 1 + i}{2 + i}$ 的虚部为（）

A、 $- \frac{3}{5} i$ B、 $- \frac{3}{5}$ C、 $\frac{3}{5} i$ D、 $\frac{3}{5}$

查看试题解析
2. 若集合 $A = {x | l o g_{2} (x - 1) < 2} ， B = {x | x^{2} - 2 x - 8 \leq 0}$ ，则A∪B＝（）

A、{x|x＜5} B、{x|﹣2≤x≤4} C、{x|﹣2≤x＜5} D、{x|1＜x≤4}

查看试题解析
3. 若数列{a_n}为等比数列，则“a₂ ， a₄是方程x²﹣3x+1＝0的两根”是“a₃＝±1”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 抛物线y＝ax²上一点 $P (- \frac{1}{4} ， \frac{1}{8})$ 到其准线的距离为（）

A、 $\frac{3}{4}$ B、 $\frac{1}{4}$ C、 $\frac{1}{8}$ D、 $\frac{3}{8}$

查看试题解析
5. 若a，b为正实数，直线 $2 x + (2 a - 3) y + 2 = 0$ 与直线 $b x + 2 y - 1 = 0$ 互相垂直，则 $a b$ 的最大值为（）

A、 $\frac{3}{2}$ B、 $\frac{9}{8}$ C、 $\frac{9}{4}$ D、 $\frac{3 \sqrt{2}}{4}$

查看试题解析
6. 如图是九江市2019年4月至2020年3月每月最低气温与最高气温（℃）的折线统计图：已知每月最低气温与最高气温的线性相关系数r＝0.83，则下列结论错误的是（）

A、每月最低气温与最高气温有较强的线性相关性，且二者为线性正相关 B、月温差（月最高气温﹣月最低气温）的最大值出现在10月 C、9﹣12月的月温差相对于5﹣8月，波动性更大 D、每月最高气温与最低气温的平均值在前6个月逐月增加

查看试题解析
7. 2019年11月26日，联合国教科文组织宣布3月14日为“国际数学日”（昵称： $π d a y$ ），2020年3月14日是第一个“国际数学日”．圆周率 $π$ 是圆的周长与直径的比值，是一个在数学及物理学中普遍存在的数学常数． $π$ 有许多奇妙性质，如莱布尼兹恒等式 $\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \dots = \frac{π}{4}$ ，即为正奇数倒数正负交错相加等于 $\frac{π}{4}$ ．小红设计了如图所示的程序框图，要求输出的T值与 $π$ 非常近似，则①、②中分别填入的可以是（）

A、 $S = {(- 1)}^{i - 1} \frac{1}{i}$ ， $i = i + 2$ B、 $S = {(- 1)}^{i - 1} \frac{1}{2 i - 1}$ ， $i = i + 1$ C、 $S = S + {(- 1)}^{i - 1} \frac{1}{i}$ ， $i = i + 2$ D、 $S = S + {(- 1)}^{i - 1} \frac{1}{2 i - 1}$ ， $i = i + 1$

查看试题解析
8. 在一个不透明的盒子中装有4个大小、形状、手感完全相同的小球，分别标有数字1，2，3，4．现每次有放回地从中任意取出一个小球，直到标有偶数的球都取到过就停止．小明用随机模拟的方法估计恰好在第4次停止摸球的概率，利用计算机软件产生随机数，每1组中有4个数字，分别表示每次摸球的结果，经随机模拟产生了以下21组随机数：由此可以估计恰好在第4次停止摸球的概率为（）
1314 1234 2333 1224 3322 1413 3124 4321 2341 2413 1224 2143 4312

2412 1413 4331 2234 4422 3241 4331 4234

A、 $\frac{2}{7}$ B、 $\frac{1}{3}$ C、 $\frac{8}{21}$ D、 $\frac{5}{21}$

查看试题解析
9. 函数 $f (x) = e^{| x |} - x \sin x - 1$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
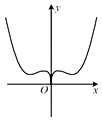10. 设双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为F₁ ， F₂ ，过点F₂的直线分别交双曲线左、右两支于点P，Q，点M为线段PQ的中点，若P，Q，F₁都在以M为圆心的圆上，且 $\vec{P Q} \cdot \vec{M F_{1}} = 0$ ，则双曲线C的离心率为（）

A、 $\sqrt{2}$ B、2 $\sqrt{2}$ C、 $\sqrt{3}$ D、2 $\sqrt{3}$

查看试题解析
11. 如图所示，三棱锥S一ABC中，△ABC与△SBC都是边长为1的正三角形，二面角A﹣BC﹣S的大小为 $\frac{2 π}{3}$ ，若S，A，B，C四点都在球O的表面上，则球O的表面积为（）

A、 $\frac{7}{3}$ π B、 $\frac{13}{3}$ π C、 $\frac{4}{3}$ π D、3π

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} - 2 x^{2} - 4 x - 1 ， x \leq 0 \\ x^{3} - 3 x^{2} + 3 ， x > 0 \end{array}$ ，若不等式 $\frac{f (x) - m}{x} \leq 0 (m \in Z)$ 恰有两个整数解，则m的个数为（）

A、6 B、7 C、8 D、9

查看试题解析

二、填空题

13. 已知向量 $\vec{a} = (2 ， 1) ， \vec{b} = (- 1 ， x)$ ，若 $\vec{a} + \vec{b}$ 与 $\vec{a} - \vec{b}$ 共线，则实数x的值为．

查看试题解析
14. 若二项式 ${(x + \frac{3}{x})}^{n}$ 的展开式中各项系数和为256，则展开式中的常数项为．

查看试题解析
15. 设等差数列{a_n}满足：a₁＝3，公差d∈（0，10），其前n项和为S_n ．若数列 ${\sqrt{S_{n} + 1}}$ 也是等差数列，则 $\frac{S_{n} + 10}{a_{n} + 1}$ 的最小值为．

查看试题解析
16. 在棱长为1的正方体ABCD﹣A₁B₁C₁D₁中，点M，N分别是棱B₁C₁ ， C₁D₁的中点，过A，M，N三点作正方体的截面，将截面多边形向平面ADD₁A₁作投影，则投影图形的面积为．

查看试题解析

三、解答题

17. 在△ABC中，三内角A，B，C满足 $1 - s i n A s i n B = s i n^{2} \frac{C}{2}$ ．

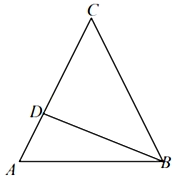
（Ⅰ）判断△ABC的形状；

（Ⅱ）若点D在线段AC上，且CD＝2DA， $t a n ∠ A B D = \frac{2}{5}$ ，求tanA的值．

查看试题解析
18. 已知正△ABC边长为3，点M，N分别是AB，AC边上的点，AN＝BM＝1，如图1所示．将△AMN沿MN折起到△PMN的位置，使线段PC长为 $\sqrt{5}$ ，连接PB，如图2所示．

（Ⅰ）求证：平面PMN⊥平面BCNM；

（Ⅱ）若点D在线段BC上，且BD＝2DC，求二面角M﹣PD﹣C的余弦值．

查看试题解析
19. 如图所示，在平面直角坐标系 $x O y$ 中，已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{6}}{3}$ ，A为椭圆E上位于第一象限上的点， $B$ 为椭圆E的上顶点，直线 $A B$ 与x轴相交于点C， $| A B | = | A O |$ ， $△ B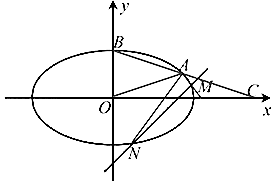 O C$ 的面积为6．

（Ⅰ）求椭圆E的标准方程；

（Ⅱ）设直线l过椭圆E的右焦点，且与椭圆E相交于M、N两点（M、N在直线 $O A$ 的同侧），若 $∠ C A M = ∠ O A N$ ，求直线l的方程.

查看试题解析
20. 已知函数 $f (x) = a (\ln x - 1) + \frac{1}{x} (a \in R)$ ，存在极小值点 $x_{0}, f (x_{0}) < 0$ ．
（Ⅰ）求a的取值范围；

（Ⅱ）设 $m, n > 0$ ，且 $m \neq n$ ，求证： $\frac{f (m) - f (n)}{m - n} > \frac{1}{m + n} - \frac{1}{m n}$ ．

查看试题解析
21. 为筛查在人群中传染的某种病毒，现有两种检测方法：
⑴抗体检测法：每个个体独立检测，每一次检测成本为80元，每个个体收取检测费为100元．

⑵核酸检测法：先合并个体，其操作方法是：当个体不超过10个时，把所有个体合并在一起进行检测．

当个体超过10个时，每10个个体为一组进行检测．若该组检测结果为阴性（正常），则只需检测一次；若该组检测结果为阳性（不正常），则需再对每个个体按核酸检测法重新独立检测，共需检测k+1次（k为该组个体数，1≤k≤10，k∈N^*）．每一次检测成本为160元．假设在接受检测的个体中，每个个体的检测结果是阳性还是阴性相互独立，且每个个体是阳性结果的概率均为p（0＜p＜1）．

（Ⅰ）现有100个个体采取抗体检测法，求其中恰有一个检测出为阳性的概率；

（Ⅱ）因大多数人群筛查出现阳性的概率很低，且政府就核酸检测法给子检测机构一定的补贴，故检测机构推出组团选择核酸检测优惠政策如下：无论是检测一次还是k+1次，每组所有个体共收费700元（少于10个个体的组收费金额不变）．已知某企业现有员工107人，准备进行全员检测，拟准备9000元检测费，由于时间和设备条件的限制，采用核酸检测法合并个体的组数不得高于参加采用抗体检测法人数，请设计一个合理的的检测安排方案；

（Ⅲ）设 $p = 1 - e^{- \frac{1}{24}}$ ，现有n（n∈N^*且2≤n≤10）个个体，若出于成本考虑，仅采用一种检测方法，试问检测机构应采用哪种检测方法？（ln3≈1.099，ln4≈1.386，ln5≈1.609，ln6≈1.792）

查看试题解析
22. 在平面直角坐标系xOy中，曲线C的参数方程为 ${\begin{array}{l} x = \frac{1}{2} (t + \frac{1}{t}) \\ y = t - \frac{1}{t} \end{array}$ （t为参数），以原点O为极点，x轴的非负半轴为极轴建立极坐标系．
（Ⅰ）写出曲线C的普通方程和极坐标方程；

（Ⅱ）M，N为曲线C．上两点，若OM⊥ON，求|MN|的最小值．

查看试题解析
23. 定义区间 $(x_{1}, x_{2})$ $(x_{2} > x_{1})$ 的长度为 $x_{2} - x_{1}$ ，已知不等式 $| x - m | \cdot | x - 1 | + 1 < x$ $(m \in R)$ 的解集区间长度为1．
（Ⅰ）求m的值；

（Ⅱ）若 $a, b \in R$ ， $a b > 0$ ， $a + b = m$ ，求 $\frac{b^{2}}{a} + \frac{a^{2}}{b}$ 的最小值及此时a，b的值．

查看试题解析