江西省2019-2020学年高三理数质量监测试卷

试卷更新日期：2020-07-06 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知 $(1 + i) z = i$ （i为虚数单位），在复平面内，复数z的共扼复数 $\bar{z}$ 对应的点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 全集 $U = R$ ，集合 $A = {x | \frac{x}{x - 4} \leq 0}$ ，集合 $B = {x | \log_{2} (x - 1) > 2}$ ，图中阴影部分所表示的集合为（）

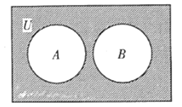A、 $(- \infty ， 0] \cup [4 ， 5]$ B、 $(- \infty ， 0) \cup (4 ， 5]$ C、 $(- \infty ， 0) \cup [4 ， 5]$ D、 $(- \infty ， 4] \cup (5 ， + \infty)$

查看试题解析
3. 已知抛物线 $a x^{2} = y$ 的焦点到准线的距离为 $\frac{1}{2}$ ，则实数a等于（）

A、±1 B、±2 C、 $\pm \frac{1}{4}$ D、 $\pm \frac{1}{2}$

查看试题解析
4. 已知 ${a_{n}}$ 是等比数列， $a_{1} > 0$ ，前n项和为 $S_{n}$ ，则“ $2 S_{8} < S_{7} + S_{9}$ ”是“ ${a_{n}}$ 为递增数列”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 千百年来，我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化，总结了丰富的“看云识天气”的经验，并将这些经验编成谚语，如“天上钩钩云，地上雨淋淋”“日落云里走，雨在半夜后”……小波同学为了验证“日落云里走，雨在半夜后”，观察了所在地区A的100天日落和夜晚天气，得到如下 $2 \times 2$ 列联表：

夜晚天气

日落云里走

下雨

未下雨

出现

25

5

未出现

25

45

临界值表

P（ $K^{2} \geq k_{0}$ ）

0.10

0.05

0.010

0.001

$k_{0}$

2.706

3.841

6.635

10.828

并计算得到 $K^{2} \approx 19.05$ ，下列小波对地区A天气判断不正确的是（）

A、夜晚下雨的概率约为 $\frac{1}{2}$ B、未出现“日落云里走”夜晚下雨的概率约为 $\frac{5}{14}$ C、有 $99.9 %$ 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关 D、出现“日落云里走”，有 $99.9 %$ 的把握认为夜晚会下雨

查看试题解析
6. 圆C的半径为5，圆心在x轴的负半轴上，且被直线 $3 x + 4 y + 4 = 0$ 截得的弦长为6，则圆C的方程为（）

A、 $x^{2} + y^{2} - 2 x - 3 = 0$ B、 $x^{2} + 16 x + y^{2} + 39 = 0$ C、 $x^{2} - 16 x + y^{2} - 39 = 0$ D、 $x^{2} + y^{2} - 4 x = 0$

查看试题解析
7. $2^{\frac{1}{3}}$ ， $\log_{2} 6$ ， $3 \log_{3} 2$ 的大小关系是（）

A、 $2^{\frac{1}{3}} < \log_{2} 6 < 3 \log_{3} 2$ B、 $2^{\frac{1}{3}} < 3 \log_{3} 2 < \log_{2} 6$ C、 $3 \log_{3} 2 < 2^{\frac{1}{3}} < \log_{2} 6$ D、 $3 \log_{3} 2 < \log_{2} 6 < 2^{\frac{1}{3}}$

查看试题解析
8. 在三角形 $A B C$ 中， $A B = 8$ ， $A C = 4$ ， $∠ B A C = 60 °$ ，双曲线以A、B为焦点，且经过点C，则该双曲线的离心率为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{2} + 1$ D、 $\sqrt{3} + 1$

查看试题解析
9. 已知函数 $f (x) = {\begin{array}{l} \lg x ， x \geq 1 \\ - \lg (2 - x) ， x < 1 \end{array}$ ， $g (x) = x^{3}$ ，则方程 $f (x) = g (x - 1)$ 所有根的和等于（）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图所示，直线 $l_{1} // l_{2}$ ，点A是 $l_{1}$ 、 $l_{2}$ 之间的一定点，并且点A到 $l_{1}$ 、 $l_{2}$ 的距离分别为2、4，过点A且夹角为 $\frac{π}{3}$ 的两条射线分别与 $l_{1}$ 、 $l_{2}$ 相交于B、C两点，则 $△ A B C$ 面积的最小值是（）

A、 $4 \sqrt{3}$ B、 $6 \sqrt{3}$ C、 $8 \sqrt{3}$ D、 $12 \sqrt{3}$

查看试题解析
11. 在三棱锥 $P - A B C$ 中，底面 $A B C$ 为正三角形， $P C ⊥ A C$ ， $P A = P B$ ，且 $P C + A C = 4$ .若三棱锥 $P - A B C$ 的每个顶点都在球O的球面上，则球O的半径的最小值为（）

A、 $\frac{\sqrt{7}}{7}$ B、 $\frac{2 \sqrt{7}}{7}$ C、 $\frac{3 \sqrt{7}}{7}$ D、 $\frac{4 \sqrt{7}}{7}$

查看试题解析
12. 设 $f (x)$ 是在 $(0 ， + \infty)$ 上的可导函数，且 $f^{'} (x) \geq \frac{2}{x} f (x)$ ， $f (1) = 4$ ， $f (2) = 16$ ，则下列一定不成立的是（）

A、 $f (\frac{3}{2}) = 8$ B、 $f (3) = 40$ C、 $f (4) = 72$ D、 $f (5) = 120$

查看试题解析

二、填空题

13. ${(2 x^{2} + x - 1)}^{5}$ 的展开式中x的系数是.

查看试题解析
14. 设向量 $\vec{a} = (2 \cos θ, \sin θ)$ ，向量 $\vec{b} = (1, - 6)$ ，且 $\vec{a} \cdot \vec{b} = 0$ ，则 $\frac{2 \cos θ + 3 \sin θ}{\cos θ + 3 \sin θ}$ 等于.

查看试题解析
15. 已知一个四棱柱的三视图如图（图中小正方形的边长为1），则该四棱柱的全面积等于.

查看试题解析
16. 已知数列 ${a_{n}}$ 的通项公式是 $a_{n} = 2^{n}$ ，在 $a_{1}$ 和 $a_{2}$ 之间插入1个数 $x_{11}$ ，使 $a_{1}$ ， $x_{11}$ ， $a_{2}$ 成等差数列；在 $a_{2}$ 和 $a_{3}$ 之间插入2个数 $x_{21}$ ， $x_{22}$ ，使 $a_{2}$ ， $x_{21}$ ， $x_{22}$ ， $a_{3}$ 成等差数列；…；在 $a_{n}$ 和 $a_{n + 1}$ 之间插入n个数 $x_{n 1}$ ， $x_{n 2}$ ，…， $x_{n n}$ ，使 $a_{n}$ ， $x_{n 1}$ ， $x_{n 2}$ ，…， $x_{n n}$ ， $a_{n + 1}$ 成等差数列.这样得到新数列 ${b_{n}}$ ： $a_{1}$ ， $x_{11}$ ， $a_{2}$ ， $x_{21}$ ， $x_{22}$ ， $a_{3}$ ， $x_{31}$ ， $x_{32}$ ， $x_{33}$ ， $a_{4}$ ，….记数列 ${b_{n}}$ 的前n项和为 $S_{n}$ ，有下列判断：① $x_{n 1} + x_{n 2} + \dots + x_{n n} = 3 n \cdot 2^{n - 1}$ ；② $a_{10} = b_{66}$ ；③ $b_{72} = 3072$ ；④ $S_{55} = 14337$ .其中正确的判断序号是.

查看试题解析

三、解答题

17. 已知点O是 $△ A B C$ 的外接圆的圆心， $A B = 3$ ， $A C = 2 \sqrt{2}$ ， $∠ B A C = \frac{π}{4}$ .

(1)、求外接圆O的面积.

(2)、求 $\vec{B O} \cdot \vec{B C}$

查看试题解析
18. 如图所示，已知四边形 $A B C D$ 是菱形，平面 $A E F C ⊥$ 平面 $A B C D$ ， $E F // A C$ ， $A E = A B = A C = 2 E F = 2$ .

(1)、求证：平面 $B E D ⊥$ 平面 $A E F C$ .

(2)、若 $E A ⊥ A C$ ，求二面角 $B - F D - C$ 的余弦值.

查看试题解析

19. 2020年春节期间，全国人民都在抗击“新型冠状病毒肺炎”的斗争中.当时武汉多家医院的医用防护物资库存不足，某医院甚至面临断货危机，南昌某生产商现有一批库存的医用防护物资，得知消息后，立即决定无偿捐赠这批医用防护物资，需要用A、B两辆汽车把物资从南昌紧急运至武汉.已知从南昌到武汉有两条合适路线选择，且选择两条路线所用的时间互不影响.据调查统计2000辆汽车，通过这两条路线从南昌到武汉所用时间的频数分布表如下：

所用的时间（单位：小时）	$(3, 4]$	$(4, 5]$	$(5, 6]$	$(6, 7]$
路线1的频数	200	400	200	200
路线2的频数	100	400	400	100

假设汽车A只能在约定交货时间的前5小时出发，汽车B只能在约定交货时间的前6小时出发（将频率视为概率）.为最大可能在约定时间送达这批物资，来确定这两车的路线.

(1)、汽车A和汽车B应如何选择各自的路线.

(2)、若路线1、路线2的“一次性费用”分别为3.2万元、1.6万元，且每车医用物资生产成本为40万元（其他费用忽略不计），以上费用均由生产商承担，作为援助金额的一部分.根据这两辆车到达时间分别计分，具体规则如下（已知两辆车到达时间相互独立，互不影响）：

到达时间与约定时间的差x（单位：小时）	$x \leq 0$	$0 < x \leq 1$	$x > 1$
该车得分	0	1	2

生产商准备根据运输车得分情况给出现金排款，两车得分和为0，捐款40万元，两车得分和每增加1分，捐款增加20万元，若汽车A、B用（1）中所选的路线运输物资，记该生产商在此次援助活动中援助总额为Y（万元），求随机变量Y的期望值，（援助总额 $=$ 一次性费用 $+$ 生产成本 $+$ 现金捐款总额）

查看试题解析

20. 已知离心率为 $\frac{\sqrt{2}}{2}$ 的椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左顶点为A，左焦点为F，及点 $P (- 4, 0)$ ，且 $| O F |$ 、 $| O A |$ 、 $| O P |$ 成等比数列．

(1)、求椭圆C的方程；

(2)、斜率不为0的动直线l过点P且与椭圆C相交于M、N两点，记 $\vec{P M} = λ \vec{P N}$ ，线段 $M N$ 上的点A满足 $\vec{M Q} = λ \vec{Q N}$ ，试求 $△ O P Q$ （O为坐标原点）面积的取值范围．

查看试题解析
21. 已知函数 $f (x) = a x e^{x} + b$ （其中e是自然对数的底数，a， $b \in R$ ）在点 $(1 ， f (1))$ 处的切线方程是 $2 e x - y - e = 0$ .

(1)、求函数 $f (x)$ 的单调区间.

(2)、设函数 $g (x) = \frac{{[f (x)]}^{2}}{x} - m x - \ln x$ ，若 $g (x) \geq 1$ 在 $x \in (0 ， + \infty)$ 上恒成立，求实数m的取值范围.

查看试题解析
22. 在直角坐标系 $x O y$ 中，圆C的参数方程为 ${\begin{array}{l} x = - 6 + \cos t \\ y = - 1 + \sin t \end{array}$ （t为参数），在以坐标原点O为极点，x轴非负半轴为极轴建立的极坐标系中，直线l的极坐标方程为 $ρ \sin (θ - \frac{π}{4}) - \sqrt{2} = 0$ ．

(1)、求圆C的普通方程和直线l的直角坐标方程；

(2)、设点P是圆C上任一点，求点P到直线l距离的最小值．

查看试题解析
23. 已知函数 $f (x) = | 3 x - a | + a$ ， $a \in R$ ， $g (x) = | 3 x + 1 |$ .

(1)、当 $g (x) \geq 10$ 时，恒有 $f (x) \geq 9$ ，求a的最小值.

(2)、当 $x \in R$ 时，恒有 $f (x) + g (x) \geq 3$ ，求a的取值范围.

查看试题解析

临界值表
P（ $K^{2} \geq k_{0}$ ）	0.10	0.05	0.010	0.001
$k_{0}$	2.706	3.841	6.635	10.828