2020年浙江省中考数学分类汇编专题11 图形的相似
试卷更新日期：2020-07-06 类型：二轮复习
一、单选题
-
1. 如图，在Rt△ABC中，∠ACB=90°，以其三边为边向外作正方形，过点C作CR⊥FG于点R，再过点C作PQ⊥CR分别交边DE，BH于点P，Q。若QH=2PE，PQ=15，则CR的长为（ )
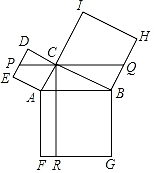A、14 B、15 C、8 D、62. 如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为2：5，且三角板的一边长为8cm，则投影三角板的对应边长为（ ）
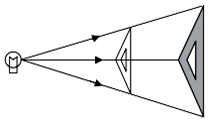A、20cm B、10cm C、8cm D、3.2cm3. 如图，在直角坐标系中，△OAB的顶点为O(0，0)，A(4，3)，B(3，0)。以点O为位似中心，在第三象限内作与△OAB的位似比为 的位似图形△OCD，则点C坐标为（ ）
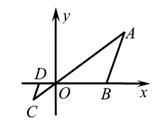A、(-1，-1). B、( ， -1) C、(-1， ) D、(-2，-1).4. 如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH . 连结EG，BD相交于点O，BD与HC相交于点P.若GO=GP，则 的值是（ ）
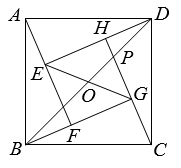A、 B、 C、 D、二、填空题
-
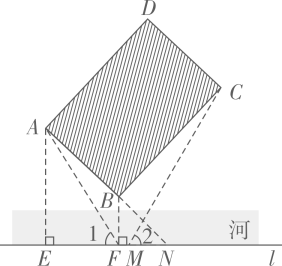
5. 如图，在河对岸有一矩形场地ABCD，为了估测场地大小，在笔直的河岸l上依次取点E，F，N，使AE⊥l，BF⊥l，点N，A，B在同一直线上。在F点观测A点后，沿FN方向走到M点.观测C点发现∠1=∠2。测得EF=15米，FM=2米，MN=8米，∠ANE=45°，则场地的边AB为米，BC为米。
6. 在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点，顶点都是格点的三角形称为格点三角形，如图，已知Rt△ABC是6×6网格图形中的格点三角形，则该图中所有与Rt△ABC相似的格点三角形中，面积最大的三角形的斜边长是.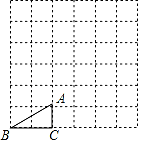
7. 如图是一张矩形纸片，点E在AB边上， 把△BCE沿直线CE对折， 使点B落在对角线AC上的点F处，连接DF。若点E，F，D在同一条直线上，AE=2，则DF= ， BE=。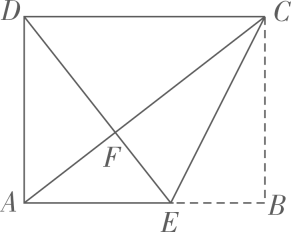
三、综合题
-
8. 已知在△ABC中，AC＝BC＝m，D是AB边上的一点，将∠B沿着过点D的直线折叠，使点B落在AC边的点P处（不与点A，C重合），折痕交BC边于点E.
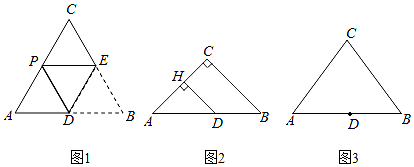(1)、特例感知：如图1，若∠C＝60°，D是AB的中点，求证：AP＝ AC；(2)、变式求异：如图2，若∠C＝90°，m＝ ，AD＝7，过点D作DH⊥AC于点H，求DH和AP的长；(3)、化归探究：如图3，若m＝10，AB＝12，且当AD＝a时，存在两次不同的折叠，使点B落在AC边上两个不同的位置，请直接写出a的取值范围.9. 如图，在正方形ABCD中，点E在BC边上， 连接AE、∠DAE的平分线AG与CD边交于点G，与BC的延长线交于点F，设 =λ(λ>0)。
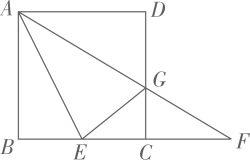(1)、若AB=2，λ=1，求线段CF的长。(2)、连接EG，若EG⊥AF，①求证：点G为CD的中点。
②求λ的值。
10. 如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，DE∥AC，EF∥AB。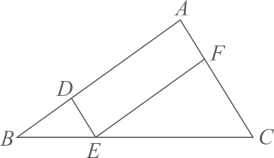
(1)、求证△BDE~△EFC。(2)、设①若BC=12，求线段BE的长。
②若△EFC的面积是20，求△ABC的面积。
11. 【性质探究】如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E。作DF⊥AE于点H，分别交AB，AC于点F，G。
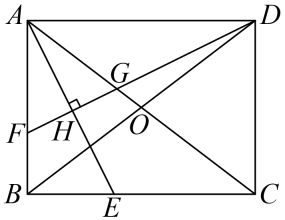(1)、判断△AFG的形状并说明理由。(2)、求证：BF=2OG。(3)、【迁移应用】记△DGO的面积为S1 ， △DBF的面积为S2 ， 当 时，求 的值。
(4)、【拓展延伸】若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF。当△BEF的面积为矩形ABCD面积的 时，请直接写出tan∠BAE的值。
12. 如图1，矩形DEFG中，DG=2，DE=3，Rt△ABC中，∠ACB=90°，CA=CB=2，FG，BC的延长线相交于点O，且FG⊥BC，OG=2，OC=4。将△ABC绕点O逆时针旋转α(0°≤α<180°)得到△A'B'C'。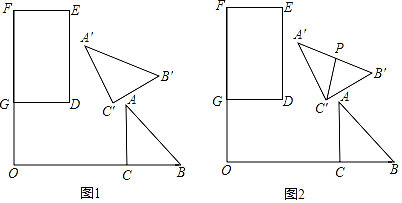
(1)、当α=30°时，求点C'到直线OF的距离。(2)、在图1中，取A'B'的中点P，连结C'P，如图2。①当C'P与矩形DEFG的一条边平行时，求点C'到直线DE的距离。
②当线段A'P与矩形DEFG的边有且只有一个交点时，求该交点到直线DG的距离的取值范围。
13. 如图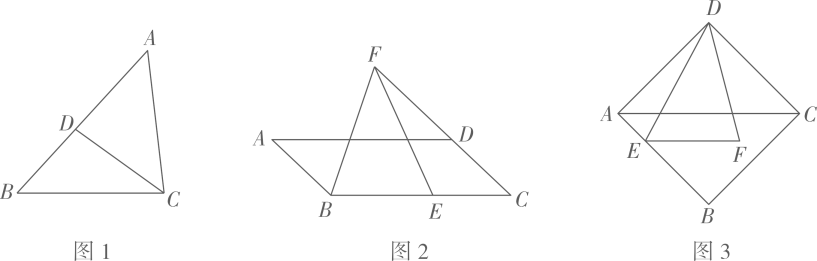
(1)、【基础巩固】如图1，在△ABC中，D为AB上一点，∠ACD=∠B.求证： .
(2)、【尝试应用】如图2，在 中，E为BC上一点，F为CD延长线上一点，∠BFE=∠A.若BF=4，BE=3，求AD的长.
(3)、【拓展提高】如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC=2EF， ，AE=2，DF=5，求菱形ABCD的边长.
14. 如图，在平面直角坐标系中，正方形ABOC的两直角边分别在坐标轴的正半轴上，分别过OB，OC的中点D，E作AE，AD的平行线，相交于点F， 已知OB=8.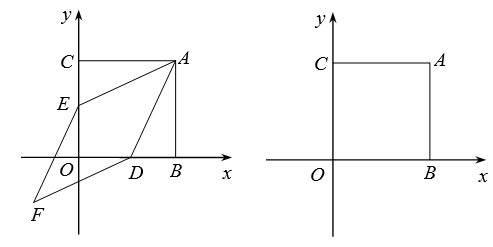
(1)、求证：四边形AEFD为菱形.(2)、求四边形AEFD的面积.(3)、若点P在x轴正半轴上(异于点D)，点Q在y轴上，平面内是否存在点G，使得以点A，P， Q，G为顶点的四边形与四边形AEFD相似？若存在，求点P的坐标；若不存在，试说明理由.