2020年浙江省中考数学分类汇编专题08 四边形
试卷更新日期:2020-07-06 类型:二轮复习
一、单选题
-
1. 下是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是( )A、由②推出③,由③推出① B、由①推出②,由②推出③ C、由③推出①,由①推出② D、由①推出③,由③推出②2. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
 A、 B、 C、 D、3. 把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )
A、 B、 C、 D、3. 把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )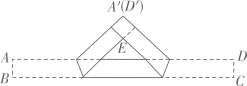 A、7+3 B、7+4 C、8+3 D、8+44. 如图,已知线段AB,分别以A,B为圆心,大于 AB同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是( )
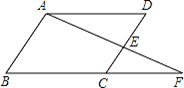
A、7+3 B、7+4 C、8+3 D、8+44. 如图,已知线段AB,分别以A,B为圆心,大于 AB同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是( )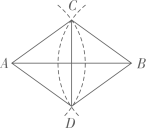 A、AB平分∠CAD B、CD平分∠ACB C、AB⊥CD D、AB=CD5. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作 BCDE,则∠E的度数为( )
A、AB平分∠CAD B、CD平分∠ACB C、AB⊥CD D、AB=CD5. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作 BCDE,则∠E的度数为( ) A、40° B、50° C、60° D、70°6. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变,如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′,若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )
A、40° B、50° C、60° D、70°6. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变,如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′,若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )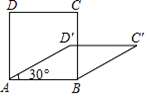 A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
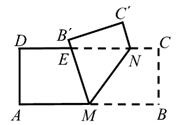
7. 如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N分别在边AB,CD上,CN=1cm。现将四边形BCNM沿MN折叠,使点B,C分别落在点B',C'上。当点B'恰好落在边CD上时,线段BM的长为cm;在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为cm。
 8. 如图, ABCD的对角线AC,BD相交于点O,请添加一个条件: , 使 ABCD是菱形。
8. 如图, ABCD的对角线AC,BD相交于点O,请添加一个条件: , 使 ABCD是菱形。 9. 图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E,OF⊥BD于点F,OE=OF=1cm,AC=BD=6cm, CE=DF, CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动.
9. 图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E,OF⊥BD于点F,OE=OF=1cm,AC=BD=6cm, CE=DF, CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动. (1)、当E,F两点的距离最大值时,以点A,B,C,D为顶点的四边形的周长是cm.(2)、当夹子的开口最大(点C与点D重合)时,A,B两点的距离为cm.10. 如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是°.
(1)、当E,F两点的距离最大值时,以点A,B,C,D为顶点的四边形的周长是cm.(2)、当夹子的开口最大(点C与点D重合)时,A,B两点的距离为cm.10. 如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是°.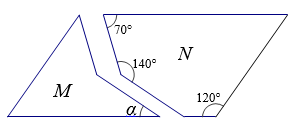 11. 图1是由七根连杆链接而成的机械装置,图2是其示意图.已知O,P两点固定,连杆PA=PC=140cm,AB=BC=CQ=QA=60cm,OQ=50cm,O,P两点间距与OQ长度相等。当OQ绕点O转动时,点A,B,C的位置随之改变,点B恰好在线段MN上来回运动。当点B运动至点M或N时,点A,C重合,点P,Q,A,B在同一直线上(如图3)。
11. 图1是由七根连杆链接而成的机械装置,图2是其示意图.已知O,P两点固定,连杆PA=PC=140cm,AB=BC=CQ=QA=60cm,OQ=50cm,O,P两点间距与OQ长度相等。当OQ绕点O转动时,点A,B,C的位置随之改变,点B恰好在线段MN上来回运动。当点B运动至点M或N时,点A,C重合,点P,Q,A,B在同一直线上(如图3)。 (1)、点P到MN的距离为cm。(2)、当点P,O,A在同一直线上时,点Q到MN的距离为cm。
(1)、点P到MN的距离为cm。(2)、当点P,O,A在同一直线上时,点Q到MN的距离为cm。三、综合题