2020年浙江省中考数学分类汇编专题03 方程与不等式
试卷更新日期:2020-07-06 类型:二轮复习
一、单选题
-
1. 用加减消元法解二元一次方程组: 时,下列方法中无法消元的是( )A、①×2-② B、②×(-3)-① C、①×(-2)+②. D、①-②×32. 若a>b,则( )A、a-1≥b B、b+1≥a C、a+1>b-1 D、a-1>b+13. 不等式3(1-x)>2-4x的解在数轴上表示正确的是( )A、
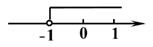 B、
B、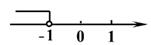 C、
C、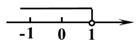 D、
D、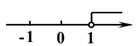 4. 不等式组 的解集在数轴上表示正确的是( )A、
4. 不等式组 的解集在数轴上表示正确的是( )A、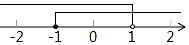 B、
B、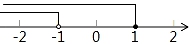 C、
C、 D、
D、 5. 已知关于x的一元二次方程 ,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关6. 某厂家2020年1~5月份的口罩产量统计如图所示。设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
5. 已知关于x的一元二次方程 ,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关6. 某厂家2020年1~5月份的口罩产量统计如图所示。设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( ) A、180(1-x)2=461 B、180(1+x)²=461 C、368(1-x)2=442 D、368(1+x)²=4427. 如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x,则列出方程正确的是( )
A、180(1-x)2=461 B、180(1+x)²=461 C、368(1-x)2=442 D、368(1+x)²=4427. 如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x,则列出方程正确的是( ) A、 B、 C、 D、8. 同型号的甲、乙两辆车加满气体燃料后均可行驶210km,它们各自单独行驶并返回的最远距离是105km,现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )A、120km B、140km C、160km D、180km9. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、
A、 B、 C、 D、8. 同型号的甲、乙两辆车加满气体燃料后均可行驶210km,它们各自单独行驶并返回的最远距离是105km,现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )A、120km B、140km C、160km D、180km9. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、二、填空题
-
10. 若分式 的值等于1,则x=。11. 一元一次方程2x+1=3的解是x=。12. 不等式组 的解为 。13. 若关于x,y的二元一次方程组 的解为 ,则多项式A可以是(写出一个即可)。14. 有两种消费券:A券,满60元减20元,B券,满90元减30元,即一次购物大于等于60元、90元,付款时分别减20元、30元.小敏有一张A券,小聪有一张B券,他们都购了一件标价相同的商品,各自付款,若能用券时用券,这样两人共付款150元,则所购商品的标价是元。15. 数学家斐波那契编写的《算经》中有如下问题:一组人平分10元钱,每人分得若干;若再加上6人,平分40元钱,则第二次每人所得与第一次相同,求第一次分钱的人数,设第一次分钱的人数为x人,则可列方程。
三、计算题
-
16. 计算(1)、计算: .(2)、解不等式: .17. 解方程组:18. 解不等式: .19. 解不等式组 .20. 以下是圆圆解方程 的解答过程。
解:去分母,得3(x+1)-2(x-3)=1。
去括号,得3x+1-2x+3=1。
移项,合并同类项,得x=-3。
圆圆的解答过程是否有错误?如果有错误,写出正确的解答过程。
21. 某经销商3月份用18000元购进一批T恤衫售完后,4月份用39000元购进一批相同的恤衫,数量是3月份的2倍,但每件进价涨了10元。(1)、4月份进了这批T恤衫多少件?(2)、4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元。甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同。①用含a的代数式表示b。
②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值。
22. 某企业承接了27000件产品的生产任务,计划安排甲、乙两个东间的共50名工人,合作生产20天完成.已知甲、乙两个车间利用现有设备,工人的工作效率为:甲车间每人每天生产25件,乙车间每人每天生产30件.(1)、求甲、乙两个车间各有多少名工人参与生产?(2)、为了提前完成生产任务,该企业设计了两种方案:方案一:甲车间租用先进生产设备,工人的工作效率可提高20%,乙车间维持不变;
方案二:乙车间再临时招聘若干名 工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
①求乙车间需临时招聘的工人数;
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.