四川省遂宁市蓬溪县2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-07-03 类型:期中考试
一、单选题
-
1. 下列有理式 中,分式有( )个A、1 B、2 C、3 D、42. 分式 中,最简分式有( )A、0个 B、1个 C、2个 D、3个3. 若把分式的x、y同时缩小12倍,则分式的值( )A、扩大12倍 B、缩小12倍 C、不变 D、缩小6倍4. 点(0,1)在( )A、x轴上 B、y轴上 C、第一象限 D、第三象限5. 函数y= 中,x的取值范围是( )A、x≠0 B、x>﹣2 C、x<﹣2 D、x≠﹣26. 一次函数 且y随x的增大而增大,则其图象可能是( )A、
 B、
B、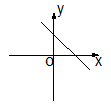 C、
C、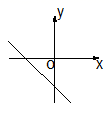 D、
D、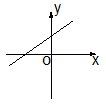 7. 如图,直线 经过点(2,0),则关于x的不等式 的解集是( )
7. 如图,直线 经过点(2,0),则关于x的不等式 的解集是( ) A、 B、 C、 D、8. 若关于x的分式方程 有增根,则m的值是( )A、m=-1 B、m=2 C、m=3 D、m=0或m=39. 关于 的方程: 的解是负数,则 的取值范围是A、 B、 且 C、 D、 且10. 已知反比例函数y= 的图上象有三个点(2,y1), (3, y2),(-1, y3),则y1、y2、y3的大小关系是( )A、y1>y2>y3 B、y2>y1>y3 C、y3>y1>y2 D、y3>y2>y111. 张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是
A、 B、 C、 D、8. 若关于x的分式方程 有增根,则m的值是( )A、m=-1 B、m=2 C、m=3 D、m=0或m=39. 关于 的方程: 的解是负数,则 的取值范围是A、 B、 且 C、 D、 且10. 已知反比例函数y= 的图上象有三个点(2,y1), (3, y2),(-1, y3),则y1、y2、y3的大小关系是( )A、y1>y2>y3 B、y2>y1>y3 C、y3>y1>y2 D、y3>y2>y111. 张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是 A、加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25 B、途中加油21升 C、汽车加油后还可行驶4小时 D、汽车到达乙地时油箱中还余油6升12. 如图,在平面直角坐标系中,点A是函数 在第一象限内图象上一动点,过点A分别作 轴于点 轴于点C, 分别交函数 的图象于点E、F,连接 .当点A的纵坐标逐渐增大时,四边形 的面积( )
A、加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25 B、途中加油21升 C、汽车加油后还可行驶4小时 D、汽车到达乙地时油箱中还余油6升12. 如图,在平面直角坐标系中,点A是函数 在第一象限内图象上一动点,过点A分别作 轴于点 轴于点C, 分别交函数 的图象于点E、F,连接 .当点A的纵坐标逐渐增大时,四边形 的面积( )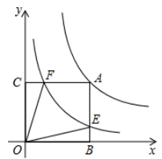 A、不变 B、逐渐变大 C、逐渐变小 D、先变大后变小
A、不变 B、逐渐变大 C、逐渐变小 D、先变大后变小二、填空题
-
13. 当x=时,分式 的值为0.14. 在现代科学技术中,纳米是一种长度单位,1纳米等于十亿分之一米(即1纳米= 米),经科学检测,新冠病毒的直径约为100纳米,用科学记数法表示:100纳米=米。15. 点A(-3,2)关于y轴对称的点的坐标为 .16. 将直线 y=-x-3向上平移5个单位,得到直线17. 若函数y=kx+b的图象平行于直线y=2x,且过点(2,﹣4),则该函数的表达式是 .18. 直线 与两坐标轴围成的三角形的面积为4,则b的值为.19. 如图,在反比例函数 的图象上,有点 , , , ,它们的横坐标依次为1,2,3,4,分别过这些点作 轴与 轴的垂线,图中所构成的阴影部分的面积从左到右依次为 , , ,则 + + =
 20. 将x= 代入反比例函数y=- 中,所得的函数值记为y1 , 又将x= y1+1代入反比例函数y=- 中,所得的函数值记为y2 , 又将x= y2+1代入反比例函数y=- 中,所得的函数值记为y3 , …,如此继续下去,则y2020=
20. 将x= 代入反比例函数y=- 中,所得的函数值记为y1 , 又将x= y1+1代入反比例函数y=- 中,所得的函数值记为y2 , 又将x= y2+1代入反比例函数y=- 中,所得的函数值记为y3 , …,如此继续下去,则y2020=三、解答题
-
21. 计算:(1)、(2)、22. 解方程: .23. 先化简: ,若﹣2≤x≤2,请你选择一个恰当的x值(x是整数)代入求值.24. 某市在旧城改造过程中,需要整修一段全长2400米的道路,为了尽量减少施工对城市交通所造成的影响,实际工作效率比原计划提高了20%,结果提前8小时完成任务,求原计划每小时修路的长度。25. 甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.
 (1)、求甲车从A地到达B地的行驶时间;(2)、求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(1)、求甲车从A地到达B地的行驶时间;(2)、求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)、求乙车到达A地时甲车距A地的路程.26. 抗击“新冠疫情”期间,某种消毒液A市需要6吨,B市需要8吨,正好M市储备有10吨,N市储备有4吨,预防“新冠疫情”领导小组决定将这14吨消毒液调往A市和B市,消毒液每吨的运费价格如下表。设从M市调运x吨到A市.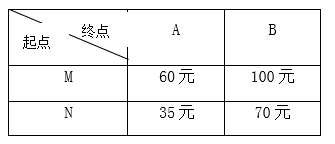 (1)、求调运14吨消毒液的总运费y关于x的函数关系式;(2)、求出总运费最低的调运方案,最低运费的多少?27. 如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线 在第一象限内交于点C(1,m),直线CQ的解析式为:y=kx+b(k≠0)
(1)、求调运14吨消毒液的总运费y关于x的函数关系式;(2)、求出总运费最低的调运方案,最低运费的多少?27. 如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线 在第一象限内交于点C(1,m),直线CQ的解析式为:y=kx+b(k≠0)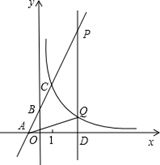 (1)、求m和n的值;(2)、过x轴上的点D(3,0)作平行于y轴的直线l,分别与直线AB和双曲线 交于点P、Q,求△APQ的面积.(3)、直接写出 的解集(4)、直接写出直方程 的解。
(1)、求m和n的值;(2)、过x轴上的点D(3,0)作平行于y轴的直线l,分别与直线AB和双曲线 交于点P、Q,求△APQ的面积.(3)、直接写出 的解集(4)、直接写出直方程 的解。