四川省绵阳市三台县2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-07-03 类型：期中考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{a - 1}$ 在实数范围内有意义，则a的取值范围是（　　）

A、a＞1 B、a≥1 C、a＝1 D、a≤1

查看试题解析
2. 下列各式中，最简二次根式是（）

A、 $\sqrt{x^{2} + y^{2}}$ B、 $\sqrt{7 a b^{3}}$ C、 $\sqrt{8}$ D、 $\sqrt{0.2}$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{3} = \sqrt{6}$ B、 $\sqrt{3} \times \sqrt{3} =2 \sqrt{3}$ C、 $\sqrt{3} + \sqrt{3} =2 \sqrt{3}$ D、 $2+ \sqrt{3} =2 \sqrt{3}$

查看试题解析
4. 若 $\sqrt{12 n}$ 是整数，则正整数n的最小值是（）

A、2 B、3 C、4 D、6

查看试题解析
5. 有一个直角三角形的两边长分别为5和12，则第三边长为（）

A、13 B、 $\sqrt{119}$ C、13或 $\sqrt{119}$ D、无法确定

查看试题解析
6. 不能判定四边形ABCD为平行四边形的题设是（）

A、AB＝CD，AB∥CD B、∠A＝∠C，∠B＝∠D C、AB＝AD，BC＝CD D、AB＝CD，AD＝BC

查看试题解析
7. 如图，25和169分别是两个正方形的面积，字母B所代表的正方形的面积是（）

A、12 B、13 C、144 D、194

查看试题解析
8. 如图，在四边形ABCD中，∠DAB=90°，∠DCB=90°，E、F分别是BD、AC的中点，AC=6，BD=10，则EF的长为（）

A、3 B、4 C、5 D、 $\sqrt{7}$

查看试题解析
9. 如图，顺次连接四边形ABCD各边中点，得到四边形EFGH，下列条件中，可使四边形EFGH是矩形的是（）

A、AB=CD B、AC⊥BD C、AC=BD D、AD∥BC

查看试题解析
10. 如图，△ABC中，AB=8，AC=6，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F ，交AB于G ，连接EF ，则线段EF的长是（）

A、3 B、4 C、1 D、0.5

查看试题解析
11. 已知 $a - \frac{1}{a} = \sqrt{6}$ ，则 $a + \frac{1}{a} =$ （）

A、 $\sqrt{10}$ B、 $\pm \sqrt{10}$ C、 $\pm 2$ D、 $2 \sqrt{2}$

查看试题解析
12. 如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S_△AOE：S_△BCM=2：3．其中正确结论的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

13. 计算：( $- \sqrt{5}$ )²=。

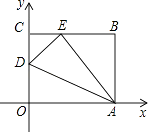
查看试题解析
14. 若最简二次根式 $\sqrt{1 + a}$ 与 $\sqrt{4 - 2 a}$ 的被开方数相同，则a的值为.

查看试题解析
15. 在平行四边形ABCD中，对角线AC和BD相交于点O，AB=6cm ， AC+BD=14cm ，则△AOB的周长为．

查看试题解析
16. 如图，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，则D点的坐标是．

查看试题解析
17. 如图所示的圆柱体中底面圆的半径是 $\frac{2}{π}$ ，高为2，若一只小虫从A点出发沿着圆柱体的侧面爬行到C点，则小虫爬行的最短路程是．（结果保留根号）．

查看试题解析
18. 如图，将n个边长都为1cm的正方形按如图所示摆放，点A1， A2，…，An分别是正方形的中心，则n个正方形重叠形成的重叠部分的面积和为

查看试题解析

三、解答题

19. 计算：

(1)、 $4 \sqrt{5} + \sqrt{45} - \sqrt{20}$

(2)、 ${(\sqrt{3} - 2)}^{2019} {(\sqrt{3} + 2)}^{2020} - 2 | \frac{\sqrt{3}}{2} - 1 | - {(\sqrt{2})}^{0}$

查看试题解析
20. 实数a ， b在数轴上对应点A ， B的位置如图，化简 $| a + b | - \sqrt{b^{2}} - \sqrt{{(a - b)}^{2}}$ .

查看试题解析
21. 如图，在△ABC中，∠C=90°，∠A=30°，BD是∠ABC的平分线，CD=5cm，求AB的长．

查看试题解析
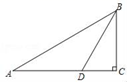22. 如图，E、F是平行四边形ABCD的对角线AC上的两点，AE＝CF ．求证：四边形DEBF是平行四边形．

查看试题解析
23. 如图所示，在四边形ABCD中，AD∥BC，AD=24cm ， BC=30cm ，点P从A向点D以1cm/s的速度运动，到点D即停止．点Q从点C向点B以2cm/s的速度运动，到点B即停止．直线PQ将四边形ABCD截得两个四边形，分别为四边形ABQP和四边形PQCD，则当P，Q两点同时出发，几秒后所截得两个四边形中，其中一个四边形为平行四边形？

查看试题解析
24. 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE//AC，且DE：AC=1：2，连接CE、OE，连接AE交OD于点F．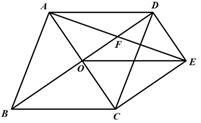

(1)、求证：OE=CD；

(2)、若菱形ABCD的边长为2，∠ABC=60°，求AE的长．

查看试题解析
25. 如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．

(1)、探究：线段OE与OF的数量关系并加以证明；

(2)、当点O在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明；若不是，则说明理由；

(3)、当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？

查看试题解析