四川省简城学区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-07-03 类型:期中考试
一、单选题
-
1. 下列图形既是轴对称图形又是中心对称图形的是( )A、平行四边形 B、等边三角形 C、等腰梯形 D、圆2. 等腰三角形一个角是50°,则它的底角的度数为( )A、50° B、50°或 80° C、50°或 65° D、65°3. 若a<b , 则下列不等式不一定成立的是()A、a+2<b+2 B、2a<2b C、 D、a2<b24. △ABC中,∠B=50°,∠A=80°,若AB=6,则AC=( )A、6 B、8 C、5 D、135. 下列命题,假命题是( )A、有一个内角等于60°的等腰三角形是等边三角形 B、有一个角是40°,腰相等的两个等腰三角形全等 C、在直角三角形中,最大边的平方等于其他两边的平方和 D、三角形两个内角平分线的交点到三边的距离相等6. 如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是( )
 A、2
A、2 B、2
C、4
B、2
C、4  D、4
7. 某市出租车的收费标准是:起步价为8元(即行驶距离不超过3km , 都需付8元车费),超过3km后,每增加1km , 加收1.5元(不足1km按1km计算).某人从甲地到乙地经过的路程是xkm , 出租车费为15.5元,那么x的最大值是( )A、11 B、8 C、7 D、58. 关于x的一元一次不等式
D、4
7. 某市出租车的收费标准是:起步价为8元(即行驶距离不超过3km , 都需付8元车费),超过3km后,每增加1km , 加收1.5元(不足1km按1km计算).某人从甲地到乙地经过的路程是xkm , 出租车费为15.5元,那么x的最大值是( )A、11 B、8 C、7 D、58. 关于x的一元一次不等式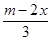 ≤﹣2的解集为x≥4,则m的值为( ) A、14 B、7 C、﹣2 D、29. 如图,已知函数y1=3x+b和y2=ax﹣3的图象交于点P(﹣2,﹣5),则不等式3x+b>ax﹣3的解集为( )
≤﹣2的解集为x≥4,则m的值为( ) A、14 B、7 C、﹣2 D、29. 如图,已知函数y1=3x+b和y2=ax﹣3的图象交于点P(﹣2,﹣5),则不等式3x+b>ax﹣3的解集为( )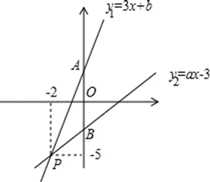 A、x>﹣2 B、x<﹣2 C、x>﹣5 D、x<﹣510. 中, ,将 绕点A逆时针旋转后,能与 重合,如果 ,那么 的长等于A、3 B、 C、 D、不能确定
A、x>﹣2 B、x<﹣2 C、x>﹣5 D、x<﹣510. 中, ,将 绕点A逆时针旋转后,能与 重合,如果 ,那么 的长等于A、3 B、 C、 D、不能确定二、填空题
-
11. 如图,△ABC与△BDE都是等腰直角三角形,若△ABC经旋转后能与△BDE重合,则旋转中心是 , 旋转了°.
 12. 已知点P(m﹣2,2m﹣1)在第二象限,则实数m的取值范围是 .13. 如图,在△ABC中,AB=a,AC=b,BC边上的垂直平分线DE交BC、AB分别于点D、E, 则△AEC的周长等于 。
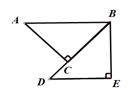
12. 已知点P(m﹣2,2m﹣1)在第二象限,则实数m的取值范围是 .13. 如图,在△ABC中,AB=a,AC=b,BC边上的垂直平分线DE交BC、AB分别于点D、E, 则△AEC的周长等于 。 14. 如图,在△ABC中∠ACB=90°,AC=BC , AE是BC边上的中线CF⊥AE , 垂足为F , BD⊥BC交CF的延长线于D . 若AC=12cm , 则BD= .
14. 如图,在△ABC中∠ACB=90°,AC=BC , AE是BC边上的中线CF⊥AE , 垂足为F , BD⊥BC交CF的延长线于D . 若AC=12cm , 则BD= . 15. 不等式组 的解集是 ,则a的取值范围是 .16. 一个面积为 的等腰三角形,它的一个内角是30°,则以它的腰长为边长的正方形面积为 .17. 如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形三边距离之和PD+PE+PF的值是 .
15. 不等式组 的解集是 ,则a的取值范围是 .16. 一个面积为 的等腰三角形,它的一个内角是30°,则以它的腰长为边长的正方形面积为 .17. 如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形三边距离之和PD+PE+PF的值是 .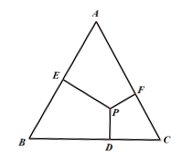 18. 如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,……Bn-1Bn是△ABn-2Bn-1的高,则B4B5的长是 , 猜想Bn-1Bn的长是 .
18. 如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,……Bn-1Bn是△ABn-2Bn-1的高,则B4B5的长是 , 猜想Bn-1Bn的长是 . 19. 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是.
19. 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是.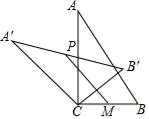
三、解答题
-
20.(1)、解不等式: ,并把它的解集表示在数轴上;(2)、解不等式组 ,并写出它的所有非负整数解.21. 如图,在建立平面直角坐标系的网格纸中,每个小方格都是边长为1个单位长度的小正方形,△ABC的顶点均在格点上,点P的坐标为(-1,0).
 (1)、把△ABC绕点P旋转180°得到△A’B’C’ , 作出△A’B’C’;(2)、把△ABC向右平移7个单位长度得到△A″B″C″,作出△A″B″C″;(3)、△A’B’C’与△A″B″C″是否成中心对称?若是,则找出对称中心P’ , 并写出其坐标;若不是,请说明理由.22. 已知关于x , y的方程组 的解,x , y均为负数.(1)、求m的取值范围;(2)、化简:|m-5|+|m+1|23. 如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.
(1)、把△ABC绕点P旋转180°得到△A’B’C’ , 作出△A’B’C’;(2)、把△ABC向右平移7个单位长度得到△A″B″C″,作出△A″B″C″;(3)、△A’B’C’与△A″B″C″是否成中心对称?若是,则找出对称中心P’ , 并写出其坐标;若不是,请说明理由.22. 已知关于x , y的方程组 的解,x , y均为负数.(1)、求m的取值范围;(2)、化简:|m-5|+|m+1|23. 如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.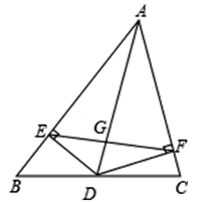 (1)、求证:AD垂直平分EF;(2)、若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.24. 在今年年初,新型冠状病毒在武汉等地区肆虐,为了缓解湖北地区的疫情,全国各地的医疗队员都纷纷报名支援湖北,某方舱医院需要8组医护人员支援,要求每组分配的人数相同,若按每组人数比预定人数多分配1人,则总数会超过100人,若每组人数比预定人数少分配一人,则总数不够90人,那么预定每组分配的人数是多少人?25. 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)、求证:AD垂直平分EF;(2)、若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.24. 在今年年初,新型冠状病毒在武汉等地区肆虐,为了缓解湖北地区的疫情,全国各地的医疗队员都纷纷报名支援湖北,某方舱医院需要8组医护人员支援,要求每组分配的人数相同,若按每组人数比预定人数多分配1人,则总数会超过100人,若每组人数比预定人数少分配一人,则总数不够90人,那么预定每组分配的人数是多少人?25. 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.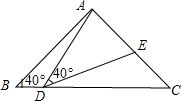 (1)、当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)、当DC等于多少时,△ABD≌△DCE,请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.26. 2020年年初,在我国湖北等地区爆发了新型冠状病毒引发的肺炎疫情,对此湖北武汉率先采取了“封城”的措施,为了解决武汉市民的生活物资紧缺问题,某省给武汉捐献一批水果和蔬菜共435吨,其中蔬菜比水果多97吨.(1)、求蔬菜和水果各有多少吨?(2)、某慈善组织租用甲、乙两种货车共16辆,已知一辆甲车同时可装蔬菜18吨,水果10吨;一辆乙车同时可装蔬菜16吨,水果11吨;若将这批货物一次性运到武汉,有哪几种租车方案?请你帮忙设计出来.(3)、若甲种货车每辆需付燃油费1600元,乙种货车每辆需付燃油费1200元,应选(2)中的那种方案,才能使所付的燃油费最少?最少的燃油费是多少元?27. 如图,在平面直角坐标系中,点A、B的坐标分别是(0,8),(6,0),连接AB , 将△AOB沿过点B的直线折叠,使点A落在x轴上的点A'处,折痕所在直线交y轴正半轴于点C .
(1)、当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)、当DC等于多少时,△ABD≌△DCE,请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.26. 2020年年初,在我国湖北等地区爆发了新型冠状病毒引发的肺炎疫情,对此湖北武汉率先采取了“封城”的措施,为了解决武汉市民的生活物资紧缺问题,某省给武汉捐献一批水果和蔬菜共435吨,其中蔬菜比水果多97吨.(1)、求蔬菜和水果各有多少吨?(2)、某慈善组织租用甲、乙两种货车共16辆,已知一辆甲车同时可装蔬菜18吨,水果10吨;一辆乙车同时可装蔬菜16吨,水果11吨;若将这批货物一次性运到武汉,有哪几种租车方案?请你帮忙设计出来.(3)、若甲种货车每辆需付燃油费1600元,乙种货车每辆需付燃油费1200元,应选(2)中的那种方案,才能使所付的燃油费最少?最少的燃油费是多少元?27. 如图,在平面直角坐标系中,点A、B的坐标分别是(0,8),(6,0),连接AB , 将△AOB沿过点B的直线折叠,使点A落在x轴上的点A'处,折痕所在直线交y轴正半轴于点C .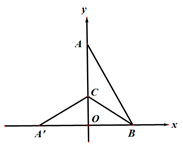 (1)、求直线BC的函数表达式;(2)、把直线BC向左平移,使之经过点A' , 求平移后直线的函数表达式.28. 已知Rt△ABC中,∠BAC=90°,AB=AC , 点E为△ABC内一点,连接AE , CE , CE⊥AE , 过点B作BD⊥AE , 交AE的延长线于D .
(1)、求直线BC的函数表达式;(2)、把直线BC向左平移,使之经过点A' , 求平移后直线的函数表达式.28. 已知Rt△ABC中,∠BAC=90°,AB=AC , 点E为△ABC内一点,连接AE , CE , CE⊥AE , 过点B作BD⊥AE , 交AE的延长线于D . (1)、如图1,求证BD=AE;(2)、如图2,点H为BC中点,分别连接EH , DH , 求∠EDH的度数;(3)、如图3,在(2)的条件下,点M为CH上的一点,连接EM , 点F为EM的中点,连接FH , 过点D作DG⊥FH , 交FH的延长线于点G , 若GH:FH=6:5,△FHM的面积为30,∠EHB=∠BHG , 求线段EH的长.
(1)、如图1,求证BD=AE;(2)、如图2,点H为BC中点,分别连接EH , DH , 求∠EDH的度数;(3)、如图3,在(2)的条件下,点M为CH上的一点,连接EM , 点F为EM的中点,连接FH , 过点D作DG⊥FH , 交FH的延长线于点G , 若GH:FH=6:5,△FHM的面积为30,∠EHB=∠BHG , 求线段EH的长.