天津市和平区2019-2020学年七年级下学期线上数学期中考试试卷

试卷更新日期：2020-07-03 类型：期中考试

进入出卷网下载

一、单选题

1. 64的立方根是（）

A、4 B、8 C、±8 D、2

查看试题解析
2. 估计 $\sqrt{7}$ 的值在（）

A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间

查看试题解析
3. 下面四个点位于第四象限的是（）

A、 $(- 1, 2)$ B、 $(- 2, - 2)$ C、 $(2, 5)$ D、 $(6, - 2)$

查看试题解析
4. 点A为直线a外一点，点B是直线 a上一点，点 A到直线a的距离为5cm，则AB的长度可能为（）

A、2cm B、3cm C、4cm D、18cm

查看试题解析
5. 将点 $P (1, - 5)$ 向左平移 $3$ 个单位，再向上平移6个单位，得到点Q，点Q的坐标为（）

A、 $(- 2, 1)$ B、 $(4, 1)$ C、 $(4, - 11)$ D、 $(- 2, - 11)$

查看试题解析
6. 已知小明从点O出发，先向西走10米，再向南走20米，到达点M，如果点M的位置用 $(- 10 ， - 20)$ 表示，那么 $(10 ， - 10)$ 表示的位置是（）

A、A B、B C、C D、D

查看试题解析
7. 已知点A在第二象限，到 x轴的距离是5，到y轴的距离是6，点A的坐标为（）

A、 $(- 5 ， 6)$ B、 $(- 6 ， 5)$ C、 $(5 ， - 6)$ D、 $(6 ， - 5)$

查看试题解析
8. 下列各组数中，是方程组 ${\begin{array}{l} x + y = 8 \\ x - y = 4 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 6 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 5 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 7 \\ y = - 1 \end{array}$

查看试题解析
9. 小亮的妈妈用28元钱买了甲乙两种水果，甲种水果每千克4元，乙种水果每千克6元，且乙种水果比甲种水果多买了2千克，求小亮妈妈两种水果各买了多少千克？设小亮妈妈买了甲种水果x千克，乙种水果y千克，则可列方程组为（）

A、 ${\begin{array}{l} 4 x + 6 y = 28 \\ x = y + 2 \end{array}$ B、 ${\begin{array}{l} 6 x + 4 y = 28 \\ x = y + 2 \end{array}$ C、 ${\begin{array}{l} 4 x + 6 y = 28 \\ x = y - 2 \end{array}$ D、 ${\begin{array}{l} 6 x + 4 y = 28 \\ x = y - 2 \end{array}$

查看试题解析
10. 在以下说法中：①实数分为正有理数、0、负有理数．②实数和数轴上的点一一对应． ③过直线外一点有且只有一条直线和已知直线垂直．④过一点有且只有一条直线和已知直线平行．⑤假命题不是命题．⑥如果两条直线都和第三条直线平行，那么这两条直线也互相平行．⑦若一个数的立方根和平方根相同，那么这个数只能是0．其中说法正确的个数是（）

A、3 B、4 C、5 D、6

查看试题解析
11. 已知， $E F / / A B ， C D ⊥ D F$ ，判断 $∠ 1 ， ∠ 2 ， ∠ 3$ 之间的关系满足（）

A、 $∠ 1 + ∠ 2 + ∠ 3 = 180^{°}$ B、 $∠ 2 = ∠ 3 + ∠ 1$ C、 $∠ 1 + ∠ 2 - ∠ 3 = 90^{°}$ D、 $∠ 2 + ∠ 3 - ∠ 1 = 90^{°}$

查看试题解析
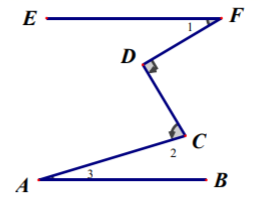12. 已知关于x,y的方程组 ${\begin{array}{l} 4 x - y = - 5 \\ a x + b y = - 1 \end{array}$ 和 ${\begin{array}{l} 3 x + y = - 9 \\ 3 a x + 4 b y = 18 \end{array}$ 有相同的解，那么 $\sqrt{a + b}$ 的平方根是（）

A、0 B、±1 C、 $\pm \sqrt{2}$ D、±2

查看试题解析

二、填空题

13. 已知如图，若满足，则可以判定 $A B / / C D$ ．（仅可添加一个条件）

查看试题解析
14. 如图，同旁内角有对．

查看试题解析
15. 某楼梯的截面如图，其中 $E R = 5 ， R Q = 10$ ，若在楼梯上铺设地毯，至少需要米．

查看试题解析
16. 比较下列各数的大小关系：
① 2 $\sqrt{2} + 1$ ，② $\frac{\sqrt{5} + 1}{2}$ 2，③ $\sqrt{2}$ $\sqrt[3]{3}$

查看试题解析
17. 已知 $Δ A B C$ 的面积为16，其中两个顶点的坐标分别是 $A (- 7, 0), B (1, 0)$ ，顶点C在y轴上，那么点C的坐标为

查看试题解析

三、解答题

18. 阅读材料后完成．
有这样一个游戏，游戏规则如下所述：如图①—图④，都是边长为1的 $5 \times 5$ 网格图，其中每条实线称为格线，格线与格线的交点称为格点．在图①和图②中，可知 $E F ⊥ E H ， L M ⊥ A B$ ．在图③ 和图④中，可知 $C D / / A B$ ．根据上面的游戏规则，同学们开始闯关吧！第一关：在图⑤的 $6 \times 6$ 网格图中，所给各点均为格点，经过给定的一点（不包括边框上的点），在图中画出一条与线段AB垂直的线段（或者直线）BC，再画出与线段AB平行的一条线段（或者直线）EF．第二关：在图⑥的 $6 \times 6$ 网格图中，所给各点均为格点，经过两对给定的点，构造两条互相垂直的直线．（在图中直接画出）

查看试题解析
19. 计算：

(1)、 $\sqrt[3]{- 27} - \sqrt{{(- π)}^{2}} - | π - 3 |$

(2)、 $3 - \sqrt{3} (\sqrt{3} - 1) - \sqrt{3}$

查看试题解析
20. 解下列二元一次方程组

(1)、 ${\begin{array}{l} 2 x + 5 = - 14 \\ 2 x - y = - 2 \end{array}$

(2)、 ${\begin{array}{l} 3 (x + 1) = 2 y - 7 \\ \frac{2 x + 1}{3} = - \frac{1}{2} y \end{array}$

查看试题解析
21. 已知如图，在 $Δ A B C$ 中，三个顶点的坐标分别为 $A (2 ， 3) ， B (5 ， - 1) ， C (1 ， 1)$ ，将 $Δ A B C$ 沿 x轴负方向平移4个单位长度，再沿y轴负方向平移2个单位长度，得到 $Δ D E F$ ，其中点A的对应点为点D，点B的对应点为点E，点C的对应点为点F

(1)、直接写出平移后的 $Δ D E F$ 的顶点坐标：
DEF

(2)、在坐标系中画出平移后的 $Δ D E F .$

(3)、求出 $Δ D E F$ 的面积．

查看试题解析
22. 已知如图， $Δ A B C$ 过点 A做 $∠ D A E = ∠ B A C ，$ 且 $A D / / B C ， ∠ 1 = ∠ 2$

(1)、求证 $A B / / D E .$

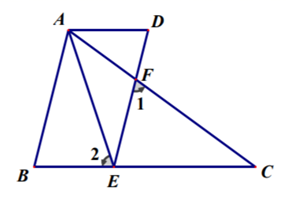(2)、若已知AE平分 $∠ B A C ， ∠ C = 35^{°}$ ，求 $∠ B A D$ 的度数

查看试题解析
23. 现有36卷相同的布料做工作服，每卷布料可制作成上衣25件，或者制作成裤子40件，一件上衣和两件裤子组成一套，问，用多少卷布料制作上衣，多少卷布料制作裤子可以使上衣和裤子正好配套？

查看试题解析
24. 已知， $Δ A B C$ ，点E是直线AC上一个动点（不与A，C重合），点F是BC边上一个定点，过点E作 $D E / / B C$ ，交直线AB于点D，连接BE，过点F作 $F G / / B E$ ，交直线AC于点G．

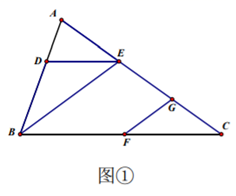(1)、如图①，当点E在线段AC上时，求证： $∠ D E B = ∠ G F C$ ．

(2)、在（1）的条件下，判断 $∠ D E C 、 ∠ E G F 、 ∠ B F G$ 这三个角的度数和是否为一个定值？如果是，求出这个值，如果不是，说明理由．

(3)、如图②，当点E在线段 AC的延长线上时，（2）中的结论是否仍然成立？如果不成立，请直接写出 $∠ D E C 、 ∠ E G F 、 ∠ B F G$ 之间的关系．

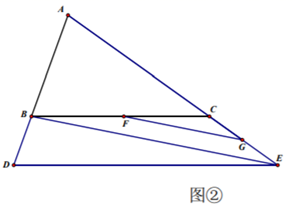(4)、当点E在线段CA的延长线上时，（2）中的结论是否仍然成立？如果不成立，请直接写出 $∠ D E C 、 ∠ E G F 、 ∠ B F G$ 之间的关系．

查看试题解析
25. 如图，在长方形 $O A B C$ 中，O为平面直角坐标系的原点，点A的坐标为 $(a ， 0)$ ，点C的坐标为 $(0 ， b)$ 且a，b满足 $\sqrt{a - 8} + | b - 12 | = 0$ ，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着 $O - A - B - C - O$ 的线路移动．

(1)、求点B的坐标为；当点P移动5秒时，点P的坐标为

(2)、在移动过程中，当点P移动11秒时，求 $Δ O P B$ 的面积．

(3)、在 $(2)$ 的条件下，坐标轴上是否存在点Q，使 $Δ O P Q$ 的面积与 $Δ O P B$ 的面积相等，若存在，求点Q的坐标；若不存在，说明理由．

查看试题解析