四川省成都市天府新区六校2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-07-03 类型:期中考试
一、单选题
-
1. 如果一个角是50°,那么它的余角的度数是( )A、40° B、50° C、100° D、130°2. 小明上网查得H7N9禽流感病毒的直径大约是0.00000008米,用科学记数法表示为( )A、 B、 C、 D、3. 下列长度的3条线段,能首尾依次相接组成三角形的是( ).A、1,3,5 B、3,4,6 C、5,6,11 D、8,5,24. 下列运算正确的是( )A、 B、 C、 D、5. 下列乘法中,不能运用平方差公式进行运算的是( ).A、 B、 C、 D、6. 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的根据是( ).
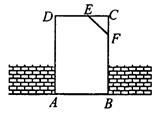 A、三角形的稳定性 B、长方形的对称性 C、长方形的四个角都是直角 D、两点之间线段最短7. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )
A、三角形的稳定性 B、长方形的对称性 C、长方形的四个角都是直角 D、两点之间线段最短7. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )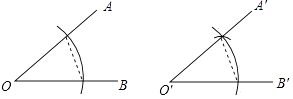 A、SAS B、ASA C、AAS D、SSS8. 某星期天小李步行取图书馆看书,途中遇到一个红灯,停下来耽误了几分钟,为了赶时间,他以更快速度步行到图书馆,下面几幅图是步行路程s(米)与行进时间t(分)的关系的示意图,你认为正确的是( )A、
A、SAS B、ASA C、AAS D、SSS8. 某星期天小李步行取图书馆看书,途中遇到一个红灯,停下来耽误了几分钟,为了赶时间,他以更快速度步行到图书馆,下面几幅图是步行路程s(米)与行进时间t(分)的关系的示意图,你认为正确的是( )A、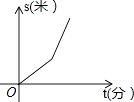 B、
B、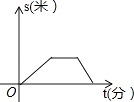 C、
C、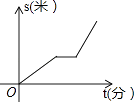 D、
D、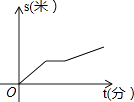 9. 下列说法中正确的个数有( ).
9. 下列说法中正确的个数有( ).⑴在同一平面内,不相交的两条直线必平行
⑵同旁内角互补
⑶相等的角是对顶角
⑷从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
⑸经过直线外一点,有且只有一条直线与已知直线平行
A、1个 B、3个 C、4个 D、5个10. 如图,△ABC中, ,延长BC到D,∠ABC与∠ACD的平分线相交于点A1 , 与 的平分线相交于点A2 , 依此类推, 与 的平分线相交于点An , 则 的度数为( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为;12. 若 , ,则 .13. 如图,将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2=°.
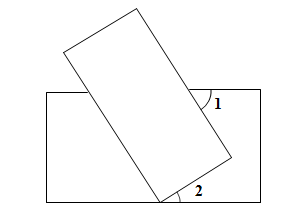 14. 若 是一个完全平方式,则m的值是 .15. 已知a-b=4,则 的值为 .16. 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠CFC′=150°,则∠AED′= .
14. 若 是一个完全平方式,则m的值是 .15. 已知a-b=4,则 的值为 .16. 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠CFC′=150°,则∠AED′= . 17. 已知代数式 可以利用完全平方公式变形为 ,进而可知 的最小值是4.依此方法,代数式 的最小值是 .18. 在△ABC中,∠ABC=45 ,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,下列结论:
17. 已知代数式 可以利用完全平方公式变形为 ,进而可知 的最小值是4.依此方法,代数式 的最小值是 .18. 在△ABC中,∠ABC=45 ,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,下列结论:①∠FCD=45
②AE=EC
③S△ABF:S△AFC=AD:FD
④若BF=2EC,则△FDC周长等于AB的长.
正确结论的序号是 .
 19. 有一系列等式:
19. 有一系列等式:1×2×3×4+1=52=(12+3×1+1)2 ,
2×3×4×5+1=112=(22+3×2+1)2 ,
3×4×5×6+1=192=(32+3×3+1)2 ,
4×5×6×7+1=292=(42+3×4+1)2 ,
……
⑴根据你的观察,归纳发现规律,写出9×10×11×12+1的结果是 ;
⑵式子(n-1) n (n+1) (n+2)+1= .
三、解答题
-
20. 计算(1)、(2)、21. 先化简,再求值:[(2x+y)2﹣y(y+4x)﹣8xy]÷(﹣2x).其中x=2,y=﹣1.22. 阅读下列推理过程,在括号中填写理由.
已知:如图,点D、E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2( ▲ )
∵AC∥DE(已知)
∴∠1=∠3( ▲ )
故∠2=∠3( ▲ )
∵DF∥AE(已知)
∴∠2=∠5,( ▲ )
∠3=∠4( ▲ )
∴∠4=∠5( ▲ )
∴DF平分∠BDE( ▲ )
 23. 如图,在Rt△ABE中,∠AEB=90°,C为AE延长线上的一点,D为AB边上的一点,DC交BE于F,若∠ADC=80°,∠B=30°,求∠C的度数.
23. 如图,在Rt△ABE中,∠AEB=90°,C为AE延长线上的一点,D为AB边上的一点,DC交BE于F,若∠ADC=80°,∠B=30°,求∠C的度数. 24. 如图所示,小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况.
24. 如图所示,小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况. (1)、图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?(2)、他到达离家最远的地方是什么时间?离家多远?(3)、10时到12时他行驶了多少千米?(4)、他可能在哪段时间内休息,并吃午餐?(5)、他由离家最远的地方返回时的平均速度是多少?25. 以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.
(1)、图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?(2)、他到达离家最远的地方是什么时间?离家多远?(3)、10时到12时他行驶了多少千米?(4)、他可能在哪段时间内休息,并吃午餐?(5)、他由离家最远的地方返回时的平均速度是多少?25. 以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.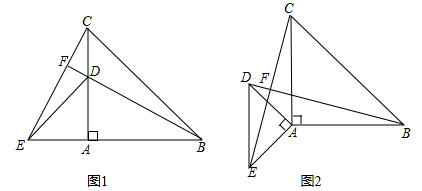 (1)、说明BD=CE;(2)、延长BD,交CE于点F,求∠BFC的度数;(3)、若如图2放置,上面的结论还成立吗?请简单说明理由.26. 已知 ,求代数式
(1)、说明BD=CE;(2)、延长BD,交CE于点F,求∠BFC的度数;(3)、若如图2放置,上面的结论还成立吗?请简单说明理由.26. 已知 ,求代数式的值,要求先化简后求值.
27. (1)、如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;(2)、如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;(3)、应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.28. 如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)、如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;(2)、如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;(3)、应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.28. 如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°. (1)、将图①中的三角板OMN沿BA方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)、将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;(3)、将图①中的三角尺COD绕点O按每秒15°的速度沿顺时针防线旋转一周,在旋转过程中,在第几秒时,MN恰好与CD平行;第几秒时,MN恰好与直线CD垂直.
(1)、将图①中的三角板OMN沿BA方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)、将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;(3)、将图①中的三角尺COD绕点O按每秒15°的速度沿顺时针防线旋转一周,在旋转过程中,在第几秒时,MN恰好与CD平行;第几秒时,MN恰好与直线CD垂直.