山东省潍坊市2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-07-03 类型:期中考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 如图所示,下列说法错误的是( )
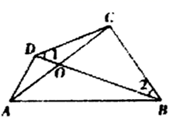 A、 也可用 表示 B、 也可用 表示 C、 也可用 表示 D、 也可用 表示3. 在方程组 、 、 、 、 中,是二元一次方程组的有( )A、2个 B、3个 C、4个 D、5个4. 下列四个图中, 与 是对顶角的是( )A、
A、 也可用 表示 B、 也可用 表示 C、 也可用 表示 D、 也可用 表示3. 在方程组 、 、 、 、 中,是二元一次方程组的有( )A、2个 B、3个 C、4个 D、5个4. 下列四个图中, 与 是对顶角的是( )A、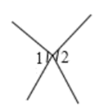 B、
B、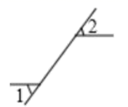 C、
C、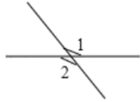 D、
D、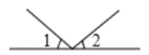 5. 如图,图中∠1与∠2是同位角的是( )
5. 如图,图中∠1与∠2是同位角的是( )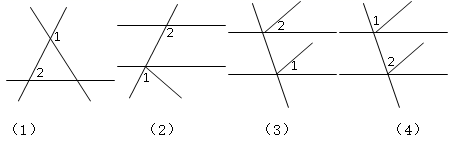 A、(2)(3) B、(2)(3)(4) C、(1)(2)(4) D、(3)(4)6. 一款智能手机的磁卡芯片直径为 米,这个数据用科学记数法表示为( )A、 B、 C、 D、7. 一个角的平分线与该角的邻补角的平分线的夹角为( )A、80° B、90° C、45° D、180°8. 如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP长不可能是( )
A、(2)(3) B、(2)(3)(4) C、(1)(2)(4) D、(3)(4)6. 一款智能手机的磁卡芯片直径为 米,这个数据用科学记数法表示为( )A、 B、 C、 D、7. 一个角的平分线与该角的邻补角的平分线的夹角为( )A、80° B、90° C、45° D、180°8. 如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP长不可能是( )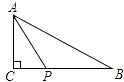 A、2.5 B、3 C、4 D、59. 计算 的结果是( )A、a B、a5 C、a6 D、a910. 如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=40°,则∠2等于( )
A、2.5 B、3 C、4 D、59. 计算 的结果是( )A、a B、a5 C、a6 D、a910. 如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=40°,则∠2等于( )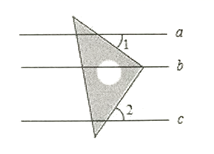 A、40° B、60° C、50° D、70°11. 若 , , ,则( )A、 B、 C、 D、12. 某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知 , , ,则 的度数是( )
A、40° B、60° C、50° D、70°11. 若 , , ,则( )A、 B、 C、 D、12. 某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知 , , ,则 的度数是( ) A、38° B、44° C、46° D、56°13. 把一张长方形纸片ABCD沿EF翻折后,点D, 分别落在 、 的位置上, 交AD于点G,则图中与 互补的角有( )
A、38° B、44° C、46° D、56°13. 把一张长方形纸片ABCD沿EF翻折后,点D, 分别落在 、 的位置上, 交AD于点G,则图中与 互补的角有( )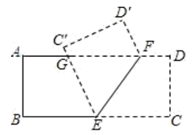 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
14. , ,15. 若2m= , 则m= .16. 在同一平面内,不重合的两条直线的位置关系有种,分别是 , .17. 如图, 已知 , , ,则
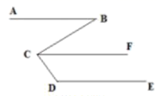 18. 如图, 直线AB、CD相交于点O, 于点O,OF平分 , ,则下列结论:① ; ② ; ③ 与 互为补角; ④ 的余角等于 ,其中正确的是(填序号)
18. 如图, 直线AB、CD相交于点O, 于点O,OF平分 , ,则下列结论:① ; ② ; ③ 与 互为补角; ④ 的余角等于 ,其中正确的是(填序号)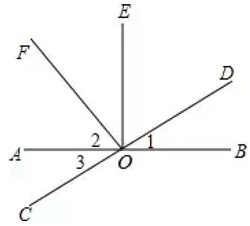 19. 新定义一种运算,其法则为 ,则
19. 新定义一种运算,其法则为 ,则三、解答题
-
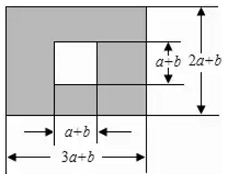
20. 计算与化简:(1)、(2)、(3)、已知 , , ,求 的值21. 解方程组:(1)、(2)、22. 如图,某市有一块长为 米,宽为 米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当 , 时的绿化面积.
 23. 推理填空:如图, , , .求 的度数.
23. 推理填空:如图, , , .求 的度数.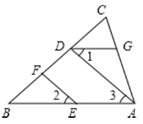
解:∵ ,
∴ ▲ ( ▲ ).
∵ ,
∴ ( ▲ ),
∴ ▲ ( ▲ ).
∴ ▲ ( ▲ ).
∵ ,
∴ ▲ .
24. 列方程(或方程组)解应用题:(1)、某服装店到厂家选购甲、乙两种服装,若购进甲种服装9件、乙种服装10件,需1810元;购进甲种服装11件乙种服装8件,需1790元,求甲乙两种服装每件价格相差多少元?(2)、某工厂现库存某种原料1200吨,用来生产A、B两种产品,每生产1吨A产品需这种原料2吨、生产费用1000元;每生产1吨B产品需这种原料2.5吨、生产费用900元,如果用来生产这两种产品的资金为53万元,那么A、B两种产品各生产多少吨才能使库存原料和资金恰好用完?25. 如图,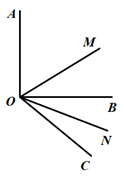 (1)、已知 是直角, , 平分 , 平分 .求 的度数;(2)、若 , 其他条件不变.求 的度数(用含 的代数式表示).26. 一般地,n个相同的因数a相乘 ,记为 ,如 ,此时,3叫做以2为底8的对数,记为 (即 ) .一般地,若 且 ,则n叫做以a为底b的对数,记为 (即 ).如 , 则4叫做以3为底81的对数,记为 (即 ).(1)、计算下列各对数的值: ; ; .(2)、观察(1)中三数4、16、64之间满足怎样的关系式, 之间又满足怎样的关系式(3)、由(2)的结果,你能归纳出一个一般性的结论吗?(4)、根据幂的运算法则: 以及对数的含义说明上述结论.
(1)、已知 是直角, , 平分 , 平分 .求 的度数;(2)、若 , 其他条件不变.求 的度数(用含 的代数式表示).26. 一般地,n个相同的因数a相乘 ,记为 ,如 ,此时,3叫做以2为底8的对数,记为 (即 ) .一般地,若 且 ,则n叫做以a为底b的对数,记为 (即 ).如 , 则4叫做以3为底81的对数,记为 (即 ).(1)、计算下列各对数的值: ; ; .(2)、观察(1)中三数4、16、64之间满足怎样的关系式, 之间又满足怎样的关系式(3)、由(2)的结果,你能归纳出一个一般性的结论吗?(4)、根据幂的运算法则: 以及对数的含义说明上述结论.