山东省泰安市岱岳区2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-07-03 类型：期中考试

进入出卷网下载

一、单选题

1. 解方程组 ${\begin{array}{l} 2 a + b = 7 ① \\ a - b = 2 ② \end{array}$ 的最佳方法是（）

A、代入法消去a,由②得 $a = b + 2$ B、代入法消去b,由①得 $b = 7 - 2 a$ C、加减法消去a,①-②×2得 $3 b = 3$ D、加减法消去b,①+②得 $3 a = 9$

查看试题解析
2. 下列命题是真命题是（）

A、两个无理数的和仍是无理数； B、垂线段最短； C、垂直于同一直线的两条直线平行； D、两直线平行，同旁内角相等；

查看试题解析
3. 如图，将一张含有 $30^{\circ}$ 角的三角形纸片的两个顶点叠放在矩形的两条对边上，若 $∠ 2 = 44^{\circ}$ ，则 $∠ 1$ 的大小为（）

A、 $14^{\circ}$ B、 $16^{\circ}$ C、 $90^{\circ} - α$ D、 $α - 44^{\circ}$

查看试题解析
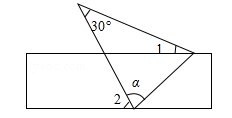4. 下列说法正确的是（）

A、任意抛掷一枚质地均匀的硬币10次，则“有5次正面朝上”是必然事件 B、明天的降水概率为40%，则“明天下雨”是确定事件 C、篮球队员在罚球线上投篮一次，则“投中”是随机事件 D、a是实数，则“|a|≥0”是不可能事件

查看试题解析
5. 如图，在4×4的方格中随机撒一颗大小忽略不计的沙粒，撒到阴影部分的概率是（）

A、 $\frac{7}{16}$ B、 $\frac{3}{8}$ C、 $\frac{3}{16}$ D、 $\frac{1}{4}$

查看试题解析
6. 足球比赛中，每场比赛都要分出胜负每队胜1场得3分，负一场扣1分，某队在8场比赛中得到12分，若设该队胜的场数为x负的场数为y，则可列方程组为（）

A、 ${\begin{array}{l} x + y = 8 \\ 3 x - y = 12 \end{array}$ B、 ${\begin{array}{l} x - y = 8 \\ 3 x - y = 12 \end{array}$ C、 ${\begin{array}{l} x + y = 18 \\ 3 x + y = 12 \end{array}$ D、 ${\begin{array}{l} x - y = 8 \\ 3 x + y = 12 \end{array}$

查看试题解析
7. 一个口袋中有红球、白球共10个，这些球除颜色外都相同，将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了100次球，发现有71次摸到红球．请你估计这个口袋中白球的数量为（）个．

A、29 B、30 C、3 D、7

查看试题解析
8. 如图，在△ABC中，∠A= $60 °$ ，∠C= $70 °$ ，BD平分∠ABC，DE∥BC，则∠BDE的度数是（）

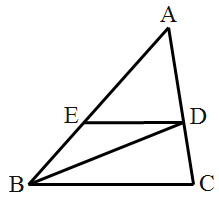A、50° B、25° C、30° D、35°

查看试题解析
9. 如图，在△ABC中，AD⊥BC ， AE平分∠BAC ，若∠BAE＝30°，∠CAD＝20°，则∠B＝（）

A、45° B、60° C、50° D、55°

查看试题解析
10. 若 $\frac{3}{4} x^{2 a + b} y^{3}$ 与 $\frac{3}{4} x^{6} y^{a - b}$ 的和是单项式，则 $a + b =$ （）

A、-3 B、0 C、3 D、6

查看试题解析
11. 一次函数y＝kx+b与y＝x+2的图象相交于如图点P（m ， 4），则关于x ， y的二元一次方程组 ${\begin{array}{l} y = k x + b \\ y = x + 2 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 4 \end{array}$ C、 ${\begin{array}{l} x = 2.4 \\ y = 4 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 4 \end{array}$

查看试题解析
12. 如图，将△ABC沿MN折叠，使MN∥BC ，点A的对应点为点A'，若∠A'＝32°，∠B＝112°，则∠A'NC的度数是（）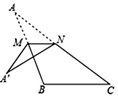

A、114° B、112° C、110° D、108°

查看试题解析

二、填空题

13. 已知实数a，b满足方程组 ${\begin{array}{l} 3 a + 2 b = 7 \\ 2 a + 3 b = 8 \end{array}$ ，则a²﹣b²的值是．

查看试题解析
14. 四个实数 $\sqrt{16}$ ， $\frac{7}{3}$ ， $\sqrt{90}$ ，π中，任取一个数是无理数的概率为．

查看试题解析
15. 如图，在 $Δ A B C$ 中， $∠ B$ 与 $∠ C$ 的平分线交于点 $P$ .若 $∠ B P C = 130 °$ ，则 $∠ A =$ ．

查看试题解析
16. 如图，AE平分∠BAC，CE平分∠ACD，要使AB∥CD，则∠1和∠2应满足的条件是．

查看试题解析
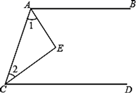17. 把定理“有两个角互余的三角形是直角三角形”，写成“如果...那么...”的形式是：如果，那么．

查看试题解析
18. 观察下面“品”字图形中各数字之间的规律，根据观察到的规律得出a+b的值为．

查看试题解析

三、解答题

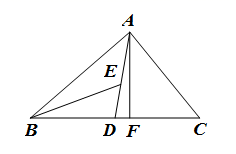
19. 如图，四边形ABCD中，AB∥DC，AB＝AD，求证：BD平分∠ADC.

查看试题解析
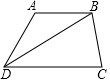20. 解下列方程组：

(1)、 ${\begin{array}{l} 3 x - y = 7 \\ 5 x + 2 y = 8 \end{array}$

(2)、 ${\begin{array}{l} 2 x + y = 13 \\ 4 x - 3 y = 11 \end{array}$ ；

(3)、 ${\begin{array}{l} \frac{x}{3} + \frac{y}{5} = 1 \\ 3 (x + y) + 2 (x - 3 y) = 15 \end{array}$ ．

查看试题解析
21. 有一盒子中装有3个白色乒乓球，2个黄色乒乓球，1个红色乒乓球，6个乒乓球除颜色外其它完全一样，李明同学从盒子中任意摸出一乒乓球．

(1)、求摸到每种颜色球的概率；

(2)、李明和王涛同学一起做游戏，李明或王涛从上述盒子中任意摸一球，如果摸到白球，李明获胜，否则王涛获胜．这个游戏对双方公平吗？说明理由．

查看试题解析
22. 如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F，∠1=∠2．

(1)、试说明：DG∥BC；

(2)、若 $∠ B = 54 °$ ， $∠ A C D = 35 °$ ，求 $∠ 3$ 的度数．

查看试题解析
23. 某一天，水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克，后再到水果市场去卖，已知猕猴桃和芒果当天的批发价和零售价如表所示：

品名

猕猴桃

芒果

批发价 $($ 元 $/$ 千克 $)$

20

40

零售价 $($ 元 $/$ 千克 $)$

26

50

(1)、他购进的猕猴桃和芒果各多少千克？

(2)、如果猕猴桃和芒果全部卖完，他能赚多少钱？

查看试题解析
24. 如图，在△ABC中，AD ， AF分别为△ABC的中线和高，BE为△ABD的角平分线．

(1)、若∠BED=40°，∠BAD=25°，求∠BAF的大小；

(2)、若△ABC的面积为40，BD=5，求AF的长．

查看试题解析
25. 暑假期间，小刚一家乘车去离家380公里的某景区旅游，他们离家的距离y（km）与汽车行驶时间x（h）之间的三段函数图象如图．

(1)、三段图像中，小刚行驶的速度最慢的是多少？

(2)、求线段AB对应的函数表达式；

(3)、小刚一家出发2.5小时时离目的地多远？

查看试题解析

品名	猕猴桃	芒果
批发价 $($ 元 $/$ 千克 $)$	20	40
零售价 $($ 元 $/$ 千克 $)$	26	50