内蒙古呼和浩特市武川县2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-07-03 类型：期中考试

进入出卷网下载

一、单选题

1. $\frac{1}{4}$ 的平方根是（）

A、 $\frac{1}{2}$ B、 $\pm \frac{1}{2}$ C、 $- \frac{1}{2}$ D、 $\pm \frac{1}{16}$

查看试题解析
2. 如图，A，B，C，D中的哪幅图案可以通过图案①平移得到（）

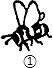A、 B、 C、 D、

查看试题解析
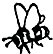3. 在平面直角坐标系中,点(-2,5)所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{9}$ ＝±3 B、 $\sqrt[3]{- 8}$ ＝﹣2 C、 $\sqrt{{(- 3)}^{2}}$ ＝﹣3 D、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$

查看试题解析
5. 在 $\frac{1}{3} ， 1.414 ， - \sqrt{2} ， π ， \sqrt[3]{8}$ 中，无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 若 $| x - 2 | + \sqrt{y + 3} = 0 ，$ 则xy的值为（）

A、-8 B、-6 C、5 D、6

查看试题解析
7. 如图，点E在BC的延长线上，下列条件中不能判定AB∥CD的是（）

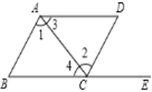A、∠1=∠2 B、∠3=∠4 C、∠B=∠DCE D、∠D+∠DAB=180°

查看试题解析
8. 20位同学在植树节这天共种了52棵树苗，其中男生每人种3棵，女生每人种2棵．设男生有x人，女生有y人，根据题意，列方程组正确的是（　　）

A、 $\{\begin{matrix} x + y = 52 \\ 3 x + 2 y = 20 \end{matrix}$ B、 $\{\begin{matrix} x + y = 52 \\ 2 x + 3 y = 20 \end{matrix}$ C、 $\{\begin{matrix} x + y = 20 \\ 2 x + 3 y = 52 \end{matrix}$ D、 $\{\begin{matrix} x + y = 20 \\ 3 x + 2 y = 52 \end{matrix}$

查看试题解析
9. 如图，现将一块三角板的含有60°角的顶点放在直尺的一边上，若∠1=2∠2，那么∠1的度数为（）

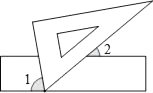A、50° B、60° C、70° D、80°

查看试题解析
10. 如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序为(1，0)、(2，0)、(2，1)、(1，1)、(1，2)、(2，2)、……，根据这个规律，第2019个点的坐标为（）

A、(45，10) B、(45，6) C、(45，22) D、(45，0)

查看试题解析

二、填空题

11. $\sqrt{81}$ 的算术平方根是， $\sqrt[3]{1 + 2 \frac{3}{8}}$ = ．

查看试题解析
12. 已知a ， b为两个连续的整数，且a< $\sqrt{57}$ <b ，则a＋b＝.

查看试题解析
13. 点P(m−1，m+3)在平面直角坐标系的y轴上，则P点坐标为.

查看试题解析
14. 如图，直线AB ， CD相交于点O ， OA平分∠EOC ， ∠EOD=120°，则∠BOD=°．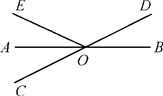

查看试题解析
15. 已知方程2x+y＝3，用含x的代数式表示y，则y＝.

查看试题解析
16. 用“*”定义新运算：对于任意实数 $a 、 b ，$ 都有 $a * b = 2 a^{2} + b ，$ 如 $3 * 4 = 2 \times 3^{2} + 4 = 22 ，$ 那么 $\sqrt{3} * 2 =$ .

查看试题解析

三、解答题

17. 计算

(1)、 $| - \sqrt{9} | + \sqrt[3]{- 8} - \sqrt{\frac{1}{4}}$

(2)、 ${(x - 1)}^{2} = \frac{1}{4}$

(3)、 $\sqrt{{(- 2)}^{2}} + | \sqrt{2} - 1 | - (\sqrt{2} + 1)$

(4)、 $3 {(x - 4)}^{3} = - 375$

查看试题解析
18. 解方程：

(1)、 ${\begin{matrix} x - y = 3 \\ 4 x + y = 2 \end{matrix}$

(2)、 ${\begin{matrix} x + y = 10 \\ 2 x + y = 16 \end{matrix}$

查看试题解析
19. 如图，AD∥BE，∠1=∠2，求证：∠A=∠E.

请完成解答过程：

解：∵AD∥BE(已知)

∠A=∠()

又∵1=∠2(已知)

∴AC∥()

∴∠3=∠(两直线平行，内错角相等)

∴∠A=∠E()

查看试题解析
20. 若5a+1和a﹣19是数m的平方根．求a和m的值．

查看试题解析
21. 已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A(0，3)，B(3，4)，C(2，2)(正方形网格中每个小正方形的边长是一个单位长度)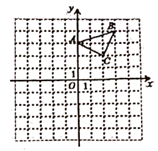

(1)、画出△ABC向下平移4个单位长度得到的△A₁B₁C₁；

(2)、求△A₁B₁C₁的面积．

查看试题解析
22. “鸡兔同笼”是我国古代著名的数学趣题之一．大约在1500年前成书的《孙子算经》中，就有关于“鸡兔同笼”的记载：“今有雏兔同笼，上有二十五头，下有七十六足，问雏兔各几何？”这四句话的意思是：有若干只鸡兔关在一个笼子里，从上面数，有25个头；从下面数，有76条腿，问笼中各有几只鸡和兔？

查看试题解析
23. 如图，∠1=80°，∠2=100°∠C=∠D.

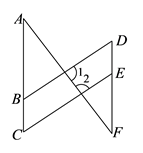(1)、判断AC与DF的位置关系，并说明理由；

(2)、若∠C比∠A大20°，求∠F的度数.

查看试题解析
24. 如图，已知∠ABC．点D为∠ABC的内部一点，请你再画一个∠DEF，使DE∥AB，EF∥BC，且DE交BC边与点P

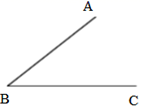(1)、操作：画出满足题意的图形.

(2)、探究：根据所画图形猜想∠ABC与∠DEF有怎样的数量关系?并说明理由.

查看试题解析
25. 如图，平面直角坐标系中，ABCD为长方形，其中点A、C坐标分别为（﹣8，4）、（2，﹣8），且AD∥x轴，交y轴于M点，AB交x轴于N．

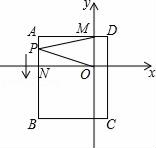(1)、求B、D两点坐标和长方形ABCD的面积；

(2)、一动点P从A出发（不与A点重合），以 $\frac{1}{2}$ 个单位/秒的速度沿AB向B点运动，在P点运动过程中，连接MP、OP，请直接写出∠AMP、∠MPO、∠PON之间的数量关系；

(3)、是否存在某一时刻t，使三角形AMP的面积等于长方形面积的 $\frac{1}{3}$ ？若存在，求t的值并求此时点P的坐标；若不存在请说明理由．

查看试题解析