江西省赣州市2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期：2020-07-03 类型：期中考试
一、单选题
-
1. 下列几组图形中，通过平移后能够重合的是（ ）A、
B、
C、
D、
2. 9的算术平方根是( )A、3 B、±3 C、 D、±3. 如图把一个长方形纸片，沿EF折叠后，点D，C分别落在D'，C'的位置，若∠EFB= ，则∠AED'的度数为（ ）
A、30° B、53° C、40° D、45°4.如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“马”的坐标为（1，﹣1），则棋子“炮”的坐标为（ ）
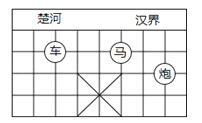A、（3，2） B、（﹣3，2） C、（3，﹣2） D、（﹣3，﹣2）5. 若a、b均为正整数，且a＞ ， b＞ ， 则a+b的最小值是（ ）A、6 B、7 C、8 D、96. 如图，∠1和∠2为同位角的是（ ）A、
B、
C、
D、
二、填空题
-
7. 剧院里5排2号可以用(5，2)表示，则(9，6)表示.8. 把命题“同位角相等”改写成“如果……那么……”的形式：9. 若将 向右平移2个单位长度后，再向上平移1个单位长度得到点 ，则点 的实际坐标是 ．10. 如图，直线AB、CD与直线EF相交于E、F， ，当 时，能使AB//CD．
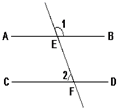11. 已知线段AB与直线CD互相垂直，垂足为点O，且AO=5cm，BO=3cm，则线段AB的长为 ．12. 已知 =4， 3，且 ，则 的值为 ．三、解答题
-
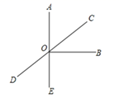
13. 计算(1)、(2)、14. 如图，已知直线AE，CD相交于点O，且∠AOB= ，∠BOC= ，求∠DOE，∠AOD的度数
15. 求下列各式中x的值．(1)、(2)、16. 下图是某市的部分简图，为了确定各建筑物的位置：
(1)、请你以火车站为原点建立平面直角坐标系(2)、分别写出市场、超市、体育场的坐标（小正方形网格的单位长度为1）．17. 如图，MF⊥NF于F，MF交AB于点E，NF交CD于点G，∠1=140°，∠2=50°，试判断AB和CD的位置关系，并说明理由．
18. 把下列各数分别填入相应的集合中(1)、整数集合：｛｝(2)、分数集合：｛｝(3)、有理数集合：｛｝(4)、无理数集合：｛｝19. 如图，已知DE∥BC ， CD是∠ACB的平分线，∠B＝70°，∠ACB＝50°，求∠EDC和∠AED的度数．
20. 某小区有一块面积为196m2的正方形空地，开发商计划在此空地上建一个面积为100m2的长方形花坛，使长方形的长是宽的2倍．请你通过计算说明开发商能否实现这个愿望？（参考数据： ≈1.414， ≈7.070）21. △ABC与△A′B′C′在平面直角坐标系中的位置如图．
(1)、分别写出下列各点的坐标：A；B′；C′；(2)、若点P（a ， b）是△ABC内部一点，则平移后△A′B′C′内的对应点P′的坐标为；(3)、求△ABC的面积．22. 如图所示，MN，EF是两面互相平行的镜面，根据镜面反射规律，若一束光线AB照射到镜面MN上，反射光线为BC，则一定有∠1=∠2.试根据这一规律：
(1)、利用直尺和量角器作出光线BC经镜面EF反射后的反射光线CD；(2)、试判断AB与CD的位置关系，并说明理由.23. 如图，在平面直角坐标系中，点A，B的坐标分别是(-2，0)，(4，0)，现同时将点A，B分别向上平移2个单位长度，再向右平移2个单位长度，得到A，B的对应点C，D连接AC，BD，CD.
(1)、写出点C，D的坐标并求出四边形ABCD的面积.(2)、在x轴上是否存在一点E，使得 的面积是 面积的2倍？若存在，请求出E 的坐标；若不存在，请说明理由.(3)、若点F是直线BD上一个动点，连接FC，FO，当点F在直线BD上运动时，请直接写出 与 的数量关系.